As complement to the accepted answer, I will answer the following questions
- What is the interpretation of MSE loss and cross entropy loss from probability perspective?
- Why cross entropy is used for classification and MSE is used for linear regression?
TL;DR Use MSE loss if (random) target variable is from Gaussian distribution and categorical cross entropy loss if (random) target variable is from Multinomial distribution.
MSE (Mean squared error)
One of the assumptions of the linear regression is multi-variant normality. From this it follows that the target variable is normally distributed(more on the assumptions of linear regression can be found here and here).
Gaussian distribution(Normal distribution) with mean 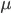 and variance
and variance 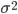 is given by
is given by
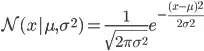
Often in machine learning we deal with distribution with mean 0 and variance 1(Or we transform our data to have mean 0 and variance 1). In this case the normal distribution will be,
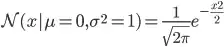 This is called standard normal distribution.
This is called standard normal distribution.
For normal distribution model with weight parameter 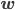 and precision(inverse variance) parameter
and precision(inverse variance) parameter 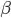 , the probability of observing a single target
, the probability of observing a single target t given input x is expressed by the following equation
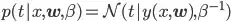 , where
, where 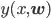 is mean of the distribution and is calculated by model as
is mean of the distribution and is calculated by model as
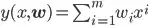
Now the probability of target vector 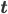 given input
given input 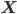 can be expressed by
can be expressed by
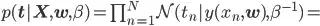
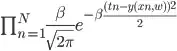
Taking natural logarithm of left and right terms yields
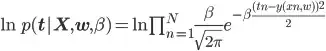
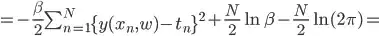
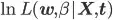
Where 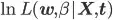 is log likelihood of normal function. Often training a model involves optimizing the likelihood function with respect to
is log likelihood of normal function. Often training a model involves optimizing the likelihood function with respect to 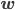 . Now maximum likelihood function for parameter
. Now maximum likelihood function for parameter 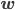 is given by (constant terms with respect to
is given by (constant terms with respect to 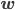 can be omitted),
can be omitted),
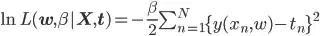
For training the model omitting the constant 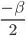 doesn't affect the convergence.
doesn't affect the convergence.
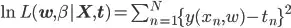 This is called squared error and taking the
This is called squared error and taking the mean yields mean squared error.
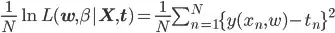 ,
,
Cross entropy
Before going into more general cross entropy function, I will explain specific type of cross entropy - binary cross entropy.
Binary Cross entropy
The assumption of binary cross entropy is probability distribution of target variable is drawn from Bernoulli distribution. According to Wikipedia
Bernoulli distribution is the discrete probability distribution of a random variable which
takes the value 1 with probability p and the value 0
with probability q=1-p
Probability of Bernoulli distribution random variable is given by
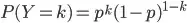 , where
, where  and p is probability of success.
This can be simply written as
and p is probability of success.
This can be simply written as
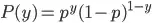
Taking negative natural logarithm of both sides yields
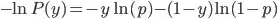 , this is called binary cross entropy.
, this is called binary cross entropy.
Categorical cross entropy
Generalization of the cross entropy follows the general case
when the random variable is multi-variant(is from Multinomial distribution
) with the following probability distribution

Taking negative natural logarithm of both sides yields categorical cross entropy loss.
 ,
,

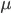 and variance
and variance 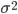 is given by
is given by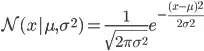
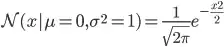 This is called standard normal distribution.
This is called standard normal distribution.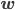 and precision(inverse variance) parameter
and precision(inverse variance) parameter 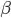 , the probability of observing a single target
, the probability of observing a single target 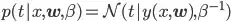 , where
, where 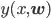 is mean of the distribution and is calculated by model as
is mean of the distribution and is calculated by model as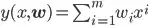
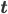 given input
given input 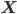 can be expressed by
can be expressed by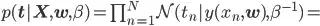
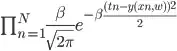
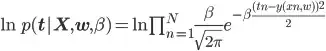
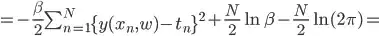
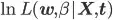
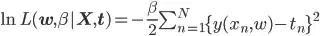
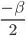 doesn't affect the convergence.
doesn't affect the convergence.
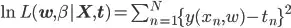 This is called squared error and taking the
This is called squared error and taking the 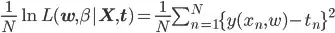 ,
,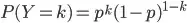 , where
, where  and p is probability of success.
This can be simply written as
and p is probability of success.
This can be simply written as
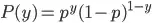
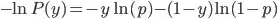 , this is called binary cross entropy.
, this is called binary cross entropy.
 ,
,