Discrete probability distribution plot with given values

Question

First of all, I could not draw the graphics myself. Because, unfortunately I have no computer and mathematical software.. I do not know how to use these softwares.

I need to create a discrete probabilistic distribution plot of the following values.

I tried Wolfram Alpha (as an online software), but it is impossible to do so because the number of values ​​is so long.

EXAMPLE:

I would like to set up a graph similar to the graphs of the following distribution functions:

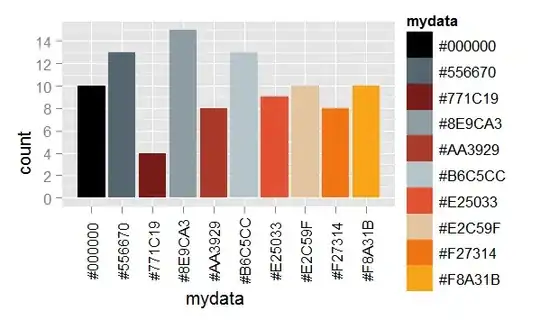
P_1(x)={ 3/42,3/42,4/42,3/42,4/42,5/42,3/42,3/42,1/42,2/42,2/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,0/42,1/42,1/42,2/42,2/42,2/42,1/42}

P_2(x)={ 4/170,6/170,8/170,6/170,8/170,11/170,8/170,9/170,6/170,6/170,8/170,4/170,7/170,3/170,5/170,3/170,3/170,3/170,0/170,1/170,0/170,1/170,2/170,2/170,1/170,0/170,1/170,1/170,1/170,2/170,2/170,2/170,2/170,2/170,2/170,2/170,3/170,3/170,4/170,5/170,4/170,6/170,4/170,4/170,1/170,2/170,1/170,0/170,0/170,0/170,0/170,1/170}

P_3(x)={ 5/682,9/682,13/682,15/682,20/682,25/682,25/682,34/682,21/682,26/682,24/682,21/682,26/682,19/682,21/682,22/682,14/682,20/682,10/682,13/682,10/682,6/682,11/682,6/682,8/682,3/682,4/682,5/682,5/682,8/682,5/682,9/682,7/682,9/682,10/682,5/682,5/682,5/682,7/682,11/682,11/682,15/682,13/682,16/682,11/682,15/682,18/682,9/682,9/682,3/682,6/682,10/682,5/682,4/682,2/682,2/682,1/682,0/682,1/682,0/682,2/682,1/682,1/682,3/682,1/682,1/682}

P_4(x)={ 6/2730,12/2730,22/2730,28/2730,41/2730,55/2730,58/2730,80/2730,68/2730,91/2730,84/2730,72/2730,87/2730,65/2730,82/2730,89/2730,61/2730,80/2730,51/2730,66/2730,49/2730,47/2730,61/2730,39/2730,50/2730,21/2730,31/2730,34/2730,24/2730,40/2730,23/2730,36/2730,34/2730,31/2730,44/2730,27/2730,33/2730,18/2730,25/2730,37/2730,33/2730,50/2730,35/2730,52/2730,40/2730,52/2730,66/2730,45/2730,48/2730,32/2730,34/2730,43/2730,32/2730,37/2730,22/2730,29/2730,21/2730,15/2730,22/2730,10/2730,18/2730,11/2730,15/2730,22/2730,10/2730,13/2730,1/2730,4/2730,4/2730,1/2730,2/2730,1/2730,2/2730,0/2730,1/2730,2/2730,0/2730,1/2730,1/2730,0/2730,0/2730,0/2730,0/2730,0/2730,0/2730,0/2730,1/2730}

P_5(x)={ 7/10922,17/10922,33/10922,47/10922,77/10922,108/10922,126/10922,179/10922,167/10922,226/10922,245/10922,235/10922,308/10922,224/10922,303/10922,300/10922,263/10922,318/10922,216/10922,278/10922,204/10922,238/10922,282/10922,180/10922,229/10922,138/10922,185/10922,211/10922,145/10922,194/10922,122/10922,168/10922,137/10922,136/10922,168/10922,113/10922,150/10922,93/10922,123/10922,132/10922,118/10922,165/10922,124/10922,174/10922,156/10922,167/10922,215/10922,150/10922,204/10922,134/10922,167/10922,208/10922,127/10922,180/10922,107/10922,145/10922,119/10922,97/10922,131/10922,81/10922,100/10922,63/10922,78/10922,99/10922,61/10922,83/10922,43/10922,56/10922,58/10922,35/10922,46/10922,19/10922,26/10922,13/10922,14/10922,18/10922,7/10922,8/10922,4/10922,8/10922,9/10922,3/10922,6/10922,2/10922,6/10922,4/10922,6/10922,11/10922,5/10922,6/10922,2/10922,3/10922,6/10922,2/10922,4/10922,4/10922,2/10922,1/10922,2/10922,2/10922,1/10922,2/10922}

P_6(x)={ 8/43690,22/43690,48/43690,77/43690,133/43690,196/43690,262/43690,391/43690,396/43690,550/43690,607/43690,656/43690,877/43690,689/43690,919/43690,922/43690,904/43690,1104/43690,823/43690,1058/43690,806/43690,919/43690,1120/43690,792/43690,1028/43690,647/43690,876/43690,930/43690,721/43690,876/43690,585/43690,741/43690,621/43690,615/43690,777/43690,528/43690,695/43690,420/43690,544/43690,608/43690,488/43690,656/43690,458/43690,620/43690,588/43690,591/43690,775/43690,545/43690,761/43690,507/43690,666/43690,818/43690,551/43690,735/43690,466/43690,626/43690,560/43690,505/43690,659/43690,387/43690,509/43690,307/43690,401/43690,541/43690,314/43690,438/43690,259/43690,339/43690,361/43690,234/43690,318/43690,154/43690,214/43690,125/43690,161/43690,196/43690,90/43690,125/43690,61/43690,95/43690,114/43690,58/43690,88/43690,39/43690,65/43690,36/43690,43/43690,72/43690,41/43690,49/43690,28/43690,41/43690,50/43690,27/43690,32/43690,16/43690,25/43690,12/43690,20/43690,28/43690,11/43690,13/43690,6/43690,9/43690,13/43690,2/43690,6/43690,2/43690,2/43690,3/43690,3/43690,10/43690,3/43690,7/43690,2/43690,3/43690,4/43690,2/43690,4/43690,0/43690,1/43690,1/43690,1/43690,1/43690,1/43690,0/43690,0/43690,0/43690,1/43690}

P_7(x)={ 9/174762,27/174762,67/174762,118/174762,220/174762,348/174762,486/174762,771/174762,825/174762,1214/174762,1373/174762,1633/174762,2257/174762,1906/174762,2554/174762,2557/174762,2737/174762,3353/174762,2728/174762,3572/174762,2798/174762,3278/174762,3935/174762,3040/174762,3969/174762,2675/174762,3469/174762,3713/174762,2907/174762,3630/174762,2491/174762,3269/174762,2647/174762,2733/174762,3408/174762,2315/174762,3043/174762,1931/174762,2584/174762,2710/174762,2155/174762,2789/174762,1904/174762,2566/174762,2473/174762,2331/174762,3061/174762,2134/174762,2871/174762,1939/174762,2595/174762,3186/174762,2249/174762,3031/174762,1967/174762,2575/174762,2440/174762,2253/174762,2909/174762,1827/174762,2398/174762,1549/174762,1992/174762,2595/174762,1593/174762,2098/174762,1248/174762,1661/174762,1819/174762,1347/174762,1741/174762,991/174762,1320/174762,792/174762,964/174762,1310/174762,710/174762,939/174762,507/174762,694/174762,826/174762,473/174762,651/174762,341/174762,468/174762,264/174762,328/174762,494/174762,253/174762,357/174762,179/174762,263/174762,348/174762,180/174762,273/174762,130/174762,193/174762,133/174762,157/174762,209/174762,100/174762,138/174762,63/174762,91/174762,130/174762,58/174762,79/174762,40/174762,67/174762,58/174762,53/174762,77/174762,40/174762,53/174762,24/174762,32/174762,48/174762,22/174762,35/174762,20/174762,25/174762,28/174762,14/174762,17/174762,11/174762,15/174762,5/174762,8/174762,17/174762,7/174762,8/174762,2/174762,2/174762,4/174762,4/174762,8/174762,2/174762,2/174762,0/174762,1/174762,3/174762,1/174762,3/174762,0/174762,0/174762,0/174762,0/174762,0/174762,0/174762,2/174762,0/174762,0/174762,0/174762,0/174762,0/174762,0/174762,0/174762,0/174762,0/174762,0/174762,0/174762,0/174762,1/174762,1/174762}

P_8(x)={ 10/699050,34/699050,90/699050,176/699050,350/699050,577/699050,871/699050,1436/699050,1657/699050,2534/699050,2966/699050,3764/699050,5358/699050,4882/699050,6698/699050,6791/699050,7702/699050,9604/699050,8231/699050,10947/699050,8918/699050,10913/699050,12958/699050,10509/699050,13828/699050,9786/699050,12794/699050,13566/699050,11358/699050,14039/699050,9970/699050,13110/699050,10714/699050,11362/699050,14112/699050,9696/699050,12748/699050,8299/699050,10977/699050,11669/699050,9297/699050,11941/699050,8009/699050,10755/699050,10446/699050,9502/699050,12403/699050,8392/699050,11276/699050,7651/699050,10182/699050,12325/699050,9126/699050,12174/699050,8067/699050,10627/699050,10042/699050,9292/699050,12137/699050,7975/699050,10516/699050,6945/699050,8760/699050,11373/699050,7282/699050,9587/699050,5943/699050,7862/699050,8529/699050,6461/699050,8474/699050,5139/699050,6852/699050,4337/699050,5341/699050,6935/699050,4055/699050,5350/699050,3019/699050,4024/699050,4776/699050,3023/699050,4058/699050,2251/699050,3039/699050,1851/699050,2247/699050,3039/699050,1720/699050,2289/699050,1249/699050,1742/699050,2273/699050,1290/699050,1830/699050,987/699050,1372/699050,972/699050,978/699050,1372/699050,767/699050,1038/699050,538/699050,722/699050,994/699050,529/699050,710/699050,367/699050,535/699050,509/699050,393/699050,589/699050,316/699050,401/699050,226/699050,297/699050,389/699050,197/699050,290/699050,143/699050,202/699050,226/699050,147/699050,211/699050,103/699050,140/699050,79/699050,101/699050,142/699050,67/699050,106/699050,51/699050,67/699050,75/699050,46/699050,65/699050,32/699050,45/699050,36/699050,42/699050,55/699050,24/699050,34/699050,11/699050,12/699050,25/699050,9/699050,21/699050,8/699050,17/699050,10/699050,9/699050,11/699050,5/699050,14/699050,5/699050,7/699050,6/699050,3/699050,7/699050,4/699050,5/699050,7/699050,6/699050,6/699050,3/699050,2/699050,0/699050,1/699050,2/699050,0/699050,2/699050,2/699050,3/699050,2/699050,2/699050,0/699050,0/699050,0/699050,0/699050,1/699050,1/699050,0/699050,0/699050,0/699050,1/699050,2/699050,1/699050,2/699050,0/699050,0/699050,0/699050,0/699050,1/699050,1/699050,2/699050}

P_9(x)={ 11/2796202,41/2796202,118/2796202,251/2796202,532/2796202,924/2796202,1500/2796202,2580/2796202,3164/2796202,5018/2796202,6108/2796202,8193/2796202,12030/2796202,11599/2796202,16410/2796202,16947/2796202,20329/2796202,25638/2796202,23361/2796202,31525/2796202,26494/2796202,33543/2796202,39633/2796202,33833/2796202,44866/2796202,33020/2796202,43543/2796202,45974/2796202,41030/2796202,50612/2796202,37388/2796202,49151/2796202,40472/2796202,44081/2796202,54221/2796202,38847/2796202,51156/2796202,33921/2796202,44680/2796202,48127/2796202,38710/2796202,48902/2796202,33436/2796202,44407/2796202,43373/2796202,39062/2796202,50116/2796202,34268/2796202,45652/2796202,30338/2796202,40610/2796202,47920/2796202,36278/2796202,48435/2796202,32356/2796202,42939/2796202,41366/2796202,37675/2796202,49334/2796202,33062/2796202,43626/2796202,29838/2796202,37507/2796202,48140/2796202,31771/2796202,42095/2796202,26739/2796202,35539/2796202,37571/2796202,29438/2796202,38388/2796202,24218/2796202,32092/2796202,21490/2796202,26087/2796202,33871/2796202,20799/2796202,27405/2796202,16238/2796202,21484/2796202,25225/2796202,16608/2796202,22120/2796202,12875/2796202,17174/2796202,10980/2796202,13179/2796202,17537/2796202,10097/2796202,13580/2796202,7732/2796202,10423/2796202,13393/2796202,7912/2796202,10700/2796202,6146/2796202,8242/2796202,6077/2796202,6224/2796202,8464/2796202,4728/2796202,6495/2796202,3578/2796202,4873/2796202,6457/2796202,3565/2796202,4909/2796202,2640/2796202,3644/2796202,3535/2796202,2742/2796202,3829/2796202,2090/2796202,2847/2796202,1587/2796202,2128/2796202,2914/2796202,1549/2796202,2116/2796202,1147/2796202,1600/2796202,1751/2796202,1134/2796202,1596/2796202,838/2796202,1190/2796202,645/2796202,836/2796202,1169/2796202,600/2796202,853/2796202,452/2796202,668/2796202,780/2796202,409/2796202,581/2796202,292/2796202,423/2796202,278/2796202,324/2796202,474/2796202,242/2796202,334/2796202,158/2796202,234/2796202,327/2796202,166/2796202,234/2796202,114/2796202,165/2796202,110/2796202,107/2796202,171/2796202,84/2796202,138/2796202,66/2796202,86/2796202,114/2796202,56/2796202,78/2796202,41/2796202,57/2796202,70/2796202,49/2796202,63/2796202,26/2796202,49/2796202,25/2796202,36/2796202,51/2796202,14/2796202,22/2796202,12/2796202,18/2796202,23/2796202,20/2796202,20/2796202,6/2796202,11/2796202,4/2796202,10/2796202,15/2796202,9/2796202,10/2796202,5/2796202,8/2796202,11/2796202,6/2796202,10/2796202,6/2796202,9/2796202,5/2796202,8/2796202,14/2796202,7/2796202,14/2796202,7/2796202,7/2796202,5/2796202,1/2796202,5/2796202,1/2796202,2/2796202,4/2796202,1/2796202,3/2796202,3/2796202,3/2796202,1/2796202,3/2796202,3/2796202,0/2796202,1/2796202,0/2796202,0/2796202,1/2796202,1/2796202,1/2796202,0/2796202,0/2796202,0/2796202,1/2796202}

Where, x={1,2,3,4,5,.....{up to the number of given values}

In fact this question is a mathematical question: What mathematical functions do these probabilistic distributions simulate? But since I can not make graphics, I can not answer..I just need help to create graphics.

Endless thanks for any help..

A sample drawing I need:

Answer 1

[Complete reedit] after OP edit putting more graphs to single SVG

Well than you can use SVG for the graph (you just need text editor and SVG viewer like Internet browser). You just need a slight modification of the data and either script or manual construct the SVG path. Compute common scale and adjust transform of each graph/path accordingly. Here is VCL/C++ script for this (can ignore the VCL stuff I only use AnsiString type for text manipulation and Memo for simple save of the text to file):

//---------------------------------------------------------------------------
AnsiString generate_svg(int *P)
    {
    AnsiString svg,path;
    float xm,ym,dm,f; int i,ix,c,d,x,y;
    const AnsiString col[]=
        {
        "aliceblue"           ,
        "antiquewhite"        ,
        "aqua"                ,
        "aquamarine"          ,
        "azure"               ,
        "beige"               ,
        "bisque"              ,
        "black"               ,
        "blanchedalmond"      ,
        "blue"                ,
        "blueviolet"          ,
        "brown"               ,
        "burlywood"           ,
        "cadetblue"           ,
        "chartreuse"          ,
        "chocolate"           ,
        "coral"               ,
        "lightpink"           ,
        "lightsalmon"         ,
        "lightseagreen"       ,
        "lightskyblue"        ,
        "lightslategray"      ,
        "lightslategrey"      ,
        "lightsteelblue"      ,
        "lightyellow"         ,
        "lime"                ,
        "limegreen"           ,
        "linen"               ,
        "magenta"             ,
        "maroon"              ,
        "mediumaquamarine"    ,
        "mediumblue"          ,
        "mediumorchid"        ,
        "cornflowerblue"      ,
        "cornsilk"            ,
        "crimson"             ,
        "cyan"                ,
        "darkblue"            ,
        "darkcyan"            ,
        "darkgoldenrod"       ,
        "darkgray"            ,
        "darkgreen"           ,
        "darkgrey"            ,
        "darkkhaki"           ,
        "darkmagenta"         ,
        "darkolivegreen"      ,
        "darkorange"          ,
        "darkorchid"          ,
        "darkred"             ,
        "darksalmon"          ,
        "darkseagreen"        ,
        "darkslateblue"       ,
        "darkslategray"       ,
        "darkslategrey"       ,
        "darkturquoise"       ,
        "darkviolet"          ,
        "deeppink"            ,
        "deepskyblue"         ,
        "dimgray"             ,
        "dimgrey"             ,
        "dodgerblue"          ,
        "firebrick"           ,
        "floralwhite"         ,
        "forestgreen"         ,
        "fuchsia"             ,
        "gainsboro"           ,
        "ghostwhite"          ,
        "gold"                ,
        "goldenrod"           ,
        "gray"                ,
        "grey"                ,
        "green"               ,
        "greenyellow"         ,
        "honeydew"            ,
        "hotpink"             ,
        "indianred"           ,
        "indigo"              ,
        "ivory"               ,
        "khaki"               ,
        "lavender"            ,
        "lavenderblush"       ,
        "mediumpurple"        ,
        "mediumseagreen"      ,
        "mediumslateblue"     ,
        "mediumspringgreen"   ,
        "mediumturquoise"     ,
        "mediumvioletred"     ,
        "midnightblue"        ,
        "mintcream"           ,
        "mistyrose"           ,
        "moccasin"            ,
        "navajowhite"         ,
        "navy"                ,
        "oldlace"             ,
        "olive"               ,
        "olivedrab"           ,
        "orange"              ,
        "orangered"           ,
        "orchid"              ,
        "palegoldenrod"       ,
        "palegreen"           ,
        "paleturquoise"       ,
        "palevioletred"       ,
        "papayawhip"          ,
        "peachpuff"           ,
        "peru"                ,
        "pink"                ,
        "plum"                ,
        "powderblue"          ,
        "purple"              ,
        "red"                 ,
        "rosybrown"           ,
        "royalblue"           ,
        "saddlebrown"         ,
        "salmon"              ,
        "sandybrown"          ,
        "seagreen"            ,
        "seashell"            ,
        "sienna"              ,
        "silver"              ,
        "skyblue"             ,
        "slateblue"           ,
        "slategray"           ,
        "slategrey"           ,
        "snow"                ,
        "springgreen"         ,
        "steelblue"           ,
        "tan"                 ,
        "teal"                ,
        "lawngreen"           ,
        "lemonchiffon"        ,
        "lightblue"           ,
        "lightcoral"          ,
        "lightcyan"           ,
        "lightgoldenrodyellow",
        "lightgray"           ,
        "lightgreen"          ,
        "lightgrey"           ,
        "thistle"             ,
        "tomato"              ,
        "turquoise"           ,
        "violet"              ,
        "wheat"               ,
        "white"               ,
        "whitesmoke"          ,
        "yellow"              ,
        "yellowgreen"         ,
        };

    // find max x,y,d (for computation of global transform)
    for (xm=0,ym=0,dm=0,i=0,ix=0;P[i]>=0;ix++,i++)  // process all graphs in P[]
        {
        d=P[i]; i++;            // divider
        if (dm<d) dm=d;         // global max divider
        for (x=0,y=0;P[i]>=0;i++,x++)   // process single graph
         if (y<P[i]) y=P[i];    // local max y
        f=float(y)/float(d);
        if (ym<f) ym=f;         // global max y
        if (xm<x) xm=x;         // global max x
        }
    // [SVG header]
    svg ="<svg xmlns=\"http://www.w3.org/2000/svg\" viewBox=\"-100 -100 1100 1100\">\r\n";
    // [support gfx] <0,1000> coordinates
    svg+=" <g fill=\"none\" stroke-width=\"1px\">\r\n";
    svg+="  <rect stroke=\"black\" x=\"0\" y=\"0\" height=\"1000\" width=\"1000\"/>\r\n";
    // [graphs]
    for (i=0,ix=0;P[i]>=0;ix++,i++) // process all graphs in P[]
        {
        f=P[i]; i++;            // divider
        f*=2.0*ym;              // scale
        svg+="  <path stroke=\""+col[ix]+"\"";
        svg+=AnsiString().sprintf(" transform=\"matrix(%.6f,%.6f,%.6f,%.6f,%.6f,%.6f)\"",1000.0/xm,0.0,0.0,-1000.0/f,0.0,1000.0);
        svg+=" d=\"M 0 0"; // Move to (0,0) absolute
        for (x=0;P[i]>=0;i++,x++)   // process single graph
         svg+=AnsiString().sprintf(" L %i %i",x,P[i]); // Line to (x,y) absolute
        svg+="\"/>\r\n";
        }
    svg+=" </g>\r\n";
    svg+="</svg>\r\n";
    return svg;
    }
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner):TForm(Owner)
    {
    int P[]=
        {
    //  divider,y0,y1,y2,....,-1
             42,3,3,4,3,4,5,3,3,1,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,2,2,2,1,-1,
            170,4,6,8,6,8,11,8,9,6,6,8,4,7,3,5,3,3,3,0,1,0,1,2,2,1,0,1,1,1,2,2,2,2,2,2,2,3,3,4,5,4,6,4,4,1,2,1,0,0,0,0,1,-1,
             682,5,9,13,15,20,25,25,34,21,26,24,21,26,19,21,22,14,20,10,13,10,6,11,6,8,3,4,5,5,8,5,9,7,9,10,5,5,5,7,11,11,15,13,16,11,15,18,9,9,3,6,10,5,4,2,2,1,0,1,0,2,1,1,3,1,1,-1,
           2730,6,12,22,28,41,55,58,80,68,91,84,72,87,65,82,89,61,80,51,66,49,47,61,39,50,21,31,34,24,40,23,36,34,31,44,27,33,18,25,37,33,50,35,52,40,52,66,45,48,32,34,43,32,37,22,29,21,15,22,10,18,11,15,22,10,13,1,4,4,1,2,1,2,0,1,2,0,1,1,0,0,0,0,0,0,0,1,-1,
          10922,7,17,33,47,77,108,126,179,167,226,245,235,308,224,303,300,263,318,216,278,204,238,282,180,229,138,185,211,145,194,122,168,137,136,168,113,150,93,123,132,118,165,124,174,156,167,215,150,204,134,167,208,127,180,107,145,119,97,131,81,100,63,78,99,61,83,43,56,58,35,46,19,26,13,14,18,7,8,4,8,9,3,6,2,6,4,6,11,5,6,2,3,6,2,4,4,2,1,2,2,1,2,-1,
          43690,8,22,48,77,133,196,262,391,396,550,607,656,877,689,919,922,904,1104,823,1058,806,919,1120,792,1028,647,876,930,721,876,585,741,621,615,777,528,695,420,544,608,488,656,458,620,588,591,775,545,761,507,666,818,551,735,466,626,560,505,659,387,509,307,401,541,314,438,259,339,361,234,318,154,214,125,161,196,90,125,61,95,114,58,88,39,65,36,43,72,41,49,28,41,50,27,32,16,25,12,20,28,11,13,6,9,13,2,6,2,2,3,3,10,3,7,2,3,4,2,4,0,1,1,1,1,1,0,0,0,1,-1,
         174762,9,27,67,118,220,348,486,771,825,1214,1373,1633,2257,1906,2554,2557,2737,3353,2728,3572,2798,3278,3935,3040,3969,2675,3469,3713,2907,3630,2491,3269,2647,2733,3408,2315,3043,1931,2584,2710,2155,2789,1904,2566,2473,2331,3061,2134,2871,1939,2595,3186,2249,3031,1967,2575,2440,2253,2909,1827,2398,1549,1992,2595,1593,2098,1248,1661,1819,1347,1741,991,1320,792,964,1310,710,939,507,694,826,473,651,341,468,264,328,494,253,357,179,263,348,180,273,130,193,133,157,209,100,138,63,91,130,58,79,40,67,58,53,77,40,53,24,32,48,22,35,20,25,28,14,17,11,15,5,8,17,7,8,2,2,4,4,8,2,2,0,1,3,1,3,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0,0,1,1,-1,
         699050,10,34,90,176,350,577,871,1436,1657,2534,2966,3764,5358,4882,6698,6791,7702,9604,8231,10947,8918,10913,12958,10509,13828,9786,12794,13566,11358,14039,9970,13110,10714,11362,14112,9696,12748,8299,10977,11669,9297,11941,8009,10755,10446,9502,12403,8392,11276,7651,10182,12325,9126,12174,8067,10627,10042,9292,12137,7975,10516,6945,8760,11373,7282,9587,5943,7862,8529,6461,8474,5139,6852,4337,5341,6935,4055,5350,3019,4024,4776,3023,4058,2251,3039,1851,2247,3039,1720,2289,1249,1742,2273,1290,1830,987,1372,972,978,1372,767,1038,538,722,994,529,710,367,535,509,393,589,316,401,226,297,389,197,290,143,202,226,147,211,103,140,79,101,142,67,106,51,67,75,46,65,32,45,36,42,55,24,34,11,12,25,9,21,8,17,10,9,11,5,14,5,7,6,3,7,4,5,7,6,6,3,2,0,1,2,0,2,2,3,2,2,0,0,0,0,1,1,0,0,0,1,2,1,2,0,0,0,0,1,1,2,-1,
        2796202,11,41,118,251,532,924,1500,2580,3164,5018,6108,8193,12030,11599,16410,16947,20329,25638,23361,31525,26494,33543,39633,33833,44866,33020,43543,45974,41030,50612,37388,49151,40472,44081,54221,38847,51156,33921,44680,48127,38710,48902,33436,44407,43373,39062,50116,34268,45652,30338,40610,47920,36278,48435,32356,42939,41366,37675,49334,33062,43626,29838,37507,48140,31771,42095,26739,35539,37571,29438,38388,24218,32092,21490,26087,33871,20799,27405,16238,21484,25225,16608,22120,12875,17174,10980,13179,17537,10097,13580,7732,10423,13393,7912,10700,6146,8242,6077,6224,8464,4728,6495,3578,4873,6457,3565,4909,2640,3644,3535,2742,3829,2090,2847,1587,2128,2914,1549,2116,1147,1600,1751,1134,1596,838,1190,645,836,1169,600,853,452,668,780,409,581,292,423,278,324,474,242,334,158,234,327,166,234,114,165,110,107,171,84,138,66,86,114,56,78,41,57,70,49,63,26,49,25,36,51,14,22,12,18,23,20,20,6,11,4,10,15,9,10,5,8,11,6,10,6,9,5,8,14,7,14,7,7,5,1,5,1,2,4,1,3,3,3,1,3,3,0,1,0,0,1,1,1,0,0,0,1,-1,
             -1
        };
    Memo1->Lines->Text=generate_svg(P);
    Memo1->Lines->SaveToFile("out.svg");
    }
//---------------------------------------------------------------------------

resulting SVG:

<svg xmlns="http://www.w3.org/2000/svg" viewBox="-100 -100 1100 1100">
 <g fill="none" stroke-width="1px">
  <rect stroke="black" x="0" y="0" height="1000" width="1000"/>
  <path stroke="aliceblue" transform="matrix(4.504505,0.000000,0.000000,-100.000000,0.000000,1000.000000)" d="M 0 0 L 0 3 L 1 3 L 2 4 L 3 3 L 4 4 L 5 5 L 6 3 L 7 3 L 8 1 L 9 2 L 10 2 L 11 0 L 12 0 L 13 0 L 14 0 L 15 0 L 16 0 L 17 0 L 18 0 L 19 0 L 20 0 L 21 0 L 22 0 L 23 0 L 24 0 L 25 0 L 26 0 L 27 0 L 28 0 L 29 0 L 30 0 L 31 0 L 32 0 L 33 0 L 34 0 L 35 0 L 36 1 L 37 1 L 38 2 L 39 2 L 40 2 L 41 1"/>
  <path stroke="antiquewhite" transform="matrix(4.504505,0.000000,0.000000,-24.705881,0.000000,1000.000000)" d="M 0 0 L 0 4 L 1 6 L 2 8 L 3 6 L 4 8 L 5 11 L 6 8 L 7 9 L 8 6 L 9 6 L 10 8 L 11 4 L 12 7 L 13 3 L 14 5 L 15 3 L 16 3 L 17 3 L 18 0 L 19 1 L 20 0 L 21 1 L 22 2 L 23 2 L 24 1 L 25 0 L 26 1 L 27 1 L 28 1 L 29 2 L 30 2 L 31 2 L 32 2 L 33 2 L 34 2 L 35 2 L 36 3 L 37 3 L 38 4 L 39 5 L 40 4 L 41 6 L 42 4 L 43 4 L 44 1 L 45 2 L 46 1 L 47 0 L 48 0 L 49 0 L 50 0 L 51 1"/>
  <path stroke="aqua" transform="matrix(4.504505,0.000000,0.000000,-6.158358,0.000000,1000.000000)" d="M 0 0 L 0 5 L 1 9 L 2 13 L 3 15 L 4 20 L 5 25 L 6 25 L 7 34 L 8 21 L 9 26 L 10 24 L 11 21 L 12 26 L 13 19 L 14 21 L 15 22 L 16 14 L 17 20 L 18 10 L 19 13 L 20 10 L 21 6 L 22 11 L 23 6 L 24 8 L 25 3 L 26 4 L 27 5 L 28 5 L 29 8 L 30 5 L 31 9 L 32 7 L 33 9 L 34 10 L 35 5 L 36 5 L 37 5 L 38 7 L 39 11 L 40 11 L 41 15 L 42 13 L 43 16 L 44 11 L 45 15 L 46 18 L 47 9 L 48 9 L 49 3 L 50 6 L 51 10 L 52 5 L 53 4 L 54 2 L 55 2 L 56 1 L 57 0 L 58 1 L 59 0 L 60 2 L 61 1 L 62 1 L 63 3 L 64 1 L 65 1"/>
  <path stroke="aquamarine" transform="matrix(4.504505,0.000000,0.000000,-1.538462,0.000000,1000.000000)" d="M 0 0 L 0 6 L 1 12 L 2 22 L 3 28 L 4 41 L 5 55 L 6 58 L 7 80 L 8 68 L 9 91 L 10 84 L 11 72 L 12 87 L 13 65 L 14 82 L 15 89 L 16 61 L 17 80 L 18 51 L 19 66 L 20 49 L 21 47 L 22 61 L 23 39 L 24 50 L 25 21 L 26 31 L 27 34 L 28 24 L 29 40 L 30 23 L 31 36 L 32 34 L 33 31 L 34 44 L 35 27 L 36 33 L 37 18 L 38 25 L 39 37 L 40 33 L 41 50 L 42 35 L 43 52 L 44 40 L 45 52 L 46 66 L 47 45 L 48 48 L 49 32 L 50 34 L 51 43 L 52 32 L 53 37 L 54 22 L 55 29 L 56 21 L 57 15 L 58 22 L 59 10 L 60 18 L 61 11 L 62 15 L 63 22 L 64 10 L 65 13 L 66 1 L 67 4 L 68 4 L 69 1 L 70 2 L 71 1 L 72 2 L 73 0 L 74 1 L 75 2 L 76 0 L 77 1 L 78 1 L 79 0 L 80 0 L 81 0 L 82 0 L 83 0 L 84 0 L 85 0 L 86 1"/>
  <path stroke="azure" transform="matrix(4.504505,0.000000,0.000000,-0.384545,0.000000,1000.000000)" d="M 0 0 L 0 7 L 1 17 L 2 33 L 3 47 L 4 77 L 5 108 L 6 126 L 7 179 L 8 167 L 9 226 L 10 245 L 11 235 L 12 308 L 13 224 L 14 303 L 15 300 L 16 263 L 17 318 L 18 216 L 19 278 L 20 204 L 21 238 L 22 282 L 23 180 L 24 229 L 25 138 L 26 185 L 27 211 L 28 145 L 29 194 L 30 122 L 31 168 L 32 137 L 33 136 L 34 168 L 35 113 L 36 150 L 37 93 L 38 123 L 39 132 L 40 118 L 41 165 L 42 124 L 43 174 L 44 156 L 45 167 L 46 215 L 47 150 L 48 204 L 49 134 L 50 167 L 51 208 L 52 127 L 53 180 L 54 107 L 55 145 L 56 119 L 57 97 L 58 131 L 59 81 L 60 100 L 61 63 L 62 78 L 63 99 L 64 61 L 65 83 L 66 43 L 67 56 L 68 58 L 69 35 L 70 46 L 71 19 L 72 26 L 73 13 L 74 14 L 75 18 L 76 7 L 77 8 L 78 4 L 79 8 L 80 9 L 81 3 L 82 6 L 83 2 L 84 6 L 85 4 L 86 6 L 87 11 L 88 5 L 89 6 L 90 2 L 91 3 L 92 6 L 93 2 L 94 4 L 95 4 L 96 2 L 97 1 L 98 2 L 99 2 L 100 1 L 101 2"/>
  <path stroke="beige" transform="matrix(4.504505,0.000000,0.000000,-0.096132,0.000000,1000.000000)" d="M 0 0 L 0 8 L 1 22 L 2 48 L 3 77 L 4 133 L 5 196 L 6 262 L 7 391 L 8 396 L 9 550 L 10 607 L 11 656 L 12 877 L 13 689 L 14 919 L 15 922 L 16 904 L 17 1104 L 18 823 L 19 1058 L 20 806 L 21 919 L 22 1120 L 23 792 L 24 1028 L 25 647 L 26 876 L 27 930 L 28 721 L 29 876 L 30 585 L 31 741 L 32 621 L 33 615 L 34 777 L 35 528 L 36 695 L 37 420 L 38 544 L 39 608 L 40 488 L 41 656 L 42 458 L 43 620 L 44 588 L 45 591 L 46 775 L 47 545 L 48 761 L 49 507 L 50 666 L 51 818 L 52 551 L 53 735 L 54 466 L 55 626 L 56 560 L 57 505 L 58 659 L 59 387 L 60 509 L 61 307 L 62 401 L 63 541 L 64 314 L 65 438 L 66 259 L 67 339 L 68 361 L 69 234 L 70 318 L 71 154 L 72 214 L 73 125 L 74 161 L 75 196 L 76 90 L 77 125 L 78 61 L 79 95 L 80 114 L 81 58 L 82 88 L 83 39 L 84 65 L 85 36 L 86 43 L 87 72 L 88 41 L 89 49 L 90 28 L 91 41 L 92 50 L 93 27 L 94 32 L 95 16 L 96 25 L 97 12 L 98 20 L 99 28 L 100 11 L 101 13 L 102 6 L 103 9 L 104 13 L 105 2 L 106 6 L 107 2 L 108 2 L 109 3 L 110 3 L 111 10 L 112 3 L 113 7 L 114 2 L 115 3 L 116 4 L 117 2 L 118 4 L 119 0 L 120 1 L 121 1 L 122 1 L 123 1 L 124 1 L 125 0 L 126 0 L 127 0 L 128 1"/>
  <path stroke="bisque" transform="matrix(4.504505,0.000000,0.000000,-0.024033,0.000000,1000.000000)" d="M 0 0 L 0 9 L 1 27 L 2 67 L 3 118 L 4 220 L 5 348 L 6 486 L 7 771 L 8 825 L 9 1214 L 10 1373 L 11 1633 L 12 2257 L 13 1906 L 14 2554 L 15 2557 L 16 2737 L 17 3353 L 18 2728 L 19 3572 L 20 2798 L 21 3278 L 22 3935 L 23 3040 L 24 3969 L 25 2675 L 26 3469 L 27 3713 L 28 2907 L 29 3630 L 30 2491 L 31 3269 L 32 2647 L 33 2733 L 34 3408 L 35 2315 L 36 3043 L 37 1931 L 38 2584 L 39 2710 L 40 2155 L 41 2789 L 42 1904 L 43 2566 L 44 2473 L 45 2331 L 46 3061 L 47 2134 L 48 2871 L 49 1939 L 50 2595 L 51 3186 L 52 2249 L 53 3031 L 54 1967 L 55 2575 L 56 2440 L 57 2253 L 58 2909 L 59 1827 L 60 2398 L 61 1549 L 62 1992 L 63 2595 L 64 1593 L 65 2098 L 66 1248 L 67 1661 L 68 1819 L 69 1347 L 70 1741 L 71 991 L 72 1320 L 73 792 L 74 964 L 75 1310 L 76 710 L 77 939 L 78 507 L 79 694 L 80 826 L 81 473 L 82 651 L 83 341 L 84 468 L 85 264 L 86 328 L 87 494 L 88 253 L 89 357 L 90 179 L 91 263 L 92 348 L 93 180 L 94 273 L 95 130 L 96 193 L 97 133 L 98 157 L 99 209 L 100 100 L 101 138 L 102 63 L 103 91 L 104 130 L 105 58 L 106 79 L 107 40 L 108 67 L 109 58 L 110 53 L 111 77 L 112 40 L 113 53 L 114 24 L 115 32 L 116 48 L 117 22 L 118 35 L 119 20 L 120 25 L 121 28 L 122 14 L 123 17 L 124 11 L 125 15 L 126 5 L 127 8 L 128 17 L 129 7 L 130 8 L 131 2 L 132 2 L 133 4 L 134 4 L 135 8 L 136 2 L 137 2 L 138 0 L 139 1 L 140 3 L 141 1 L 142 3 L 143 0 L 144 0 L 145 0 L 146 0 L 147 0 L 148 0 L 149 2 L 150 0 L 151 0 L 152 0 L 153 0 L 154 0 L 155 0 L 156 0 L 157 0 L 158 0 L 159 0 L 160 0 L 161 0 L 162 1 L 163 1"/>
  <path stroke="black" transform="matrix(4.504505,0.000000,0.000000,-0.006008,0.000000,1000.000000)" d="M 0 0 L 0 10 L 1 34 L 2 90 L 3 176 L 4 350 L 5 577 L 6 871 L 7 1436 L 8 1657 L 9 2534 L 10 2966 L 11 3764 L 12 5358 L 13 4882 L 14 6698 L 15 6791 L 16 7702 L 17 9604 L 18 8231 L 19 10947 L 20 8918 L 21 10913 L 22 12958 L 23 10509 L 24 13828 L 25 9786 L 26 12794 L 27 13566 L 28 11358 L 29 14039 L 30 9970 L 31 13110 L 32 10714 L 33 11362 L 34 14112 L 35 9696 L 36 12748 L 37 8299 L 38 10977 L 39 11669 L 40 9297 L 41 11941 L 42 8009 L 43 10755 L 44 10446 L 45 9502 L 46 12403 L 47 8392 L 48 11276 L 49 7651 L 50 10182 L 51 12325 L 52 9126 L 53 12174 L 54 8067 L 55 10627 L 56 10042 L 57 9292 L 58 12137 L 59 7975 L 60 10516 L 61 6945 L 62 8760 L 63 11373 L 64 7282 L 65 9587 L 66 5943 L 67 7862 L 68 8529 L 69 6461 L 70 8474 L 71 5139 L 72 6852 L 73 4337 L 74 5341 L 75 6935 L 76 4055 L 77 5350 L 78 3019 L 79 4024 L 80 4776 L 81 3023 L 82 4058 L 83 2251 L 84 3039 L 85 1851 L 86 2247 L 87 3039 L 88 1720 L 89 2289 L 90 1249 L 91 1742 L 92 2273 L 93 1290 L 94 1830 L 95 987 L 96 1372 L 97 972 L 98 978 L 99 1372 L 100 767 L 101 1038 L 102 538 L 103 722 L 104 994 L 105 529 L 106 710 L 107 367 L 108 535 L 109 509 L 110 393 L 111 589 L 112 316 L 113 401 L 114 226 L 115 297 L 116 389 L 117 197 L 118 290 L 119 143 L 120 202 L 121 226 L 122 147 L 123 211 L 124 103 L 125 140 L 126 79 L 127 101 L 128 142 L 129 67 L 130 106 L 131 51 L 132 67 L 133 75 L 134 46 L 135 65 L 136 32 L 137 45 L 138 36 L 139 42 L 140 55 L 141 24 L 142 34 L 143 11 L 144 12 L 145 25 L 146 9 L 147 21 L 148 8 L 149 17 L 150 10 L 151 9 L 152 11 L 153 5 L 154 14 L 155 5 L 156 7 L 157 6 L 158 3 L 159 7 L 160 4 L 161 5 L 162 7 L 163 6 L 164 6 L 165 3 L 166 2 L 167 0 L 168 1 L 169 2 L 170 0 L 171 2 L 172 2 L 173 3 L 174 2 L 175 2 L 176 0 L 177 0 L 178 0 L 179 0 L 180 1 L 181 1 L 182 0 L 183 0 L 184 0 L 185 1 L 186 2 L 187 1 L 188 2 L 189 0 L 190 0 L 191 0 L 192 0 L 193 1 L 194 1 L 195 2"/>
  <path stroke="blanchedalmond" transform="matrix(4.504505,0.000000,0.000000,-0.001502,0.000000,1000.000000)" d="M 0 0 L 0 11 L 1 41 L 2 118 L 3 251 L 4 532 L 5 924 L 6 1500 L 7 2580 L 8 3164 L 9 5018 L 10 6108 L 11 8193 L 12 12030 L 13 11599 L 14 16410 L 15 16947 L 16 20329 L 17 25638 L 18 23361 L 19 31525 L 20 26494 L 21 33543 L 22 39633 L 23 33833 L 24 44866 L 25 33020 L 26 43543 L 27 45974 L 28 41030 L 29 50612 L 30 37388 L 31 49151 L 32 40472 L 33 44081 L 34 54221 L 35 38847 L 36 51156 L 37 33921 L 38 44680 L 39 48127 L 40 38710 L 41 48902 L 42 33436 L 43 44407 L 44 43373 L 45 39062 L 46 50116 L 47 34268 L 48 45652 L 49 30338 L 50 40610 L 51 47920 L 52 36278 L 53 48435 L 54 32356 L 55 42939 L 56 41366 L 57 37675 L 58 49334 L 59 33062 L 60 43626 L 61 29838 L 62 37507 L 63 48140 L 64 31771 L 65 42095 L 66 26739 L 67 35539 L 68 37571 L 69 29438 L 70 38388 L 71 24218 L 72 32092 L 73 21490 L 74 26087 L 75 33871 L 76 20799 L 77 27405 L 78 16238 L 79 21484 L 80 25225 L 81 16608 L 82 22120 L 83 12875 L 84 17174 L 85 10980 L 86 13179 L 87 17537 L 88 10097 L 89 13580 L 90 7732 L 91 10423 L 92 13393 L 93 7912 L 94 10700 L 95 6146 L 96 8242 L 97 6077 L 98 6224 L 99 8464 L 100 4728 L 101 6495 L 102 3578 L 103 4873 L 104 6457 L 105 3565 L 106 4909 L 107 2640 L 108 3644 L 109 3535 L 110 2742 L 111 3829 L 112 2090 L 113 2847 L 114 1587 L 115 2128 L 116 2914 L 117 1549 L 118 2116 L 119 1147 L 120 1600 L 121 1751 L 122 1134 L 123 1596 L 124 838 L 125 1190 L 126 645 L 127 836 L 128 1169 L 129 600 L 130 853 L 131 452 L 132 668 L 133 780 L 134 409 L 135 581 L 136 292 L 137 423 L 138 278 L 139 324 L 140 474 L 141 242 L 142 334 L 143 158 L 144 234 L 145 327 L 146 166 L 147 234 L 148 114 L 149 165 L 150 110 L 151 107 L 152 171 L 153 84 L 154 138 L 155 66 L 156 86 L 157 114 L 158 56 L 159 78 L 160 41 L 161 57 L 162 70 L 163 49 L 164 63 L 165 26 L 166 49 L 167 25 L 168 36 L 169 51 L 170 14 L 171 22 L 172 12 L 173 18 L 174 23 L 175 20 L 176 20 L 177 6 L 178 11 L 179 4 L 180 10 L 181 15 L 182 9 L 183 10 L 184 5 L 185 8 L 186 11 L 187 6 L 188 10 L 189 6 L 190 9 L 191 5 L 192 8 L 193 14 L 194 7 L 195 14 L 196 7 L 197 7 L 198 5 L 199 1 L 200 5 L 201 1 L 202 2 L 203 4 L 204 1 L 205 3 L 206 3 L 207 3 L 208 1 L 209 3 L 210 3 L 211 0 L 212 1 L 213 0 L 214 0 L 215 1 L 216 1 L 217 1 L 218 0 L 219 0 L 220 0 L 221 1"/>
 </g>
</svg>

And screenshot:

As you can see I just replaced the /n with nothing, and added n as first number in te sequence for each graph. I also added full list of named colors in SVG , you can play with the order so the darker colors goes first now they ordered alphabetically which is not ideal as you can see many graphs are very close to white making them almost invisible.

Now if you do not want to code you can do this manually too. Just convert your data in notepad by replacing /n with nothing and than add the L (for example by replacing the ,) and add incrementing x coordinate (sadly this one you need to do manually unless you got some macro in text editor). And of coarse add the header and SVG stuff.

From this you just open the SVG in browser and take screenshot. Then in paint you can add what ever you want. If you study the SVG you can even do all the stuff in the SVG directly (too lazy for that) like adding grid, labels, scales legend etc ...

The viewbox gives you scaling/resolution of your graph with some border. The transforms is computed like this:

transform="matrix(1000.0/max(x),0.0,0.0,-1000.0*scale/divider,0.0,1000.0)"

Where x is the max x of all graphs, divider is the n from /n of al lthe values for actual processed graph and scale is the y scale (as distributions probabilities tend to be much less than 1.0 value). Assuming graph starts at (0,0) and 1000.0 is the resolution from viewbox without border. This will ensure that your data do not need to be converted and graph matches standard math notation.

So here is empty SVG:

<svg xmlns="http://www.w3.org/2000/svg" viewBox="-100 -100 1100 1100">
 <g fill="none" stroke-width="1px">
  <rect stroke="black" x="0" y="0" height="1000" width="1000"/>
  <path stroke="***HERE GOES COLOR NAME***" transform="matrix(***HERE COMPUTED TRANSFORM MATRIX***)" d="M 0 0 **HERE GRAPH: L x0 y0 L x1 y1 ... ** "/>
 </g>
</svg>

so for each graph add the line <path ...> compute the transform matrix values and add the graph data after d="M 0 0 in form of L 0 P(0) L 1 P(1) ....

You can add/tweak whatever you want it is just text file... However I am no expert in SVG (I just coded decoder/encoder for my vector CAD/CAM SW I needed some years ago for work and using it since but there my knowledge ends) so there might be even simpler ways to do this with SVG (like get rid of the incremental x coordinate). If you could obtain your data in relative manner then you could for example use l 1 dP[x] instead of L x P[x] which would be doable by simple replace in notepad ...

Answer 2

I have encounter the same problem to draw curve properly without using Microsoft Excel charts and I have used charjs that you can find in https://www.chartjs.org

This tool works very well for my job.

All my curve's data (X/Y coordinate) are put in javascript files that I include at begin of html file. But in your situation, you can simply copy (using Paste/Copy) your variables directly in JavaScript part of html file !

You can even find some javascript code to extract the HTML image in PNG file that you can put in other editor program.

I have seen that you have a computer and it is an android.

So if you will make graphics on internet, I propose you to see the 2 following links

https://webdesign.tutsplus.com/tutorials/how-to-create-a-simple-line-chart-with-chartjs--cms-28129

https://codepen.io/tutsplus/pen/JRVgRB

CodePen site is a web site that allows you to define graphics on the Web knowing HTML, JavaScript and CSS.

But in your case, I think that the better thing is to find some example on Google in searching "CodePen" "chartjs". I have tested and I find a lot of example of CodePen for Chartjs.

This link display a lof of examples of chartjs graphs. https://codepen.X/tag/chartjs

make a Paste/Copy of link and replace X by "io" to work around StackOverflow limitation that request some code

I know that you have no experiment in coding but you can perhaps try to modify code using already written code using CodePen user interface.