Are there any good (if possible scientific) resources available (web or books) about overlap processing. I am not that interested in the effects of using overlap processing and windows when analyzing a signal, since the requirements are different. It is more about the following Real Time situation: (I am currently dealing with audio signals)
- Dividing a signal into smaller parts.
- Creating overlap windows.
- FFTing the windowed chunks.
- Do processing in the frequency domain.
- IFFT the results.
- put the chunks together to a continuous stream.
I am especially interested in the influence of the window used on the resulting error as well as the effect of the overlap length. However I couldn't find any good resources that deal with the subject in detail. Any suggestions?
Edit:
After some discussions if using a window function is appropriate, I found a decent handout explaining the overlap and add/save method. http://www.ece.tamu.edu/~deepa/ecen448/handouts/08c/10_Overlap_Save_Add_handouts.pdf
However, after doing some tests, I noticed that the windowed version would perform more accurate in most cases than the overlap & add/save method. Could anybody confirm this? I don't want to jump to any conclusions regarding computation time though....
Edit2:
Here are some graphs from my tests:
I created a signal, which consists of three cosine waves
I used this filter function in the time domain for filtering. (It's symmetric, as it is applied to the whole output of the FFT, which also is symmetric for real input signals)

The output of the IFFT looks like this: It can be seen that low frequencies are attenuated more than frequency in the mid range.
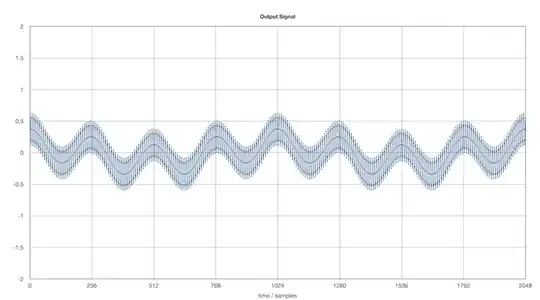
For the overlap add/save and the windowed processing I divided the input signal into 8 chunks of 256 samples. After reassembling them they look like that. (sample 490 - 540)

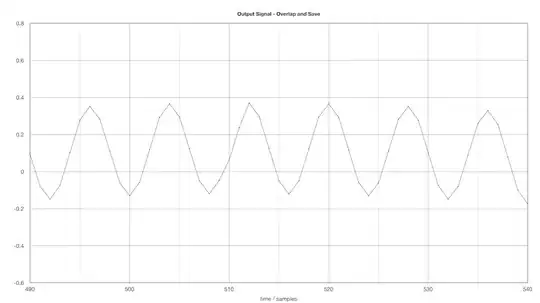
It can be seen that the overlap add/save processes differ from the windowed version at the point where chunks are put together (sample 511). This is the error which leads to different results when comparing windowed process and overlap add/save. The windowed process is closer to the one processed in one big junk.
However, I have no idea why they are there or if they shouldn't be there at all.