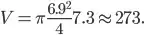smallest enclosing cylinder

Question

Is there an algorithm for finding of an enclosing cylinder with the smallest radius for a 3D cloud of dots? I know that 2D case with the smallest enclosing circle is solved (for example this thread Smallest enclosing circle in Python, error in the code), but is there any working approach for 3D?

---

EDIT1: OBB. Below is an example of an arc-shaped cloud of dots. The smallest enclosing circle was found by this tool https://www.nayuki.io/page/smallest-enclosing-circle

Circle is defined by three dots of which two are lying almost on a diameter, so it is easy to estimate where the central axis is. "Boxing" of dots will yield a center of the box obviously much shifted from the true center.

I conclude, that OBB approach is not general.

---

EDIT2: PCA. Below is an example of PCA analysis of a tight dot cloud vs. dot cloud with outliers. For the tight dot cloud PCA predicts the cylinder direction satisfactorily. But if there is a small number of outliers, compared to the main cloud, than PCA will basically ignore them, yielding vectors which are very far from the true axis of an enclosing cylinder. In the example below the true geometrical axis of an enclosing cylinder is shown in black.

I conclude that PCA approach is not general.

---

EDIT3: OBB vs. PCA and OLS. A major difference - OBB relies only on a geometrical shape, while PCA and OLS are dependent from the overall number of points, including those in the middle of the set, which do not affect the shape. In order to make them more efficient, a data preparation step can be included. First, find the convex hull. Second, exclude all internal points. Then, points along the hull can be distributed unevenly. I'd suggest to remove all of them, leaving only the polygonal hull body, and cover it with mesh, where nodes will be new points. Application of PCA or OLS to this new cloud of points should provide much more accurate estimation of the cylinder axis.

All this can be unnecessary, if OBB provides an axis, as much parallel to the enclosing cylinder axis, as possible.

---

EDIT4: published approaches. @meowgoesthedog: paper by Michel Petitjean ("About the Algebraic Solutions of Smallest Enclosing Cylinders Problems") could help, but I'm insufficiently qualified to convert it to a working program. Author himself did it (module CYL here http://petitjeanmichel.free.fr/itoweb.petitjean.freeware.html). But at the conclusions in the paper he says: "and the present software, named CYL, downloadable for free at http://petitjeanmichel.free.fr/itoweb.petitjean.freeware.html, is neither claimed to offer the best possible implementations of the methods nor is claimed to work better than other cylinder computation softwares." Other phrases from the paper also makes an impression, that it is an experimental approach, which was not thoroughly validated. I'll try to use it, anyway.

@Ripi2: this paper by Timothy M. Chan is also a bit too complicated for me. I'm not an expert of that level in mathematics, to be able to convert to a tool.

@Helium_1s2: probably, it is a good suggestion, however, it is much less detailed compared to two papers above. Also, not validated.

---

EDIT5: reply for user1717828. Two most distant points vs. cylinder axis. A counter example - 8 points in a shape of cube, fit in a cylinder. The biggest distance between two points - green diagonal. Obviously not parallel to cylinder axis.

"Middle-points" approach by Ripi2: it works only in 2D. In a 3D case the cylinder axis may not intersect a single segment between any two points.

Answer 1

1. compute OBB

   so either use PCA or this

   • How to Compute OBB of Multiple Curves?

   to obtain 3D OBB. The code in the link must be ported to 3D but the principle is the same. Here my more advanced 3D OBB approximation using recursive search on cube_map (the code and approach in here is inferior to it).

2. initial guess

   so OBB will give you oriented bounding box. Its biggest side will be parallel to rotation axis of your cylinder. So lets start with cylinder outscribing this OBB. So the central axis will be center of the OBB and parallel to its biggest side. (if you do not have biggest side then you need to check all 3 combinations). The diameter will be the bigger of the remaining sides.

3. fit cylinder

   Now just try "all" combinations of offset and radius (may be also height) enclosing all your points near initial guess and remember the best one (according to your wanted specs). You can use any optimization method for this but my favorite is this:

   • How approximation search works

The validity of the result depends on the fitting process. But do not get too wild with the nested fitting as the complexity goes wild too.

[Edit1] 3D OBB in C++

I was curious and got some time today so I encoded 3D OBB similar to the 2D example linked above. Looks like its working. This is preview:

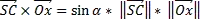
I used 2 clusters to verify the orientation... Here the code (in form of simple C++ class):

//---------------------------------------------------------------------------
class OBB3D
    {
public:
    double p0[3],u[3],v[3],w[3];    // origin,3 axises sorted by size asc
    double V,l[3];                  // volume, and { |u|,|v|,|w| }
    double p[8*3];                  // corners

    OBB3D()     {}
    OBB3D(OBB3D& a) { *this=a; }
    ~OBB3D()    {}
    OBB3D* operator = (const OBB3D *a) { *this=*a; return this; }
    //OBB3D* operator = (const OBB3D &a) { ...copy... return this; }

    void compute(double *pnt,int num)       // pnt[num] holds num/3 points
        {
        OBB3D o;                            // temp OBB values
        int i,j;
        double a,_a,a0,a1,da,ca,sa; int ea; // search angles
        double b,_b,b0,b1,db,cb,sb; int eb;
        double c,_c,c0,c1,dc,cc,sc; int ec;
        double u0[3],v0[3],pmin[3],pmax[3],q,*qq;
        const double deg=M_PI/180.0;
        p0[0]=0.0; u[0]=1.0; v[0]=0.0; w[0]=0.0; l[0]=0.0; V=-1.0;
        p0[1]=0.0; u[1]=0.0; v[1]=1.0; w[1]=0.0; l[1]=0.0;
        p0[2]=0.0; u[2]=0.0; v[2]=0.0; w[2]=1.0; l[2]=0.0;
        if (num<3) { V=0.0; return; }

        a0=0; a1=360.0*deg; da=10.0*deg; _a=a0;
        b0=0; b1= 90.0*deg; db=10.0*deg; _b=b0;
        c0=0; c1= 90.0*deg; dc=10.0*deg; _c=c0;
        // recursively increase precision
        for (j=0;j<5;j++)
            {
            // try all 3D directions with some step da,db
            for (ea=1,a=a0;ea;a+=da){ if (a>=a1) { a=a1; ea=0; } ca=cos(a); sa=sin(a);
             for (eb=1,b=b0;eb;b+=db){ if (b>=b1) { b=b1; eb=0; } cb=cos(b); sb=sin(b);
                // spherical to cartesian direction
                o.w[0]=cb*ca;
                o.w[1]=cb*sa;
                o.w[2]=sb;
                // init u,v from cross product
                vector_ld(u0,1.0,0.0,0.0);
                if (fabs(vector_mul(u0,o.w))>0.75)  // |dot(u,w)>0.75| measn near (anti)parallel
                 vector_ld(u0,0.0,1.0,0.0);
                vector_mul(v0,o.w,u0);  // v0 = cross(w,u0)
                vector_mul(u0,v0,o.w);  // u0 = cross(v0,w)
                vector_one(u0,u0);      // u0/=|u0|
                vector_one(v0,v0);      // v0/=|v0|
                // try all rotations within u0,v0 plane
                for (ec=1,c=c0;ec;c+=dc){ if (c>=c1) { c=c1; ec=0; } cc=cos(c); sc=sin(c);
                    for (i=0;i<3;i++)
                        {
                        o.u[i]=(u0[i]*cc)-(v0[i]*sc);
                        o.v[i]=(u0[i]*sc)+(v0[i]*cc);
                        }
                    // now u,v,w holds potential obb axises socompute min,max
                    pmin[0]=pmax[0]=vector_mul(pnt,o.u);    // dot(pnt,u);
                    pmin[1]=pmax[1]=vector_mul(pnt,o.v);    // dot(pnt,v);
                    pmin[2]=pmax[2]=vector_mul(pnt,o.w);    // dot(pnt,w);
                    for (i=0;i<num;i+=3)
                        {
                        q=vector_mul(pnt+i,o.u); if (pmin[0]>q) pmin[0]=q; if (pmax[0]<q) pmax[0]=q;
                        q=vector_mul(pnt+i,o.v); if (pmin[1]>q) pmin[1]=q; if (pmax[1]<q) pmax[1]=q;
                        q=vector_mul(pnt+i,o.w); if (pmin[2]>q) pmin[2]=q; if (pmax[2]<q) pmax[2]=q;
                        }
                    // compute V,l from min,max
                    for (o.V=1.0,i=0;i<3;i++) { o.l[i]=pmax[i]-pmin[i]; o.V*=o.l[i]; }
                    // remember best solution u,v,w,V,l and compute p0
                    if ((V<0.0)||(V>o.V))
                        {
                        *this=o; _a=a; _b=b; _c=c;
                        for (i=0;i<3;i++) p0[i]=(pmin[0]*u[i])+(pmin[1]*v[i])+(pmin[2]*w[i]);
                        }
                    }
                }}
            a0=(_a-0.5*da); a1=a0+da; da*=0.1;
            b0=(_b-0.5*db); b1=b0+db; db*=0.1;
            c0=(_c-0.5*dc); c1=c0+dc; dc*=0.1;
            }
        // sort axises
                      { i=0; qq=u; }    // w is max
        if (l[1]>l[i]){ i=1; qq=v; }
        if (l[2]>l[i]){ i=2; qq=w; }
        for (j=0;j<3;j++) { q=w[j]; w[j]=qq[j]; qq[j]=q; } q=l[2]; l[2]=l[i]; l[i]=q;
                      { i=0; qq=u; }    // v is 2nd max
        if (l[1]>l[i]){ i=1; qq=v; }
        for (j=0;j<3;j++) { q=v[j]; v[j]=qq[j]; qq[j]=q; } q=l[1]; l[1]=l[i]; l[i]=q;
        // compute corners from p0,u,v,w,l
        for (i=0;i<3;i++)
            {
            j=i;
            p[j]=p0[i]                                    ; j+=3;
            p[j]=p0[i]+(l[0]*u[i])                        ; j+=3;
            p[j]=p0[i]+(l[0]*u[i])+(l[1]*v[i])            ; j+=3;
            p[j]=p0[i]            +(l[1]*v[i])            ; j+=3;
            p[j]=p0[i]                        +(l[2]*w[i]); j+=3;
            p[j]=p0[i]+(l[0]*u[i])            +(l[2]*w[i]); j+=3;
            p[j]=p0[i]+(l[0]*u[i])+(l[1]*v[i])+(l[2]*w[i]); j+=3;
            p[j]=p0[i]            +(l[1]*v[i])+(l[2]*w[i]); j+=3;
            }
        }
    void gl_draw()
        {
        glBegin(GL_LINES);
        glVertex3dv(p+ 0); glVertex3dv(p+ 3);
        glVertex3dv(p+ 3); glVertex3dv(p+ 6);
        glVertex3dv(p+ 6); glVertex3dv(p+ 9);
        glVertex3dv(p+ 9); glVertex3dv(p+ 0);
        glVertex3dv(p+12); glVertex3dv(p+15);
        glVertex3dv(p+15); glVertex3dv(p+18);
        glVertex3dv(p+18); glVertex3dv(p+21);
        glVertex3dv(p+21); glVertex3dv(p+12);
        glVertex3dv(p+ 0); glVertex3dv(p+12);
        glVertex3dv(p+ 3); glVertex3dv(p+15);
        glVertex3dv(p+ 6); glVertex3dv(p+18);
        glVertex3dv(p+ 9); glVertex3dv(p+21);
        glEnd();
        }
    } obb;
//---------------------------------------------------------------------------

You just call compute with point cloud data where num is 3x number of points. The result is stored as unit basis vectors u,v,w and origin p0 along with sizes l[] per each axis or as 8 corner points of OBB p

The stuff works simply by trying "all" spherical positions with some step for the w axis and then try all u,v polar positions perpendicular to each and w remembering the minimal volume OBB. Then recursively search only positions near found best solution with smaller step to improve accuracy.

I think this should provide fine start point. If you implement the minimal circle instead of u,v rotation (loop for (ec=1,c=c0;ec;c+=dc)) then you might obtain your cylinder directly from this search.

The code is not optimized yet (some parts like w axis check) can be moved to lower layer of nested for loop. But I wanted to keep this simple and understandable as much as I could instead.

[Edit2] 3D OBC in C++

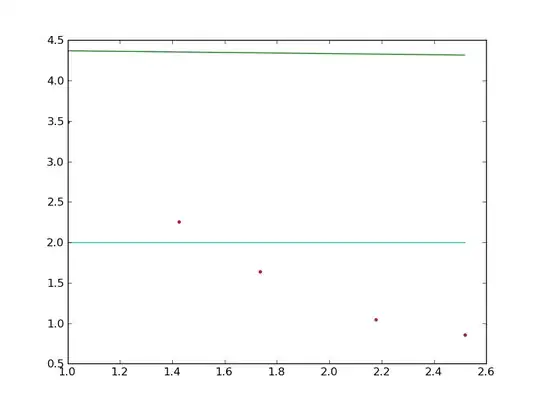
I managed to modify my 3D OBB by replacing U,V search with minimal enclosing circle (hope I implemented it right but it looks like it...) that find the minimal enclosing 2D circle of all the points projected on UV plane which makes it an Oriented Bounding Cylinder parallel to W. I used the first approach from pdf from your link (using bisector). Here the result:

In blue is the 3D OBB and in brown/orange-ish is the found 3D OBC. Here the code:

class OBC3D                         // 3D Oriented Bounding Cylinder
    {
public:
    double p0[3],u[3],v[3],w[3];    // basecenter,3 axises
    double V,r,h;                   // volume, radius height
    double p1[3];                   // other base center

    OBC3D()     {}
    OBC3D(OBC3D& a) { *this=a; }
    ~OBC3D()    {}
    OBC3D* operator = (const OBC3D *a) { *this=*a; return this; }
    //OBC3D* operator = (const OBC3D &a) { ...copy... return this; }

    void compute(double *pnt,int num)       // pnt[num] holds num/3 points
        {
        OBC3D o;                            // temp OBB values
        int i,j,k,kk,n;
        double a,_a,a0,a1,da,ca,sa; int ea; // search angles
        double b,_b,b0,b1,db,cb,sb; int eb;
        double pmin[3],pmax[3],q,qq,*pnt2,p[3],c0,c1,u0,v0,du,dv,dr;
        const double deg=M_PI/180.0;
        p0[0]=0.0; u[0]=1.0; v[0]=0.0; w[0]=0.0; V=-1.0;
        p0[1]=0.0; u[1]=0.0; v[1]=1.0; w[1]=0.0; r=0.0;
        p0[2]=0.0; u[2]=0.0; v[2]=0.0; w[2]=1.0; h=0.0;
        if (num<3) { V=0.0; return; }
        // prepare buffer for projected points
        pnt2=new double[num];

        a0=0; a1=360.0*deg; da=10.0*deg; _a=a0;
        b0=0; b1= 90.0*deg; db=10.0*deg; _b=b0;
        // recursively increase precision
        for (k=0;k<5;k++)
            {
            // try all 3D directions with some step da,db
            for (ea=1,a=a0;ea;a+=da){ if (a>=a1) { a=a1; ea=0; } ca=cos(a); sa=sin(a);
             for (eb=1,b=b0;eb;b+=db){ if (b>=b1) { b=b1; eb=0; } cb=cos(b); sb=sin(b);
                // spherical to cartesian direction
                o.w[0]=cb*ca;
                o.w[1]=cb*sa;
                o.w[2]=sb;
                // init u,v from cross product
                vector_ld(o.u,1.0,0.0,0.0);
                if (fabs(vector_mul(o.u,o.w))>0.75) // |dot(u,w)>0.75| measn near (anti)parallel
                 vector_ld(o.u,0.0,1.0,0.0);
                vector_mul(o.v,o.w,o.u);    // v0 = cross(w,u0)
                vector_mul(o.u,o.v,o.w);    // u0 = cross(v0,w)
                vector_one(o.u,o.u);        // u0/=|u0|
                vector_one(o.v,o.v);        // v0/=|v0|
                // now u,v,w holds potential obb axises so compute min,max and convert to local coordinates
                pmin[0]=pmax[0]=vector_mul(pnt,o.u);    // dot(pnt,u);
                pmin[1]=pmax[1]=vector_mul(pnt,o.v);    // dot(pnt,v);
                pmin[2]=pmax[2]=vector_mul(pnt,o.w);    // dot(pnt,w);
                for (i=0;i<num;i+=3)
                    {
                    q=vector_mul(pnt+i,o.u); if (pmin[0]>q) pmin[0]=q; if (pmax[0]<q) pmax[0]=q; pnt2[i+0]=q;
                    q=vector_mul(pnt+i,o.v); if (pmin[1]>q) pmin[1]=q; if (pmax[1]<q) pmax[1]=q; pnt2[i+1]=q;
                    q=vector_mul(pnt+i,o.w); if (pmin[2]>q) pmin[2]=q; if (pmax[2]<q) pmax[2]=q; pnt2[i+2]=q;
                    }
                // [compute min enclosing circle]
                n=0;
                // center (u0,v0) = avg( pnt2 )
                for (u0=0.0,v0=0.0,i=0;i<num;i+=3)
                    {
                    u0+=pnt2[i+0];
                    v0+=pnt2[i+1];
                    } q=3.0/double(num); u0*=q; v0*=q;
                // r = max(|pnt2 - (u0,v0)|)
                for (o.r=0.0,i=0;i<num;i+=3)
                    {
                    c0=pnt2[i+0]-u0;
                    c1=pnt2[i+1]-v0;
                    q=(c0*c0)+(c1*c1);
                    if (o.r<q) o.r=q;
                    } o.r=sqrt(o.r);
                for (kk=0;kk<4;kk++)
                    {
                    // update edgepoints count n
                    qq=o.r*o.r;
                    for (i=n;i<num;i+=3)
                        {
                        c0=pnt2[i+0]-u0;
                        c1=pnt2[i+1]-v0;
                        q=fabs((c0*c0)+(c1*c1)-qq);
                        if (q<1e-10)
                            {
                            pnt2[n+0]=pnt2[i+0];
                            pnt2[n+1]=pnt2[i+1];
                            pnt2[n+2]=pnt2[i+2]; n+=3;
                            }
                        }
                    // compute bisector (du,dv)
                    for (du=0.0,dv=0.0,i=0;i<n;i+=3)
                        {
                        du+=pnt2[i+0]-u0;
                        dv+=pnt2[i+1]-v0;
                        } q=1.0/sqrt((du*du)+(dv*dv)); du*=q; dv*=q;
                    // try to move center towards edge points as much as possible
                    for (dr=0.1*o.r,j=0;j<5;)
                        {
                        u0+=dr*du;
                        v0+=dr*dv;
                        // q = max(|pnt2 - (u0,v0)|)
                        for (qq=0.0,i=0;i<num;i+=3)
                            {
                            c0=pnt2[i+0]-u0;
                            c1=pnt2[i+1]-v0;
                            q=(c0*c0)+(c1*c1);
                            if (qq<q) qq=q;
                            } qq=sqrt(qq);
                        // recursively increase precision
                        if (qq>o.r)
                            {
                            u0-=dr*du;
                            v0-=dr*dv;
                            dr*=0.1;
                            j++;
                            }
                        else o.r=qq;
                        }
                    }

                // compute h,V
                o.h=pmax[2]-pmin[2];
                o.V=M_PI*o.r*o.r*o.h;
                // remember best solution u,v,w,V,l and compute p0
                if ((V<0.0)||(V>o.V))
                    {
                    *this=o; _a=a; _b=b;
                    for (i=0;i<3;i++) p0[i]=(u0*u[i])+(v0*v[i])+(pmin[2]*w[i]);
                    }
                }}
            a0=(_a-0.5*da); a1=a0+da; da*=0.1;
            b0=(_b-0.5*db); b1=b0+db; db*=0.1;
            }
        // compute corners from p0,u,v,w,l
        for (i=0;i<3;i++) p1[i]=p0[i]+(h*w[i]);
        delete[] pnt2;
        }
    void gl_draw()
        {
        int i,j,n=36;
        double a,da=2.0*M_PI/double(n),p[3],uu,vv;
        glBegin(GL_LINES);
        glVertex3dv(p0); glVertex3dv(p1);
        glEnd();
        glBegin(GL_LINE_LOOP);
        for (a=0.0,i=0;i<n;i++,a+=da)
            {
            uu=r*cos(a);
            vv=r*sin(a);
            for (j=0;j<3;j++) p[j]=p0[j]+(u[j]*uu)+(v[j]*vv);
            glVertex3dv(p);
            }
        glEnd();
        glBegin(GL_LINE_LOOP);
        for (a=0.0,i=0;i<n;i++,a+=da)
            {
            uu=r*cos(a);
            vv=r*sin(a);
            for (j=0;j<3;j++) p[j]=p1[j]+(u[j]*uu)+(v[j]*vv);
            glVertex3dv(p);
            }
        glEnd();
        }
    };
//---------------------------------------------------------------------------

Usage is the same ... I tested with this:

OBB3D obb;
OBC3D obc;
void compute()
    {
    int i,n=500;
    // random pnt cloud
    Randomize();
    RandSeed=98123456789;
    pnt.allocate(3*n); pnt.num=0;

    // random U,V,W basis vectors
    double u[3],v[3],w[3],x,y,z,a;
    for (i=0;i<3;i++) w[i]=Random()-0.5;    // random direction
    vector_one(w,w);        // w/=|w|
    vector_ld(u,1.0,0.0,0.0);
    if (fabs(vector_mul(u,w))>0.75) // |dot(u,w)>0.75| measn near (anti)parallel
     vector_ld(u,0.0,1.0,0.0);
    vector_mul(v,w,u);      // v = cross(w,u)
    vector_mul(u,v,w);      // u = cross(v,w)
    vector_one(u,u);        // u/=|u|
    vector_one(v,v);        // v/=|v|
    // random cylinder point cloud
    for (i=0;i<n;i++)
        {
        a=2.0*M_PI*Random();
        x= 0.5+(0.75*(Random()-0.5))*cos(a);
        y=-0.3+(0.50*(Random()-0.5))*sin(a);
        z= 0.4+(0.90*(Random()-0.5));
        pnt.add((x*u[0])+(y*v[0])+(z*w[0]));
        pnt.add((x*u[1])+(y*v[1])+(z*w[1]));
        pnt.add((x*u[2])+(y*v[2])+(z*w[2]));
        }
    obb.compute(pnt.dat,pnt.num);
    obc.compute(pnt.dat,pnt.num);
    }

Where List<double> pnt is my dynamic array template double pnt[]. Which is not important in here.

Beware that if you chose too big initial step (da,db) for the W direction search you might miss the correct solution by trapping itself inside local minimum.

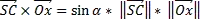
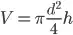Answer 2

Conceptual Answer

1. Find the two points with the greatest distance h between them. They are on the faces of the cylinder and the line connecting them will be parallel to the axis of the cylinder.

2. Project all points on the plane perpendicular to that axis.

3. Find the two points with the greatest distance d between them on that plane. They define the circle whose diameter d is that of the cylinder.

4. The cylinder with the smallest possible volume* containing all points has

.

* This assumes there is only one pair of points with the greatest distance between them defining the axis of the cylinder. If there's a chance two pairs of points share the greatest value, repeat steps 2-4 for each pair and choose the cylinder with the smallest diameter.

Python Answer

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib notebook

from numpy.linalg import norm
from scipy.spatial.distance import pdist, squareform

Generate points if you don't have them already:

np.random.seed(0)
N = 30
M = np.random.randint(-3,3,(N,3))
print(M)

[[ 1  2 -3]
 [ 0  0  0]
 [-2  0  2]
 [-1  1 -3]
 [-3  1 -1]
 ...
 [ 1 -3  1]
 [ 0 -1  2]]

Calculate the distance between every possible pair of points and select the pair with the greatest distance.

max_dist_pair = list(pd.DataFrame(squareform(pdist(M))).stack().idxmax())
p1 = M[max_dist_pair[0]]
p2 = M[max_dist_pair[1]]
print(f"Points defining cylinder faces: {p1}, {p2}")
print(f"Length of cylinder: {norm(p1-p2)}")

Points defining cylinder faces: [-1 -3 -3], [1 2 2]
Length of cylinder: 7.3484692283495345

Graph the points showing all the points in blue, with the maximally separated points in red.

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(*M.T, c = ['red' if i in max_dist_pair else 'blue' for i in range(N)])

ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")

plt.show()

Here is the same plot rotated so we're looking along the axis between the two red dots.

The above view is the same thing as the points being projected on the plane perpendicular to the axis of the cylinder. Find the smallest circle that contains points in this plane. We do this by finding the displacement of each point to the axis, then finding the largest distance between two points.

perp_disp = (np.cross(p2-p1, M-p1))/norm(p2-p1) # Get perpendicular displacement vectors.
print(perp_disp)

[[-3.40206909  1.36082763  0.        ]
 [ 0.         -0.13608276  0.13608276]
 [ 1.36082763 -2.04124145  1.4969104 ]
 [-2.72165527  0.          1.08866211]
 [-1.36082763 -1.90515869  2.44948974]
 [ 0.68041382 -0.95257934  0.68041382]
 [ 2.72165527  0.68041382 -1.76907593]
 ...
 [ 0.          0.27216553 -0.27216553]
 [ 0.         -0.40824829  0.40824829]
 [ 2.72165527  0.27216553 -1.36082763]
 [ 2.04124145 -0.68041382 -0.13608276]]

The largest distance is found by doing the same pdist used trick above.

max_perp_disp_pair = list(pd.DataFrame(squareform(pdist(perp_disp))).stack().idxmax())
perp_p1 = M[max_perp_disp_pair[0]]
perp_p2 = M[max_perp_disp_pair[1]]
print(perp_p1, perp_p2)

[ 1  2 -3] [-3 -2  1]

Finally, we get the diameter of the cylinder.

print(norm(perp_p1 - perp_p2))
6.92820323028

The smallest volume of a cylinder that can contain these points is

Notes

• The maximum distance between points was found usings Numpy's pairwise distance function pdist. Then it was formatted with squareform to throw it into a Pandas DataFrame so the indices of both points could be easily found using idxmax. There is probably a better way to do this without Pandas.

• If the np.cross part left you scratching your head, this is simply to find the minimum distance between a point and a line. I can followup with more detail if you're interested, but if you draw a cross product of two lines you get a parallelogram where the two non-parallel sides are given by the lines. This parallelogram has the same area as a rectangle with length equal to one of the lines, and width equal to the distance from the point to the line.

Answer 3

First find the Oriented Bounding Box (OBB) for the point cloud. There are several algorithms for that. This one is probably optimal:

https://pdfs.semanticscholar.org/a76f/7da5f8bae7b1fb4e85a65bd3812920c6d142.pdf

Now, a non-optimal oriented cylinder enclosing the OBB can easily be found by spinning the OBB around his longest axis. Similarly the cylinder enclosed by the OBB can be found as having the same axis as the other but radius is half the shortest side of the OBB face normal to the axis.

My conjeture is that the optimal cylinder radius is between these two cylinders.

The best cylinder can found easily if you calculate the min distance of all points to the outer cylinder and adjust the radius of it to make that distance equal to zero.

This approach probably works but is not computationally optimal, since you have to compute the distance from all points to cylinder. Maybe the inner cylinder may be used to cull all points that are inside of it. I have not elaborated too much that idea.

UPDATE:

It seem that the question is not clear about what is "smallest" and actually is requiring things beyond "smallest" and it is not well posed. The "smallest" cylinder enclosing a cloud of points is supposed to minimize the empty space inside the cylinder (at least I understand that as smallest). But the OP is also imposing the constraint that the smallest cylinder should fit the shape of input data. That means that if input data is sampling half of a cylinder (cut by its lonest side), the answer should be the cylinder that best fit the shape of that half. No matter if that cylinder has more empty space than other cylinder that encloses the data.

The two requierements are contradicting. Since the smallest cylinder may not fit the curved shape of the data and the cylinder best fitting the curved shape of the data could not be the smallest cylinder.

My answer (and other answers) based on OBB does answer the question with respect to "smallest" cylinder enclosing the data minimizing empty space inside the cylinder.

The other case of fitting the cylinder to the shape of the data can also be answered using an optimization approach. But there is no general answer. The "best" cylinder depends on the application needs and has to computed with at least two different strategies depending on the data.

Answer 4

Finding the exact solution seems a very difficult problem. By making hypotheses on the axis direction, and by rotating the cloud (of which you only keep the vertices of the convex hull) and projecting the points onto XY, you can indeed turn to a minimal enclosing circle problem.

But you have to make several hypothesis on the possible directions. For the exact solution, you should try all the directions such that the enclosing circle is defined by different pairs or triples of vertices. This defines complex regions in the space of the rotation angles, and for every region there is a point that achieves an optimimum. This involves a highly nonlinear minimization problem with nonlinear constraints, and seems barely tractable.

At this stage, all I can recommend is an approximate solution such that you try a fixed number of predefined directions and solve the corresponding circle fit. As the solution is approximate anyway, an approximate circle fit can do as well.

Answer 5

Brute-force algorith

Let's start with the most simple case: 3 points.

The smallest cylinder has the three points in its surface. The smallest radius means that two points are in the diameter of a cross-section, even if that section is not perpendicular to the axis of the cylinder. Same goes for the third point.
So the axis goes through the center of the diameter, which is the middle-point of the segment defined by two points.
Thus, the axis is defined by two middle points.

We have three middle points, and three possible axis:

The best solution (minimum radius) is chosen by finding the minimum ri among the solutions.

Note that each axis ai is parallel to some Pi,Pj segment.

GENERIC, n POINTS CASE

Let's say we have found the solution. At least three points of this solution lie in the surface, which is similar to the 3-points case. If we find that triplet, then we can apply the middle-points method.
Thus, the axis for the solution is some line through two middle points. In this brute-force algorithm we test them all. For each axis, compute the distance of all points perpendicular to that axis and get the largest, di, so we get the enclosing radius for each axis.

The solution is the axis for the minimum di. The radius is this minimum di.

Which is the order of this algorithm?
For n points we have C(n,2)= n(n-1)/2 middle points. And n(n-1)(n(n-1)-2)/8 axis. For each axis we test n radius. So we get O(n⁵)

Improvements

• Build first the convex hull and discard all internal points
• I have the feeling that the axis for the solution is defined by longest Mi,Mj segment.

---

EDIT

As @JRP showed, this method doesn't find the optimal solution for a prism. Trying with centers of triangles (instead of middle of segments) doesn't work neither, think of a point cloud with 8 points in a cube vertices.

It may be a good aproximation, but not the optimal solution.

Answer 6

First do a linear regression, for example by Ordinary least squares. This will give you the axis of the cylinder.

Now compute all distances from every point perpendicular to that 3D axis. The maximum value is the radius of the cylinder.

If in the process of computing the perpendicular distances you also get aligned distances inside the axis (put an origin some where far away), then the minimum and maximum aligned distances are those for top and bottom faces.