Facing ValueError: Target is multiclass but average='binary'

Question

I'm trying to use Naive Bayes algorithm for my dataset. I'm able to find out the accuracy but trying to find out precision and recall for the same. But, it is throwing the following error:

ValueError: Target is multiclass but average='binary'. Please choose another average setting.

Can anyone please suggest me how to proceed with it. I have tried using average ='micro' in the precision and the recall scores. It worked without any errors but it is giving the same score for accuracy, precision, recall.

My dataset:

train_data.csv:

review,label
Colors & clarity is superb,positive
Sadly the picture is not nearly as clear or bright as my 40 inch Samsung,negative

test_data.csv:

review,label
The picture is clear and beautiful,positive
Picture is not clear,negative

My code:

import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import confusion_matrix

X_train, y_train = pd.read_csv('train_data.csv')
X_test, y_test = pd.read_csv('test_data.csv')

vec = CountVectorizer() 
X_train_transformed = vec.fit_transform(X_train) 
X_test_transformed = vec.transform(X_test)

clf = MultinomialNB()
clf.fit(X_train_transformed, y_train)

score = clf.score(X_test_transformed, y_test)

y_pred = clf.predict(X_test_transformed)
cm = confusion_matrix(y_test, y_pred)

precision = precision_score(y_test, y_pred, pos_label='positive')
recall = recall_score(y_test, y_pred, pos_label='positive')

Answer 1

You need to add the 'average' param. According to the documentation:

average : string, [None, ‘binary’ (default), ‘micro’, ‘macro’, ‘samples’, ‘weighted’]

This parameter is required for multiclass/multilabel targets. If None, the scores for each class are returned. Otherwise, this determines the type of averaging performed on the data:

Do this:

print("Precision Score : ",precision_score(y_test, y_pred, 
                                           pos_label='positive'
                                           average='micro'))
print("Recall Score : ",recall_score(y_test, y_pred, 
                                           pos_label='positive'
                                           average='micro'))

Replace 'micro' with any one of the above options except 'binary'. Also, in the multiclass setting, there is no need to provide the 'pos_label' as it will be anyways ignored.

Update for comment:

Yes, they can be equal. Its given in the user guide here:

Note that for “micro”-averaging in a multiclass setting with all labels included will produce equal precision, recall and F, while “weighted” averaging may produce an F-score that is not between precision and recall.

Answer 2

The error is pretty self-explanatory. It is saying for a problem with more than 2 classes, there needs to be some kind of averaging rule. The valid rules are: 'micro', 'macro', 'weighted' and None (the documentation lists 'samples' but it's not applicable for multi-class targets).

If we look at its source code, multi-class problems are treated like a multi-label problem when it comes to precision and recall score computation because the underlying confusion matrix used (multilabel_confusion_matrix) is the same.¹ This confusion matrix creates a 3D array where each "sub-matrix" is the 2x2 confusion matrix where the positive value is one of the labels.

What are the differences between each averaging rule?

• With average=None, the precision/recall scores of each class is returned (without any averaging), so we get an array of scores whose length is equal to the number of classes.²

• With average='macro', precision/recall is computed for each class and then the average is taken. Its formula is as follows:

  

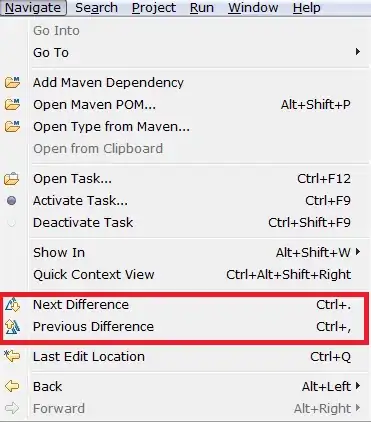
• With average='micro', the contributions of all classes are summed up to compute the average precision/recall. Its formula is as follows:

  

• average='weighted' is really a weighted macro average where the weights are the actual positive classes. Its formula is as follows:

  

---

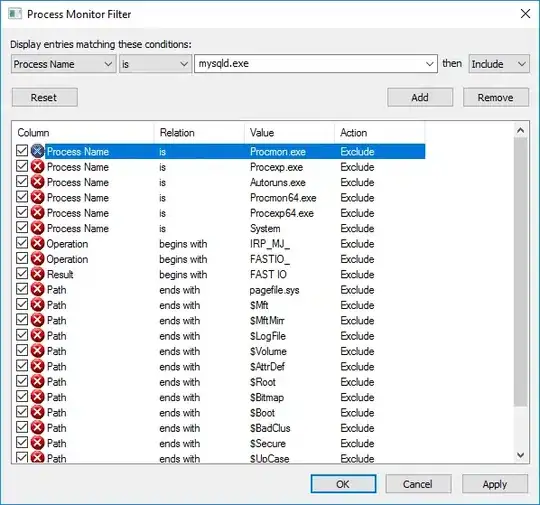
Let's consider an example.

import numpy as np
from sklearn import metrics
y_true, y_pred = np.random.default_rng(0).choice(list('abc'), size=(2,100), p=[.8,.1,.1])
mcm = metrics.multilabel_confusion_matrix(y_true, y_pred)

The multilabel confusion matrix computed above looks like the following.

The respective precision/recall scores are as follows:

• average='macro' precision/recall are:

  recall_macro = (57 / (57 + 16) + 1 / (1 + 10) + 6 / (6 + 10)) / 3
  precision_macro = (57 / (57 + 15) + 1 / (1 + 13) + 6 / (6 + 8)) / 3
  
  # verify using sklearn.metrics.precision_score and sklearn.metrics.recall_score
  recall_macro == metrics.recall_score(y_true, y_pred, average='macro')        # True
  precision_macro == metrics.precision_score(y_true, y_pred, average='macro')  # True
  

• average='micro' precision/recall are:

  recall_micro = (57 + 1 + 6) / (57 + 16 + 1 + 10 + 6 + 10)
  precision_micro = (57 + 1 + 6) / (57 + 15 + 1 + 13 + 6 + 8)
  
  # verify using sklearn.metrics.precision_score and sklearn.metrics.recall_score
  recall_micro == metrics.recall_score(y_true, y_pred, average='micro')        # True
  precision_micro == metrics.precision_score(y_true, y_pred, average='micro')  # True
  

• average='weighted' precision/recall are:

  recall_weighted = (57 / (57 + 16) * (57 + 16) + 1 / (1 + 10) * (1 + 10) + 6 / (6 + 10) * (6 + 10)) / (57 + 16 + 1 + 10 + 6 + 10)
  precision_weighted = (57 / (57 + 15) * (57 + 16) + 1 / (1 + 13) * (1 + 10) + 6 / (6 + 8) * (6 + 10)) / (57 + 16 + 1 + 10 + 6 + 10)
  
  # verify using sklearn.metrics.precision_score and sklearn.metrics.recall_score
  recall_weighted == metrics.recall_score(y_true, y_pred, average='weighted')        # True
  precision_weighted == metrics.precision_score(y_true, y_pred, average='weighted')  # True
  

As you can see, the example here is imbalanced (class a has 80% frequency while b and c have 10% each). The main difference between the averaging rules is that 'macro'-averaging doesn't account for class imbalance but 'micro' and 'weighted' do. So 'macro' is sensitive to the class imbalance and may result in an "artificially" high or low score depending on the imbalance.

Also, it's very easy to see from the formula that recall scores for 'micro' and 'weighted' are equal.

Why is accuracy == recall == precision == f1-score for average='micro'?

It may be easier to understand it visually.

If we look at the multilabel confusion matrix as constructed above, each sub-matrix corresponds to a One vs Rest classification problem; i.e. in each not column/row of a sub-matrix, the other two labels are accounted for.

For example, for the first sub-matrix, there are

• 57 true positives (a)
• 16 false negatives (either b or c)
• 15 false positives (either b or c)
• 12 true negatives

For the computation of precision/recall, only TP, FN and FP matter. As detailed above, FN and FP counts could be either b or c; since it is binary, this sub-matrix, by itself, cannot say how many of each is predicted; however, we can determine exactly how many of each were correctly classified by computing a multiclass confusion matrix by simply calling the confusion_matrix() method.

mccm = metrics.confusion_matrix(y_true, y_pred)

The following graph plots the same confusion matrix (mccm) using different background colors (yellow background corresponds to TP, red background corresponds to false negatives in the first sub-matrix, orange correspond to false positives in the third sub-matrix etc.). So these are actually TP, FN and FP in the multilabel confusion matrix "expanded" to account for exactly what was the negative class. The color scheme on the left graph matches the colors of TP and FN counts in the multilabel confusion matrix (those used to determine recall) and the color scheme on the right graph matches the colors of TP and FP (those used to determine precision).

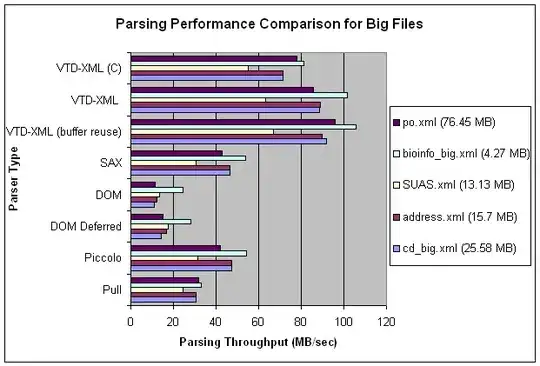
With average='micro', the ratio of yellow background numbers and all numbers in the left graph determine recall and the yellow background numbers and all numbers in the right graph determine precision. If we look closely the same ratio also determines accuracy. Moreover, since f1-score is the harmonic mean of precision and recall and given they are equal, we have the relationship recall == precision == accuracy == f1-score.