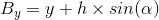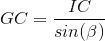Get bounds of unrotated rotated rectangle

Question

I have a rectangle that has a rotation already applied to it. I want to get the the unrotated dimensions (the x, y, width, height).

Here is the dimensions of the element currently:

Bounds at a 90 rotation: {
 height     30
 width      0
 x          25
 y          10
}

Here are the dimensions after the rotation is set to none:

Bounds at rotation 0 {
 height     0
 width      30
 x          10
 y          25
}

In the past, I was able to set the rotation to 0 and then read the updated bounds . However, there is a bug in one of the functions I was using, so now I have to do it manually.

Is there a simple formula to get the bounds at rotation 0 using the info I already have?

Update: The object is rotated around the center of the object.

UPDATE:
What I need is something like the function below:

function getRectangleAtRotation(rect, rotation) {
    var rotatedRectangle = {}
    rotatedRectangle.x = Math.rotation(rect.x * rotation);
    rotatedRectangle.y = Math.rotation(rect.y * rotation);
    rotatedRectangle.width = Math.rotation(rect.width * rotation);
    rotatedRectangle.height = Math.rotation(rect.height * rotation);
    return rotatedRectangle;
}

var rectangle = {x: 25, y: 10, height: 30, width: 0 };
var rect2 = getRectangleAtRotation(rect, -90); // {x:10, y:25, height:0, width:30 }

I found a similar question here.

UPDATE 2
Here is the code I have. It attempts to get the center point of the line and then the x, y, width, and height:

var centerPoint = getCenterPoint(line);
var lineBounds = {};
var halfSize;

halfSize = Math.max(Math.abs(line.end.x-line.start.x)/2, Math.abs(line.end.y-line.start.y)/2);
lineBounds.x = centerPoint.x-halfSize;
lineBounds.y = centerPoint.y;
lineBounds.width = line.end.x;
lineBounds.height = line.end.y;

function getCenterPoint(node) {
    return {
        x: node.boundsInParent.x + node.boundsInParent.width/2,
        y: node.boundsInParent.y + node.boundsInParent.height/2
    }
}

I know the example I have uses a right angle and that you can swap the x and y with that but the rotation can be any amount.

UPDATE 3

I need a function that returns the unrotated bounds of a rectangle. I have the bounds at a specific rotation already.

function getUnrotatedRectangleBounds(rect, currentRotation) {
    // magic
    return unrotatedRectangleBounds;
}

Answer 1

I think I can handle the calculation of the bounds size without too much effort (few equations), I'm not sure, instead, how you would like x and y to be handled.

First, let's properly name things:

Now, we want to rotate it by some angle alpha (in radians):

To calculate the green sides, it is clear that it's made of two repeated rectangle-triangles as the following:

So, solving angles first, we know that:

1. the sum of the angles of a triangle is PI, or 180°;
2. the rotation is alpha;
3. one angle gamma is PI / 2, or 90°;
4. the last angle, beta, is gamma - alpha;

Now, knowing all the angles and a side, we can use the Law of Sines to calculate other sides.

As a brief recap, the Law of Sines tells us that there is an equality between the ratio of a side length and it's opposite angle. More info here: https://en.wikipedia.org/wiki/Law_of_sines

In our case, for the upper left triangle (and the bottom right one), we have:

Remember that AD is our original height.

Given that the sin(gamma) is 1, and we also know the value of AD, we can write the equations:

For the upper right triangle (and the bottom left one), we then have:

Having all needed sides, we can easily calculate the width and height:

width = EA + AF
height = ED + FB

At this point we can write a quite easy method that, given a rectangle and a rotation angle in radians, can return new bounds:

function rotate(rectangle, alpha) {
  const { width: AB, height: AD } = rectangle
  const gamma = Math.PI / 4,
        beta = gamma - alpha,
        EA = AD * Math.sin(alpha),
        ED = AD * Math.sin(beta),
        FB = AB * Math.sin(alpha),
        AF = AB * Math.sin(beta)

  return {
    width: EA + AF,
    height: ED + FB
  }
}

This method can then be used like:

const rect = { width: 30, height: 50 }
const rotation = Math.PI / 4.2 // this is a random value it put here
const bounds = rotate(rect, rotation)

Hope there aren't typos...

Answer 2

I think I might get a solution but, for safety, I prefer to prior repeat what we have and what we need to be sure I understood everything correctly. As I said in a comment, english isn't my native language and I already wrote a wrong answer due to my lack of understanding of the problem :)

What we have

We know that at x and y there is a bounds rectangle (green) of size w and h that contains another rectangle (the grey dotted one) rotated of alpha degrees.

We know that the y axis is flipped relatively to the Cartesian one, and that makes the angle to be considered clockwise instead of counter-clockwise.

What we need

At first, we need to find the 4 vertices of the inner rectangle (A, B, C and D) and, knowing the position of the vertices, the size of the inner rectangle (W and H).

As a second step, we need to counter rotate the inner rectangle to 0 degrees, and find it's position X and Y.

Find the vertices

Generally speaking for each vertex we know only one coordinate, the x or the y. The other one "slides" along the side of the bounding box in relation to the angle alpha.

Let's start with A: we know Ay, we need Ax.

We know that the Ax lies between x and x + w in relation to the angle alpha.

When alpha is 0°, Ax is x + 0. When alpha is 90°, Ax is x + w. When alpha is 45°, Ax is x + w / 2.

Basically, Ax grows in relation of the sin(alpha), giving us:

Having Ax, we can easily compute Cx:

In the same way we can compute By and then Dy:

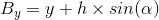
Writing some code:

// bounds is a POJO with shape: { x, y, w, h }, update if needed
// alpha is the rotation IN RADIANS
const vertices = (bounds, alpha) => {
  const { x, y, w, h } = bounds,
        A = { x: x + w * Math.sin(alpha), y },
        B = { x, y: y + h * Math.sin(alpha) },
        C = { x: x + w - w * Math.sin(alpha), y },
        D = { x, y: y + h - h * Math.sin(alpha) }
  return { A, B, C, D }
}

Finding the sides

Now that we have all the vertices, we can easily compute the inner rectangle sides, we need to define a couple more points E and F for clarity of explanation:

Its clearly visible that we can use the Pitagorean Theorem to compute W and H with:

where:

In code:

// bounds is a POJO with shape: { x, y, w, h }, update if needed
// vertices is a POJO with shape: { A, B, C, D }, as returned by the `vertices` method
const sides = (bounds, vertices) => {
  const { x, y, w, h } = bounds,
        { A, B, C, D } = vertices,
        EA = A.x - x,
        ED = D.y - y,
        AF = w - EA,
        FB = h - ED,
        H = Math.sqrt(EA * EA + ED * ED),
        W = Math.sqrt(AF * AF + FB * FB
  return { h: H, w: W }
}

Finding the position of the counter-rotated inner rectangle

First of all, we have to find the angles (beta and gamma) of the diagonals of the inner rectangle.

Let's zoom in a little bit and add some additional letters for more clarity:

We can use the Law of Sines to get the equations to compute beta:

To make some calculations we have:

We need to compute GC first in order to have at least one side of the equation completely known. GC is the radius of the circumference the inner rectangle is inscribed in and also half of the inner rectangle diagonal.

Having the two sides of the inner rectangle, we can use the Pitagorean Theorem again:

With GC we can solve the Law of Sines on beta:

we know that sin(delta) is 1

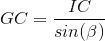
Now, beta is the angle of the vertex C in relation with the unrotated x axis.

Looking again at this image, we can easily get the angles of all the other vertices:

Now that we have almost everything, we can compute the new coordinates of the A vertex:

From here, we need to translate both Ax and Ay because they are related to the center of the circumference, which is x + w / 2 and y + h / 2:

So, writing the last piece of code:

// bounds is a POJO with shape: { x, y, w, h }, update if needed
// sides is a POJO with shape: { w, h }, as returned by the `sides` method
const origin = (bounds, sides) => {
  const { x, y, w, h } = bounds
  const { w: W, h: H } = sides
  const GC = r = Math.sqrt(W * W + H * H) / 2,
        IC = H / 2,
        beta = Math.asin(IC / GC),
        angleA = Math.PI + beta,
        Ax = x + w / 2 + r * Math.cos(angleA),
        Ay = y + h / 2 + r * Math.sin(angleA)
  return { x: Ax, y: Ay }
}

Putting all together...

// bounds is a POJO with shape: { x, y, w, h }, update if needed
// rotations is... the rotation of the inner rectangle IN RADIANS
const unrotate = (bounds, rotation) => {
  const points = vertices(bounds, rotation),
        dimensions = sides(bounds, points)
  const { x, y } = origin(bounds, dimensions)
  return { ...dimensions, x, y }
}

I really hope this will solve your problem and that there are no typos. This was a very, veeeery funny way to spend my weekend :D

// bounds is a POJO with shape: { x, y, w, h }, update if needed
// alpha is the rotation IN RADIANS
const vertices = (bounds, alpha) => {
 const { x, y, w, h } = bounds,
    A = { x: x + w * Math.sin(alpha), y },
    B = { x, y: y + h * Math.sin(alpha) },
    C = { x: x + w - w * Math.sin(alpha), y },
    D = { x, y: y + h - h * Math.sin(alpha) }
 return { A, B, C, D }
 }
  
// bounds is a POJO with shape: { x, y, w, h }, update if needed
// vertices is a POJO with shape: { A, B, C, D }, as returned by the `vertices` method
const sides = (bounds, vertices) => {
  const { x, y, w, h } = bounds,
      { A, B, C, D } = vertices,
      EA = A.x - x,
      ED = D.y - y,
      AF = w - EA,
      FB = h - ED,
      H = Math.sqrt(EA * EA + ED * ED),
      W = Math.sqrt(AF * AF + FB * FB)
  return { h: H, w: W }
}

// bounds is a POJO with shape: { x, y, w, h }, update if needed
// sides is a POJO with shape: { w, h }, as returned by the `sides` method
const originPoint = (bounds, sides) => {
  const { x, y, w, h } = bounds
  const { w: W, h: H } = sides
  const GC = Math.sqrt(W * W + H * H) / 2,
      r = Math.sqrt(W * W + H * H) / 2,
      IC = H / 2,
      beta = Math.asin(IC / GC),
      angleA = Math.PI + beta,
      Ax = x + w / 2 + r * Math.cos(angleA),
      Ay = y + h / 2 + r * Math.sin(angleA)
  return { x: Ax, y: Ay }
}
  
// bounds is a POJO with shape: { x, y, w, h }, update if needed
// rotations is... the rotation of the inner rectangle IN RADIANS
const unrotate = (bounds, rotation) => {
  const points = vertices(bounds, rotation)
  const dimensions = sides(bounds, points)
  const { x, y } = originPoint(bounds, dimensions)
  return { ...dimensions, x, y }
}

function shortNumber(value) {
  var places = 2;
 value = Math.round(value * Math.pow(10, places)) / Math.pow(10, places);
 return value;
}

function getInputtedBounds() {
  var rectangle = {};
  rectangle.x = parseFloat(app.xInput.value);
  rectangle.y = parseFloat(app.yInput.value);
  rectangle.w = parseFloat(app.widthInput.value);
  rectangle.h = parseFloat(app.heightInput.value);
  return rectangle;
}

function rotationSliderHandler() {
  var rotation = app.rotationSlider.value;
  app.rotationOutput.value = rotation;
  rotate(rotation);
}

function rotationInputHandler() {
  var rotation = app.rotationInput.value;
  app.rotationSlider.value = rotation;
  app.rotationOutput.value = rotation;
  rotate(rotation);
}

function unrotateButtonHandler() {
  var rotation = app.rotationInput.value;
  app.rotationSlider.value = 0;
  app.rotationOutput.value = 0;
  var outerBounds = getInputtedBounds();
  var radians = Math.PI / 180 * rotation;
  var unrotatedBounds = unrotate(outerBounds, radians);
  updateOutput(unrotatedBounds);
}

function rotate(value) {
  var outerBounds = getInputtedBounds();
  var radians = Math.PI / 180 * value;
  var bounds = unrotate(outerBounds, radians);
  updateOutput(bounds);
}

function updateOutput(bounds) {
  app.xOutput.value = shortNumber(bounds.x);
  app.yOutput.value = shortNumber(bounds.y);
  app.widthOutput.value = shortNumber(bounds.w);
  app.heightOutput.value = shortNumber(bounds.h);
}

function onload() {
  app.xInput = document.getElementById("x");
  app.yInput = document.getElementById("y");
  app.widthInput = document.getElementById("w");
  app.heightInput = document.getElementById("h");
  app.rotationInput = document.getElementById("r");
  
  app.xOutput = document.getElementById("x2");
  app.yOutput = document.getElementById("y2");
  app.widthOutput = document.getElementById("w2");
  app.heightOutput = document.getElementById("h2");
  app.rotationOutput = document.getElementById("r2");
  app.rotationSlider = document.getElementById("rotationSlider");
  app.unrotateButton = document.getElementById("unrotateButton");
  
  app.unrotateButton.addEventListener("click", unrotateButtonHandler);
  app.rotationSlider.addEventListener("input", rotationSliderHandler);
  app.rotationInput.addEventListener("change", rotationInputHandler);
  app.rotationInput.addEventListener("input", rotationInputHandler);
  app.rotationInput.addEventListener("keyup", (e) => {if (e.keyCode==13) rotationInputHandler() });
  
  app.rotationSlider.value = app.rotationInput.value;
}

var app = {};
window.addEventListener("load", onload);

* {
  font-family: sans-serif;
  font-size: 12px;
  outline: 0px dashed red;
}

granola {
  display: flex;
  align-items: top;
}

flan {
  width: 90px;
  display: inline-block;
}

hamburger {
  display: flex:
  align-items: center;
}

spagetti {
  display: inline-block;
  font-size: 11px;
  font-weight: bold;
  letter-spacing: 1.5px;
}

fish {
  display: inline-block;
  padding-right: 40px;
  position: relative;
}

input[type=text] {
  width: 50px;
}

input[type=range] {
  padding-top: 10px;
  width: 140px;
  padding-left: 0;
  margin-left: 0;
}

button {
  padding-top: 3px;
  padding-bottom:1px;
  margin-top: 10px;
}

<granola>
  <fish>
    <spagetti>Bounds of Rectangle</spagetti><br><br>
    <flan>x: </flan><input id="x" type="text" value="14.39"><br>
    <flan>y: </flan><input id="y" type="text" value="14.39"><br>
    <flan>width: </flan><input id="w" type="text" value="21.2"><br>
    <flan>height: </flan><input id="h" type="text" value="21.2"><br>
    <flan>rotation:</flan><input id="r" type="text" value="90"><br>
    <button id="unrotateButton">Unrotate</button>    
  </fish>

  <fish>
    <spagetti>Computed Bounds</spagetti><br><br>
    <flan>x: </flan><input id="x2" type="text" disabled="true"><br>
    <flan>y: </flan><input id="y2" type="text"disabled="true"><br>
    <flan>width: </flan><input id="w2" type="text" disabled="true"><br>
    <flan>height: </flan><input id="h2" type="text" disabled="true"><br>
    <flan>rotation:</flan><input id="r2" type="text" disabled="true"><br>
    <input id="rotationSlider" type="range" min="-360" max="360" step="5"><br>
  </fish>
</granola>

Answer 3

How does this work?

Calculation using width, height, x and y

Radians and Angles

Using degrees calculate the radians and calculate the sin and cos angles:

function calculateRadiansAndAngles(){
  const rotation = this.value;
  const dr = Math.PI / 180;
  const s = Math.sin(rotation * dr);
  const c = Math.cos(rotation * dr);
  console.log(rotation, s, c);
}

document.getElementById("range").oninput = calculateRadiansAndAngles;

<input type="range" min="-360" max="360" id="range"/>

Generate 4 points

we assume the origin of a rectangle is the center with the location of 0,0

The double for loop will create the following value pairs for i and j: (-1,-1), (-1,1), (1,-1) and (1,1)

Using each pair, we can calculate one of the 4 square vectors.

(i.e for (-1,1), i = -1, j = 1)

const px = w*i/2; //-> 30 * -1/2 = -15
const py = h*j/2; //-> 50 * 1/2  = 25
//[-15,25]

Once we have a point, we can calculate the new position of that point by including the rotation.

const nx = (px*c) - (py*s);
const ny = (px*s) + (py*c);

Solution

Once all the points are calculated based off of the rotation, we can redraw our square.

Before the draw call, a translate is used to position the cursor at the x and y of the rectangle. This is the reason as to why I was able to assume the center and the origin of the rectangle was 0,0 for the calculations.

const canvas = document.getElementById("canvas");
const range = document.getElementById("range");
const rotat = document.getElementById("rotat");

range.addEventListener("input", function(e) {
  rotat.innerText = this.value;
  handleRotation(this.value);
})

const context = canvas.getContext("2d");
const container = document.getElementById("container");

const rect = {
  x: 50,
  y: 75,
  w: 30,
  h: 50
}

function handleRotation(rotation) {
  const { w, h, x, y } = rect;
  
  const dr = Math.PI / 180;
  const s = Math.sin(rotation * dr);
  const c = Math.cos(rotation * dr);
  
  const points = [];
  for(let i = -1; i < 2; i+=2){
    for(let j = -1; j < 2; j+=2){
      
      const px = w*i/2;
      const py = h*j/2;
      
      const nx = (px*c) - (py*s);
      const ny = (px*s) + (py*c);
      points.push([nx, ny]);
    }
  }
  //console.log(points);
  draw(points);
  
}

function draw(points) {
  context.clearRect(0,0,canvas.width, canvas.height);
  context.save();
  context.translate(rect.x+(rect.w/2), rect.y + (rect.h/2))
  context.beginPath();
  context.moveTo(...points.shift());
  [...points.splice(0,1), ...points.reverse()]
  .forEach(p=>{
    context.lineTo(...p);
  })
  context.fill();
  context.restore();
}

window.onload = () => handleRotation(0);

div {
  display: flex;
  background-color: lightgrey;
  padding: 0 5px;
}

div>p {
  padding: 0px 10px;
}

div>input {
  flex-grow: 1;
}

canvas {
  border: 1px solid black;
}

<div>
  <p id="rotat">0</p>
  <input type="range" id="range" min="-360" max="360" value="0" step="5" />
</div>
<canvas id="canvas"></canvas>

Answer 4

This is the basic code for a rectangle rotating(Unrotating is the same thing only with a negative angle) around its center.

function getUnrotatedRectangleBounds(rect, currentRotation) {

    //Convert deg to radians
    var rot = currentRotation / 180 * Math.PI;
    var hyp = Math.sqrt(rect.width * rect.width + rect.height * rect.height);
    return {
       x: rect.x + rect.width / 2 - hyp * Math.abs(Math.cos(rot)) / 2,
       y: rect.y + rect.height / 2 - hyp * Math.abs(Math.sin(rot)) / 2,
       width: hyp * Math.abs(Math.cos(rot)),
       height: hyp * Math.abs(Math.sin(rot))
       } 
}

The vector starting at the origin(0,0) and ending at (width,height) is projected onto a unit vector for the target angle (cos rot,sin rot) * hyp.

The absolute values guarantee the width and height are both positive.

The coordinates of the projection are the width and height, respectively, of the new rectangle.

For the x and y values, take the original values at the center(x + rect.x) and move it back out(- 1/2 * NewWidth) so it centers the new rectangle.

Example

function getUnrotatedRectangleBounds(rect, currentRotation) {
    //Convert deg to radians
    var rot = currentRotation / 180 * Math.PI;
    var hyp = Math.sqrt(rect.width * rect.width + rect.height * rect.height);
    return {
       x: rect.x + rect.width / 2 - hyp * Math.abs(Math.cos(rot)) / 2,
       y: rect.y + rect.height / 2 - hyp * Math.abs(Math.sin(rot)) / 2,
       width: hyp * Math.abs(Math.cos(rot)),
       height: hyp * Math.abs(Math.sin(rot))
    }
}

var originalRectangle = {x:10, y:25, width:30, height:0};
var rotatedRectangle = {x:14.39, y:14.39, width:21.2, height:21.2};
var rotation = 45;
var unrotatedRectangle = getUnrotatedRectangleBounds(rotatedRectangle, rotation);

var boundsLabel = document.getElementById("boundsLabel");
boundsLabel.innerHTML = JSON.stringify(unrotatedRectangle);

<span id="boundsLabel"></span>