Divide by 10 using bit shifts?

Question

Is it possible to divide an unsigned integer by 10 by using pure bit shifts, addition, subtraction and maybe multiply? Using a processor with very limited resources and slow divide.

Answer 1

Editor's note: this is not actually what compilers do, and gives the wrong answer for large positive integers ending with 9, starting with div10(1073741829) = 107374183 not 107374182 (Godbolt). It is exact for inputs smaller than 0x40000005, though, which may be sufficient for some uses.

Compilers (including MSVC) do use fixed-point multiplicative inverses for constant divisors, but they use a different magic constant and shift on the high-half result to get an exact result for all possible inputs, matching what the C abstract machine requires. See Granlund & Montgomery's paper on the algorithm.

See Why does GCC use multiplication by a strange number in implementing integer division? for examples of the actual x86 asm gcc, clang, MSVC, ICC, and other modern compilers make.

---

This is a fast approximation that's inexact for large inputs

It's even faster than the exact division via multiply + right-shift that compilers use.

You can use the high half of a multiply result for divisions by small integral constants. Assume a 32-bit machine (code can be adjusted accordingly):

int32_t div10(int32_t dividend)
{
    int64_t invDivisor = 0x1999999A;
    return (int32_t) ((invDivisor * dividend) >> 32);
}

What's going here is that we're multiplying by a close approximation of 1/10 * 2^32 and then removing the 2^32. This approach can be adapted to different divisors and different bit widths.

This works great for the ia32 architecture, since its IMUL instruction will put the 64-bit product into edx:eax, and the edx value will be the wanted value. Viz (assuming dividend is passed in ecx (fastcall) and quotient returned in eax)

div10 proc 
    mov    eax,1999999Ah    ; 1/10 * 2^32
    imul   ecx              ; edx:eax = dividend / 10 * 2 ^32
    mov    eax,edx          ; eax = dividend / 10
    ret
endp

Even on a machine with a slow multiply instruction, this will be faster than a software or even hardware divide.

Answer 2

Though the answers given so far match the actual question, they do not match the title. So here's a solution heavily inspired by Hacker's Delight that really uses only bit shifts.

unsigned divu10(unsigned n) {
    unsigned q, r;
    q = (n >> 1) + (n >> 2);
    q = q + (q >> 4);
    q = q + (q >> 8);
    q = q + (q >> 16);
    q = q >> 3;
    r = n - (((q << 2) + q) << 1);
    return q + (r > 9);
}

I think that this is the best solution for architectures that lack a multiply instruction.

Answer 3

Of course you can if you can live with some loss in precision. If you know the value range of your input values you can come up with a bit shift and a multiplication which is exact. Some examples how you can divide by 10, 60, ... like it is described in this blog to format time the fastest way possible.

temp = (ms * 205) >> 11;  // 205/2048 is nearly the same as /10

Answer 4

to expand Alois's answer a bit, we can expand the suggested y = (x * 205) >> 11 for a few more multiples/shifts:

y = (ms *        1) >>  3 // first error 8
y = (ms *        2) >>  4 // 8
y = (ms *        4) >>  5 // 8
y = (ms *        7) >>  6 // 19
y = (ms *       13) >>  7 // 69
y = (ms *       26) >>  8 // 69
y = (ms *       52) >>  9 // 69
y = (ms *      103) >> 10 // 179
y = (ms *      205) >> 11 // 1029
y = (ms *      410) >> 12 // 1029
y = (ms *      820) >> 13 // 1029
y = (ms *     1639) >> 14 // 2739
y = (ms *     3277) >> 15 // 16389
y = (ms *     6554) >> 16 // 16389
y = (ms *    13108) >> 17 // 16389
y = (ms *    26215) >> 18 // 43699
y = (ms *    52429) >> 19 // 262149
y = (ms *   104858) >> 20 // 262149
y = (ms *   209716) >> 21 // 262149
y = (ms *   419431) >> 22 // 699059
y = (ms *   838861) >> 23 // 4194309
y = (ms *  1677722) >> 24 // 4194309
y = (ms *  3355444) >> 25 // 4194309
y = (ms *  6710887) >> 26 // 11184819
y = (ms * 13421773) >> 27 // 67108869

each line is a single, independent, calculation, and you'll see your first "error"/incorrect result at the value shown in the comment. you're generally better off taking the smallest shift for a given error value as this will minimise the extra bits needed to store the intermediate value in the calculation, e.g. (x * 13) >> 7 is "better" than (x * 52) >> 9 as it needs two less bits of overhead, while both start to give wrong answers above 68.

if you want to calculate more of these, the following (Python) code can be used:

def mul_from_shift(shift):
    mid = 2**shift + 5.
    return int(round(mid / 10.))

and I did the obvious thing for calculating when this approximation starts to go wrong with:

def first_err(mul, shift):
    i = 1
    while True:
        y = (i * mul) >> shift
        if y != i // 10:
            return i
        i += 1

(note that // is used for "integer" division, i.e. it truncates/rounds towards zero)

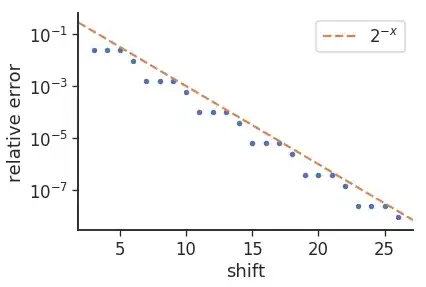
the reason for the "3/1" pattern in errors (i.e. 8 repeats 3 times followed by 9) seems to be due to the change in bases, i.e. log2(10) is ~3.32. if we plot the errors we get the following:

where the relative error is given by: mul_from_shift(shift) / (1<<shift) - 0.1

Answer 5

Considering Kuba Ober’s response, there is another one in the same vein.
It uses iterative approximation of the result, but I wouldn’t expect any surprising performances.

Let say we have to find x where x = v / 10.

We’ll use the inverse operation v = x * 10 because it has the nice property that when x = a + b, then x * 10 = a * 10 + b * 10.

Let use x as variable holding the best approximation of result so far. When the search ends, x Will hold the result. We’ll set each bit b of x from the most significant to the less significant, one by one, end compare (x + b) * 10 with v. If its smaller or equal to v, then the bit b is set in x. To test the next bit, we simply shift b one position to the right (divide by two).

We can avoid the multiplication by 10 by holding x * 10 and b * 10 in other variables.

This yields the following algorithm to divide v by 10.

uin16_t x = 0, x10 = 0, b = 0x1000, b10 = 0xA000;
while (b != 0) {
    uint16_t t = x10 + b10;
    if (t <= v) {
        x10 = t;
        x |= b;
    }
    b10 >>= 1;
    b >>= 1;
}
// x = v / 10

Edit: to get the algorithm of Kuba Ober which avoids the need of variable x10 , we can subtract b10 from v and v10 instead. In this case x10 isn’t needed anymore. The algorithm becomes

uin16_t x = 0, b = 0x1000, b10 = 0xA000;
while (b != 0) {
    if (b10 <= v) {
        v -= b10;
        x |= b;
    }
    b10 >>= 1;
    b >>= 1;
}
// x = v / 10

The loop may be unrolled and the different values of b and b10 may be precomputed as constants.

Answer 6

On architectures that can only shift one place at a time, a series of explicit comparisons against decreasing powers of two multiplied by 10 might work better than the solution form hacker's delight. Assuming a 16 bit dividend:

uint16_t div10(uint16_t dividend) {
  uint16_t quotient = 0;
  #define div10_step(n) \
    do { if (dividend >= (n*10)) { quotient += n; dividend -= n*10; } } while (0)
  div10_step(0x1000);
  div10_step(0x0800);
  div10_step(0x0400);
  div10_step(0x0200);
  div10_step(0x0100);
  div10_step(0x0080);
  div10_step(0x0040);
  div10_step(0x0020);
  div10_step(0x0010);
  div10_step(0x0008);
  div10_step(0x0004);
  div10_step(0x0002);
  div10_step(0x0001);
  #undef div10_step
  if (dividend >= 5) ++quotient; // round the result (optional)
  return quotient;
}

Answer 7

Well division is subtraction, so yes. Shift right by 1 (divide by 2). Now subtract 5 from the result, counting the number of times you do the subtraction until the value is less than 5. The result is number of subtractions you did. Oh, and dividing is probably going to be faster.

A hybrid strategy of shift right then divide by 5 using the normal division might get you a performance improvement if the logic in the divider doesn't already do this for you.

Answer 8

I've designed a new method in AVR assembly, with lsr/ror and sub/sbc only. It divides by 8, then sutracts the number divided by 64 and 128, then subtracts the 1,024th and the 2,048th, and so on and so on. Works very reliable (includes exact rounding) and quick (370 microseconds at 1 MHz). The source code is here for 16-bit-numbers: http://www.avr-asm-tutorial.net/avr_en/beginner/DIV10/div10_16rd.asm The page that comments this source code is here: http://www.avr-asm-tutorial.net/avr_en/beginner/DIV10/DIV10.html I hope that it helps, even though the question is ten years old. brgs, gsc

Answer 9

elemakil's comments' code can be found here: https://doc.lagout.org/security/Hackers%20Delight.pdf page 233. "Unsigned divide by 10 [and 11.]"