Two-color Path object

Question

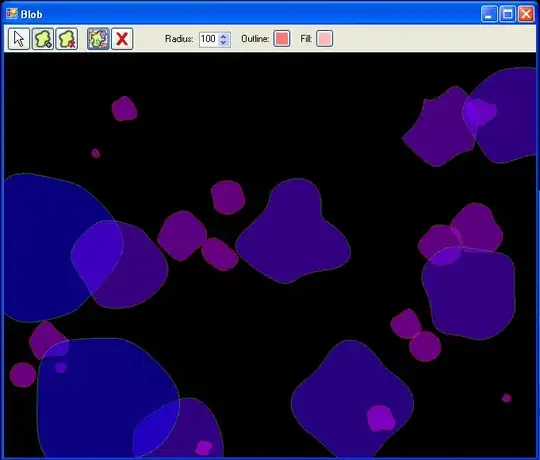
The following image illustrates what I am trying to achieve:

Basically I want to create two Path objects that "touch" each other (parallel paths). This is XAML used to generate this image:

<StackPanel Orientation="Horizontal">
    <StackPanel.LayoutTransform>
        <ScaleTransform CenterX="0" CenterY="0" ScaleX="15" ScaleY="15" />
    </StackPanel.LayoutTransform>
    
    <Grid Margin="-5,0,0,0">
        <Path Stroke="Blue">
            <Path.Data>
                <PathGeometry>M10,10 C20,10 10,20 20,20</PathGeometry>
            </Path.Data>
        </Path>
        <Path Stroke="Red">
            <Path.Data>
                <PathGeometry>M10,11 C19,10.85 9,20.80 20,21</PathGeometry>
            </Path.Data>
        </Path>
    </Grid>
    
    <Grid Margin="-5,0,0,0">
        <Path Stroke="Blue">
            <Path.Data>
                <PathGeometry>M10,10 C20,10 10,20 20,20</PathGeometry>
            </Path.Data>
        </Path>
        <Path Stroke="Red">
            <Path.Data>
                <PathGeometry>M10,11 C19,11 9,21 20,21</PathGeometry>
            </Path.Data>
        </Path>
    </Grid>
</StackPanel>

The first curve has hand-optimized point positions, the second has point positions easily calculated by taking stroke thickness into consideration. You can see the second curve is not perfect, because there is a space between the two. How can I create two perfectly "touching" curves programmatically, without hand-optimizing every curve (which is actually not possible because the curves are generated in code)?

Simply put, I generate one curve (resp. Path) in code, and I need it to have two colors. So I thought making second parallel Path would do the trick, but adjusting Geometry of the second Path (to make it parallel) has proven to be problematic.

Update #1

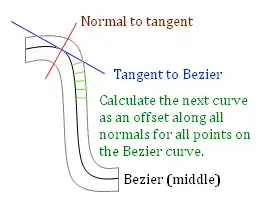
Parallel Lines and Curves by Charles Petzold might be one way to solve this problem. It actually works pretty well, but it flattens the curves, which creates visual artifacts when deeply zoomed, and of course there is a performance drawback.

The algorithm does not, however, attempt to find a Bézier curve that is parallel to another Bézier curve. The algorithm is instead based entirely on polylines: The input is one or more polylines and the output consists of multiple polylines for each input polyline. For this reason, ParallelPath needs to "flatten" the input geometry—which means converting the entire geometry (including arcs and Bézier curves) into a polyline approximation.

Update #2

So a friend of mine (math Ph.D. inceptor) has analyzed this problem and creating parallel curve to the (third-order) Bézier curve is very complex and computationally expensive. For each point of the parallel curve, computer would have to compute something like this:

(degree 3 polynomial) + (degree 2 polynomial) / sqrt(degree 4 polynomial)

Maybe there is a way to optimize this expression, but it would still be MUCH MORE computationally expensive than a standard Bézier curve (because the parallel curve is completely different curve than the original Bézier curve). I want to be able to animate the curve, so this solution would be probably too much CPU expensive. This leaves us with a couple of options:

1. Use Charles Petzold's polyline approximation, which works wonders, but there are visual glitches when deeply zoomed.

2. Derive our own approximation based on Charles Petzond's one. Use Bézier curves instead of lines (maybe arcs would be enough). This would solve the deep zoom problem, but it's probably quite hard to code (I have no clue how to do this).

3. Maybe it is possible to create something like two-color brush. This way, we could use just a single Path to achieve desired result (as shown by the first image). I haven't seen it anywhere though, so this is probably not an option.

Update #3

I've found some pretty interesting links:

• How to offset a cubic bezier curve? (Heuristic algorithm)
• Outline of cubic bezier curve stroke
• bezier path widening (Python algorithm)
• Offset Bézier Curves (Java implementation of custom polyline Bézier curve approximation; implementation differs from the Charles Petzold's one)
• Parallel Bézier (Why parallel Bézier curves are not possible from math point of view)
• Fast, precise flattening of cubic Bézier path and offset curves paper (Download link 1, Download link 2)

More info:

• QPainterPathStroker from Qt framework is supposed to be using the Thomas F. Hain's algorithm for parallel curves
• This Java Stroker is also supposed to be capable of drawing parallel curves

Maybe the final solution? (source here)

... I worked out all I knew about Bezier curve theory, and developed the unflattened offsetting to something that is correct, and (monster) documented that on A primer on Bezier curves

---

Attempt #1

Make second path a bit wider, and slide it underneath the first path while using Z-Index. http://i51.tinypic.com/2r5vwjk.png

This won't work, the Geometry must be transformed accordingly.

Answer 1

Instead of using one fourth-degree Bezier curve, why don't you just use a compund of two quadratic ones? Are you familiar with Bezier curve mathematics? They are favored in graphics because they are quite computationally cheap. I recently created a program where I animated cell movement (just for fun):

The program could easily run in fullscreen on an HD monitor with 100 blobs animated and moving about. And it was all GDI+.

As for parallel Bezier curves, according to Wikipedia it can't really be done: http://en.wikipedia.org/wiki/B%C3%A9zier_curve

So you'll probably have to be happy with an heuristic approach.

EDIT 1:

Lest your curves are completely random, why not create the outline of each curve and then fill the path? The "bottom" curve of one path will be the "top" curve of the other.

EDIT 2:

Ok, as requested, here's how I envision that a "railroadtrack-like" solution can be calculated:

Answer 2

You said you want to create two Path objects that touch each other, but you didn’t state how the paths are generated. My answer will assume that you have a Path already generated by some algorithm, and you want to turn this into two new paths.

I would switch from trying to use strokes to using fills. If you can automatically create the red path in your second picture, you can equally create a joined path consisting of both and then fill it instead of drawing it with a stroke. Then you do the same thing in two directions.

The result I get for your example looks like this:

<StackPanel Orientation="Horizontal">
    <StackPanel.LayoutTransform>
        <ScaleTransform CenterX="0" CenterY="0" ScaleX="15" ScaleY="15" />
    </StackPanel.LayoutTransform>

    <Grid Margin="-5,0,0,0">
        <Path Fill="Blue" Stroke="Transparent">
            <Path.Data>
                <PathGeometry>M10,10 C20,10 10,20 20,20 L20,19 C11,19 21,9 10,9</PathGeometry>
                <!--          |←    original path    →| |←  generated part   →| -->
            </Path.Data>
        </Path>
        <Path Fill="Red" Stroke="Transparent">
            <Path.Data>
                <PathGeometry>M10,10 C20,10 10,20 20,20 L20,21 C9,21 19,11 10,11</PathGeometry>
                <!--          |←    original path    →| |←   generated part   →| -->
            </Path.Data>
        </Path>
    </Grid>
</StackPanel>

Answer 3

Consider a slightly different approach to the problem...

Assuming a 'large' number of points on the geometry. It may be feasible to use one of the higher quality interpolaton methods by sampling the geometry points at lower zoom levels. As the zoom increases you can increase the sampling rate and instead render only a subset of the curve; This way the amount of computation should stays relatively constant at all zoom levels. The key is that there is a constant number of pixels on the screen and you can start sampling points once accuracy passes some threshold.

Answer 4

Read this... Silverlight - Epic Graphical Fail (rectangle by two triangles) :(

Update

Try this (it's little overkilling but it may help you)

<Grid Margin="-5,0,0,0">
    <Path Stroke="Blue" Data="M10,10 C20,10 10,20 20,20 M20,21 C9,21 19,11 10,11"
            Fill="Blue" Clip="M10,10 C20,10 10,20 20,20 L20,21 C9,21 19,11 10,11"/>
    <Path Stroke="Blue" Data="M10,10 C20,10 10,20 20,20"/>
    <Path Stroke="Red" Data="M10,11 C19,11 9,21 20,21"/>
</Grid>

Answer 5

Is it possible to make the second path(generated) a bit wider and slide it underneath (behind) the first path using the z-index? You'll get a seamless join that way.

Answer 6

Lets say you need two lines of width 5:

If one pixel of difference is not too much you could first draw a curve with let's say width 11 in red, then draw a curve with same path with width 1 in blue, then fill one of the sides with blue.

You would have split the line at half and colored one half, problem is that the splitting in half takes one pixel :(

But what would happen if you chose an even width like 10? Where would the middle pixel be? Maybe you can exploit something...