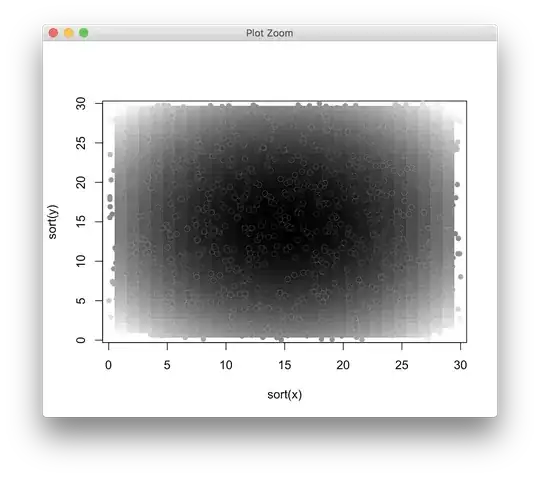
I have data in the form (x, y, z) where x and y are not on a regular grid. I wish to display a 2D colormap of these data, with intensity (say, grey scale) mapped to the z variable. An obvious solution is to interpolate (see below) on a regular grid,
d <- data.frame(x=runif(1e3, 0, 30), y=runif(1e3, 0, 30))
d$z = (d$x - 15)^2 + (d$y - 15)^2
library(akima)
d2 <- with(d, interp(x, y, z, xo=seq(0, 30, length = 30),
yo=seq(0, 30, length = 50), duplicate="mean"))
pal1 <- grey(seq(0,1,leng=500))
with(d2, image(sort(x), sort(y), z, useRaster=TRUE, col = pal1))
points(d$x, d$y, col="white", bg=grey(d$z/max(d$z)), pch=21, cex=1,lwd=0.1)
However, this loses the information of the initial mesh (position of the points with actual data), which could be very fine or very rough at certain locations. My preference would be for a delaunay tiling with triangles, which accurately represents the actual location and density of the original data points.
Ideally the solution would
compute the tesselation outside of the plotting function, so that the resulting polygons may be plotted with either
ggplot2,lattice, or base graphicsbe fast. In my real-life example (~1e5 points), the calculation of the tesselation via
deldircan be really slow.
By "tesselation" I mean either Delaunay triangles or Voronoi diagrams, although my preference would be for the former. However it bring the additional complexity of interpolating the colour of each triangle based on the original data points.