Calculate largest inscribed rectangle in a rotated rectangle

Question

I'm trying to find the best way to calculate the biggest (in area) rectangle which can be contained inside a rotated rectangle.

Some pictures should help (I hope) in visualizing what I mean:

The width and height of the input rectangle is given and so is the angle to rotate it. The output rectangle is not rotated or skewed.

I'm going down the longwinded route which I'm not even sure if it will handle the corner cases (no pun intended). I'm certain there is an elegant solution to this. Any tips?

EDIT: The output rectangle points don't necessarily have to touch the input rectangles edges. (Thanks to Mr E)

Answer 1

I just came here looking for the same answer. After shuddering at the thought of so much math involved, I thought I would resort to a semi-educated guess. Doodling a bit I came to the (intuitive and probably not entirely exact) conclusion that the largest rectangle is proportional to the outer resulting rectangle, and its two opposing corners lie at the intersection of the diagonals of the outer rectangle with the longest side of the rotated rectangle. For squares, any of the diagonals and sides would do... I guess I am happy enough with this and will now start brushing the cobwebs off my rusty trig skills (pathetic, I know).

Minor update... Managed to do some trig calculations. This is for the case when the Height of the image is larger than the Width.

Update. Got the whole thing working. Here is some js code. It is connected to a larger program, and most variables are outside the scope of the functions, and are modified directly from within the functions. I know this is not good, but I am using this in an isolated situation, where there will be no confusion with other scripts: redacted

---

I took the liberty of cleaning the code and extracting it to a function:

function getCropCoordinates(angleInRadians, imageDimensions) {
    var ang = angleInRadians;
    var img = imageDimensions;

    var quadrant = Math.floor(ang / (Math.PI / 2)) & 3;
    var sign_alpha = (quadrant & 1) === 0 ? ang : Math.PI - ang;
    var alpha = (sign_alpha % Math.PI + Math.PI) % Math.PI;

    var bb = {
        w: img.w * Math.cos(alpha) + img.h * Math.sin(alpha),
        h: img.w * Math.sin(alpha) + img.h * Math.cos(alpha)
    };

    var gamma = img.w < img.h ? Math.atan2(bb.w, bb.h) : Math.atan2(bb.h, bb.w);

    var delta = Math.PI - alpha - gamma;

    var length = img.w < img.h ? img.h : img.w;
    var d = length * Math.cos(alpha);
    var a = d * Math.sin(alpha) / Math.sin(delta);

    var y = a * Math.cos(gamma);
    var x = y * Math.tan(gamma);

    return {
        x: x,
        y: y,
        w: bb.w - 2 * x,
        h: bb.h - 2 * y
    };
}

I encountered some problems with the gamma-calculation, and modified it to take into account in which direction the original box is the longest.

-- Magnus Hoff

Answer 2

Trying not to break tradition putting the solution of the problem as a picture:)

---

Edit: Third equations is wrong. The correct one is:

3.w * cos(α) * X + w * sin(α) * Y - w * w * sin(α) * cos(α) - w * h = 0

To solve the system of linear equations you can use Cramer rule, or Gauss method.

Answer 3

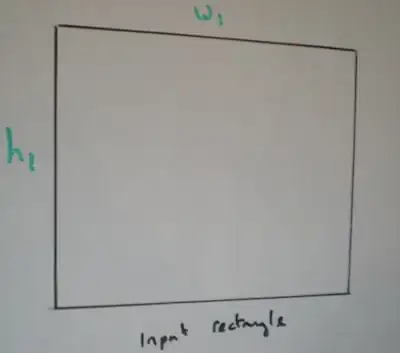
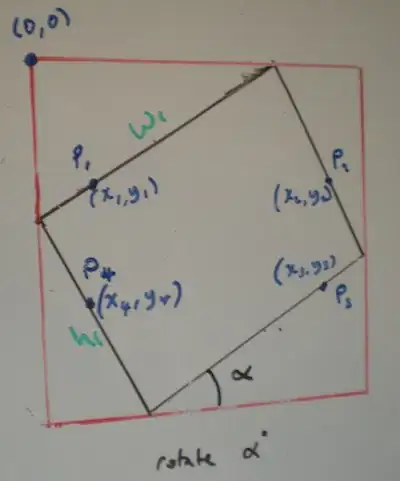
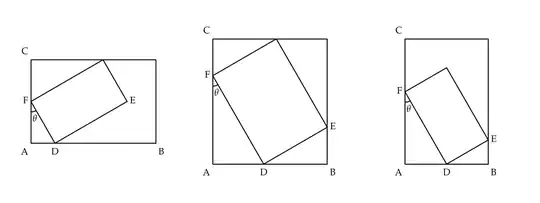
First, we take care of the trivial case where the angle is zero or a multiple of pi/2. Then the largest rectangle is the same as the original rectangle.

In general, the inner rectangle will have 3 points on the boundaries of the outer rectangle. If it does not, then it can be moved so that one vertex will be on the bottom, and one vertex will be on the left. You can then enlarge the inner rectangle until one of the two remaining vertices hits a boundary.

We call the sides of the outer rectangle R1 and R2. Without loss of generality, we can assume that R1 <= R2. If we call the sides of the inner rectangle H and W, then we have that

H cos a + W sin a <= R1
H sin a + W cos a <= R2

Since we have at least 3 points on the boundaries, at least one of these inequality must actually be an equality. Let's use the first one. It is easy to see that:

W = (R1 - H cos a) / sin a

and so the area is

A = H W = H (R1 - H cos a) / sin a

We can take the derivative wrt. H and require it to equal 0:

dA/dH = ((R1 - H cos a) - H cos a) / sin a

Solving for H and using the expression for W above, we find that:

H = R1 / (2 cos a)
W = R1 / (2 sin a)

Substituting this in the second inequality becomes, after some manipulation,

R1 (tan a + 1/tan a) / 2 <= R2

The factor on the left-hand side is always at least 1. If the inequality is satisfied, then we have the solution. If it isn't satisfied, then the solution is the one that satisfies both inequalities as equalities. In other words: it is the rectangle which touches all four sides of the outer rectangle. This is a linear system with 2 unknowns which is readily solved:

H = (R2 cos a - R1 sin a) / cos 2a
W = (R1 cos a - R2 sin a) / cos 2a

In terms of the original coordinates, we get:

x1 = x4 = W sin a cos a
y1 = y2 = R2 sin a - W sin^2 a 
x2 = x3 = x1 + H
y3 = y4 = y2 + W

Answer 4

@Andri is not working correctly for image where width > height as I tested. So, I fixed and optimized his code by such way (with only two trigonometric functions):

calculateLargestRect = function(angle, origWidth, origHeight) {
    var w0, h0;
    if (origWidth <= origHeight) {
        w0 = origWidth;
        h0 = origHeight;
    }
    else {
        w0 = origHeight;
        h0 = origWidth;
    }
    // Angle normalization in range [-PI..PI)
    var ang = angle - Math.floor((angle + Math.PI) / (2*Math.PI)) * 2*Math.PI; 
    ang = Math.abs(ang);      
    if (ang > Math.PI / 2)
        ang = Math.PI - ang;
    var sina = Math.sin(ang);
    var cosa = Math.cos(ang);
    var sinAcosA = sina * cosa;
    var w1 = w0 * cosa + h0 * sina;
    var h1 = w0 * sina + h0 * cosa;
    var c = h0 * sinAcosA / (2 * h0 * sinAcosA + w0);
    var x = w1 * c;
    var y = h1 * c;
    var w, h;
    if (origWidth <= origHeight) {
        w = w1 - 2 * x;
        h = h1 - 2 * y;
    }
    else {
        w = h1 - 2 * y;
        h = w1 - 2 * x;
    }
    return {
        w: w,
        h: h
    }
}

UPDATE

Also I decided to post the following function for proportional rectange calculating:

calculateLargestProportionalRect = function(angle, origWidth, origHeight) {
    var w0, h0;
    if (origWidth <= origHeight) {
        w0 = origWidth;
        h0 = origHeight;
    }
    else {
        w0 = origHeight;
        h0 = origWidth;
    }
    // Angle normalization in range [-PI..PI)
    var ang = angle - Math.floor((angle + Math.PI) / (2*Math.PI)) * 2*Math.PI; 
    ang = Math.abs(ang);      
    if (ang > Math.PI / 2)
        ang = Math.PI - ang;
    var c = w0 / (h0 * Math.sin(ang) + w0 * Math.cos(ang));
    var w, h;
    if (origWidth <= origHeight) {
        w = w0 * c;
        h = h0 * c;
    }
    else {
        w = h0 * c;
        h = w0 * c;
    }
    return {
        w: w,
        h: h
    }
}

Answer 5

Edit: My Mathematica answer below is wrong - I was solving a slightly different problem than what I think you are really asking.

To solve the problem you are really asking, I would use the following algorithm(s):

On the Maximum Empty Rectangle Problem

Using this algorithm, denote a finite amount of points that form the boundary of the rotated rectangle (perhaps a 100 or so, and make sure to include the corners) - these would be the set S decribed in the paper.

.

.

.

.

.

For posterity's sake I have left my original post below:

The inside rectangle with the largest area will always be the rectangle where the lower mid corner of the rectangle (the corner near the alpha on your diagram) is equal to half of the width of the outer rectangle.

I kind of cheated and used Mathematica to solve the algebra for me:

From this you can see that the maximum area of the inner rectangle is equal to 1/4 width^2 * cosecant of the angle times the secant of the angle.

Now I need to figure out what is the x value of the bottom corner for this optimal condition. Using the Solve function in mathematica on my area formula, I get the following:

Which shows that the x coordinate of the bottom corner equals half of the width.

Now just to make sure, I'll going to test our answer empirically. With the results below you can see that indeed the highest area of all of my tests (definately not exhaustive but you get the point) is when the bottom corner's x value = half of the outer rectangle's width.

Answer 6

Coproc solved this problem on another thread (https://stackoverflow.com/a/16778797) in a simple and efficient way. Also, he gave a very good explanation and python code there.

Below there is my Matlab implementation of his solution:

function [ CI, T ] = rotateAndCrop( I, ang )
%ROTATEANDCROP Rotate an image 'I' by 'ang' degrees, and crop its biggest
% inner rectangle.

[h,w,~] = size(I);
ang = deg2rad(ang);

% Affine rotation
R = [cos(ang) -sin(ang) 0; sin(ang) cos(ang) 0; 0 0 1];
T = affine2d(R);
B = imwarp(I,T);

% Largest rectangle
% solution from https://stackoverflow.com/a/16778797

wb = w >= h;
sl = w*wb + h*~wb;
ss = h*wb + w*~wb;

cosa = abs(cos(ang));
sina = abs(sin(ang));

if ss <= 2*sina*cosa*sl
    x = .5*min([w h]);
    wh = wb*[x/sina x/cosa] + ~wb*[x/cosa x/sina];
else
    cos2a = (cosa^2) - (sina^2);
    wh = [(w*cosa - h*sina)/cos2a (h*cosa - w*sina)/cos2a]; 
end

hw = flip(wh);

% Top-left corner
tl = round(max(size(B)/2 - hw/2,1));

% Bottom-right corner
br = tl + round(hw);

% Cropped image
CI = B(tl(1):br(1),tl(2):br(2),:);

Answer 7

sorry for not giving a derivation here, but I solved this problem in Mathematica a few days ago and came up with the following procedure, which non-Mathematica folks should be able to read. If in doubt, please consult http://reference.wolfram.com/mathematica/guide/Mathematica.html

The procedure below returns the width and height for a rectangle with maximum area that fits into another rectangle of width w and height h that has been rotated by alpha.

CropRotatedDimensionsForMaxArea[{w_, h_}, alpha_] := 
With[
  {phi = Abs@Mod[alpha, Pi, -Pi/2]},
  Which[
   w == h, {w,h} Csc[phi + Pi/4]/Sqrt[2],
   w > h, 
     If[ Cos[2 phi]^2 < 1 - (h/w)^2, 
       h/2 {Csc[phi], Sec[phi]}, 
       Sec[2 phi] {w Cos[phi] - h Sin[phi], h Cos[phi] - w Sin[phi]}],
   w < h, 
     If[ Cos[2 phi]^2 < 1 - (w/h)^2, 
       w/2 {Sec[phi], Csc[phi]}, 
       Sec[2 phi] {w Cos[phi] - h Sin[phi], h Cos[phi] - w Sin[phi]}]
  ]
]

Answer 8

Here is the easiest way to do this... :)

Step 1
//Before Rotation

int originalWidth = 640;
int originalHeight = 480;

Step 2
//After Rotation
int newWidth = 701;  //int newWidth = 654;  //int newWidth = 513;
int newHeight = 564; //int newHeight = 757; //int newHeight = 664;

Step 3
//Difference in height and width
int widthDiff ;
int heightDiff;
int ASPECT_RATIO = originalWidth/originalHeight; //Double check the Aspect Ratio

if (newHeight > newWidth) {

    int ratioDiff = newHeight - newWidth;
    if (newWidth < Constant.camWidth) {
        widthDiff = (int) Math.floor(newWidth / ASPECT_RATIO);
        heightDiff = (int) Math.floor((originalHeight - (newHeight - originalHeight)) / ASPECT_RATIO);
    }
    else {
        widthDiff = (int) Math.floor((originalWidth - (newWidth - originalWidth) - ratioDiff) / ASPECT_RATIO);
        heightDiff = originalHeight - (newHeight - originalHeight);
    }

} else {
    widthDiff = originalWidth - (originalWidth);
    heightDiff = originalHeight - (newHeight - originalHeight);
}

Step 4
//Calculation
int targetRectanleWidth = originalWidth - widthDiff;
int targetRectanleHeight = originalHeight - heightDiff;

Step 5
int centerPointX = newWidth/2;
int centerPointY = newHeight/2;

Step 6
int x1 = centerPointX - (targetRectanleWidth / 2); 
int y1 = centerPointY - (targetRectanleHeight / 2);
int x2 = centerPointX + (targetRectanleWidth / 2);
int y2 = centerPointY + (targetRectanleHeight / 2);

Step 7
x1 = (x1 < 0 ? 0 : x1);
y1 = (y1 < 0 ? 0 : y1);

Answer 9

This is just an illustration of Jeffrey Sax's solution above, for my future reference.

With reference to the diagram above, the solution is:

(I used the identity tan(t) + cot(t) = 2/sin(2t))