15

How to get arrows for the axes when using the command Plot in Mathematica?

Thanks for any helpful answers.

Sjoerd C. de Vries
  • 16,122
  • 3
  • 42
  • 94
user376089
  • 1,245
  • 3
  • 14
  • 18
  • 1
    By Simon, for example http://groups.google.com/group/comp.soft-sys.math.mathematica/browse_thread/thread/cec6c6757e321ec5 – Dr. belisarius Apr 30 '11 at 21:54
  • 1
    You might also be interested in the answers to [this](http://stackoverflow.com/questions/5074921/plotting-arrows-at-the-edges-of-a-curve) SO question (_Plotting Arrows at the End of a Curve_), also posted by Simon – 681234 Apr 30 '11 at 22:32

3 Answers3

19

For 2D plots such as generated by Plot the following works great:

Plot[Sin[x], {x, 0, 10}, AxesStyle -> Arrowheads[0.07]]

enter image description here

or with custom arrow heads:

h = Graphics[Line[{{-1, 1/2}, {0, 0}, {-1, -1/2}}]];
Plot[Sin[x], {x, 0, 10}, 
 AxesStyle -> Arrowheads[{{Automatic, Automatic, h}}]]

enter image description here

Sjoerd C. de Vries
  • 16,122
  • 3
  • 42
  • 94
7

Building on Sjoerd's answer,

a plot such as

enter image description here

may be obtained as follows (for example): 

       Plot[Sin[x], {x, -2\[Pi], 2 \[Pi]},

 AxesStyle-> { 

Directive[{Red,
Arrowheads[{{-0.06,0(*Xleft*),{Graphics[{
Polygon[
{{-1,0.5`},{0,0},{-1,-0.5`}}]}],0.98`}},
{0.03,.9(*Xright*),{Graphics[{
Polygon[
{{-1,0.5`},{0,0},{-1,-0.5`}}]}],0.98`}}}]}], 

Directive[{Blue,
Arrowheads[{{-0.05,0(*Ydown*),{Graphics[{
Polygon[
{{-1,0.5`},{0,0},{-1,-0.5`}}]}],0.98`}},{0.03,.8(*Yup*),{Graphics[{
Polygon[
{{-1,0.5`},{0,0},{-1,-0.5`}}]}],0.98`}}}]}
]}]

There are nice examples of arrowheads given in Drawings Tools and Graphics Inspector. There are probably much better ways of getting the info but I annotate a plot with an arrow that I like and then abstract (using a suggestion from Simon):

Cases["Paste-Graphic_Here", Arrowheads[___], Infinity]

To give another example:

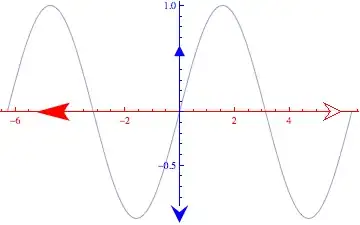
enter image description here

The code is as follows

Plot[Sin[x], {x, -2\[Pi],2 \[Pi]}, 
AxesStyle-> { Directive[{Red,

Arrowheads[{{-0.06,0.1(*Xleft*),
{Graphics[{arrowhead}]/.arrowhead-> arrowhead2,0.98`}},
{0.05,0.95(*Xright*),
{Graphics[{arrowhead}],0.98`}}}]/.arrowhead-> arrowhead4}], 

Directive[{Blue,
Arrowheads[{{-0.05,0(*Ydown*),
{Graphics[{arrowhead}]/.arrowhead-> arrowhead3,0.98`}},{0.03,.8(*Yup*),
{Graphics[{arrowhead}]/.arrowhead-> arrowhead1,0.98`}}}]}

]}]

where

arrowhead1=Polygon[{{-1,0.5`},{0,0},{-1,-0.5`}}];

arrowhead2=Polygon[{{-1.5833333333333333`,0.4166666666666667`},{-1.5410500000000003`,0.369283333333333`},{-1.448333333333333`,0.255583333333333`},{-1.3991000000000005`,0.18721666666666673`},{-1.3564666666666663`,0.11826666666666673`},{-1.3268499999999999`,0.05408333333333341`},{-1.3166666666666667`,0.`},{-1.3268499999999999`,-0.048950000000000195`},{-1.3564666666666663`,-0.11228333333333372`},{-1.3991000000000005`,-0.18353333333333333`},{-1.448333333333333`,-0.2562833333333335`},{-1.5410500000000003`,-0.38048333333333345`},{-1.5833333333333333`,-0.43333333333333335`},{0.`,0.`},{-1.5833333333333333`,0.4166666666666667`},{-1.5833333333333333`,0.4166666666666667`}}];

arrowhead3=Polygon[{{-1,0.5`},{0,0},{-1,-0.5`},{-0.6`,0},{-1,0.5`}}];

arrowhead4={{FaceForm[GrayLevel[1]],Polygon[{{-0.6`,0},{-1.`,0.5`},{0.`,0},{-1.`,-0.5`},{-0.6`,0}}],Line[{{-0.6`,0},{-1.`,0.5`},{0.`,0},{-1.`,-0.5`},{-0.6`,0}}]}};

arrowhead5=Polygon[{{-0.6582278481012658`,-0.43037974683544306`},{0.`,0.`},{0.`,0.`},{0.`,0.`},{0.`,0.`},{0.`,0.`},{-0.6455696202531646`,0.43037974683544306`},{-0.4810126582278481`,0.`},{-0.6582278481012658`,-0.43037974683544306`},{-0.6582278481012658`,-0.43037974683544306`}}];

A list of arrowheads 1 to 5:

enter image description here

Community
  • 1
  • 1
681234
  • 4,214
  • 2
  • 35
  • 42
5

Here you have a solution posted in https://math.stackexchange.com/

As the solution in the reference is for Plot3D, here I modified (but not improved) it for Plot[ ]: 

axes[x_, y_, f_, a_] := 
 Graphics[Join[{Arrowheads[a]}, 
   Arrow[{{0, 0}, #}] & /@ {{x, 0}, {0, y}}, 
   {Text[Style["x", FontSize -> Scaled[f]], {0.9*x, 0.1*y}], 
    Text[Style["y", FontSize -> Scaled[f]], {0.1 x, 0.95*y}]
   }]]

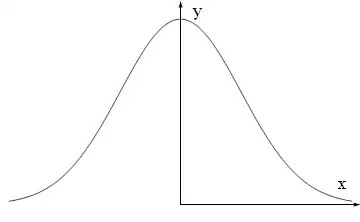
Show[Plot[Exp[-x^2], {x, -2, 2}, 
       Axes -> None, 
       PlotRange -> {{-2.1, 2.1}, {-.1, 1.1}}], 
     axes[2, 1, 0.05, 0.02]
]

enter image description here

Community
  • 1
  • 1
Dr. belisarius
  • 60,527
  • 15
  • 115
  • 190
  • 1
    What's wrong with them then? Actually, I'd say that the axes above are a bit unusual. In 2D plots you don't normally see curves in areas without axes. – Sjoerd C. de Vries Apr 30 '11 at 22:39
  • @Sjoerd: Yes, I know. I was almost finished formatting my answer and uploading images when I got a notification that you had just posted the exact same answer :( – abcd Apr 30 '11 at 23:17