I have a very simple method which finds the closest point on a line given a test point. Which is achieved by projecting vectorA on vectorB, such that:
Point testPoint
VectorA = testPoint - Origin VectorB
VectorC = (VectorA * VectorB / |VectorB|^2) VectorB
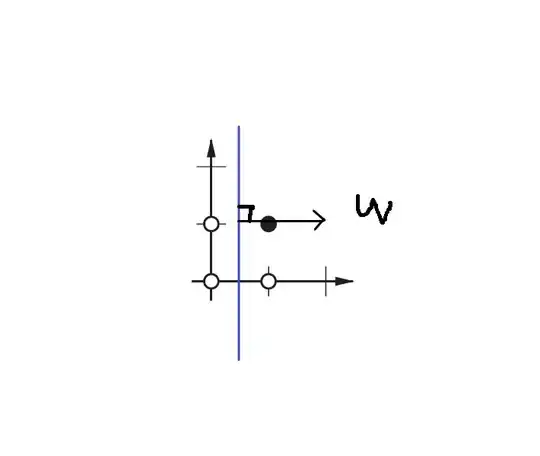
Like in the following image:
The Problem that I am having is that in some cases the Projected point is not on the line. How can I guarantee in my method such behavior?
/// <summary>
/// Returns the dot product of two vectors
/// This value equals vecA.Magnitude * vecB.Magnitude * cos(theta), where theta is the angle between both vectors.
/// </summary>
/// <param name="vecA"></param>
/// <param name="VecB"></param>
/// <returns></returns>
public static double DotProduct(Vec3 vecA, Vec3 VecB)
{
return vecA.X * VecB.X + vecA.Y * VecB.Y + vecA.Z * VecB.Z;
}
/// <summary>
/// Projection of vecA on to vecB
/// </summary>
/// <param name="vecA"></param>
/// <param name="vecB"></param>
/// <returns></returns>
public static Vec3 Project(Vec3 vecA, Vec3 vecB)
{
return DotProduct(vecA, vecB) / vecB.SqrMagnitude * vecB;
}
/// <summary>
/// Finds the closest point on a vector given a test point
/// </summary>
/// <param name="testPoint"></param>
/// <param name="startVertex"></param>
/// <param name="segment"></param>
/// <returns></returns>
public static Vec3 VectorClosestPoint(Vec3 testPoint, Vec3 startVertex,Vec3 segment)
{
Vec3 b = testPoint - startVertex;
Vec3 proj = Project(b, segment);
Vec3 onCurve = startVertex + proj;
return onCurve;
}
Any hints would be very helpful