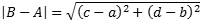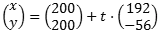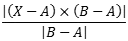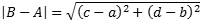There are correct answers already, but I think it might be more generally useful to have a formula that gives the distance of any point from a specified line. Then you can just check if this is zero, or within whatever tolerance you choose. The following should work regardless of special cases like vertical lines (infinite gradient).
The distance of point X from the line AB is
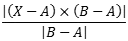
where A, B and X are the 3D position vectors of the three points (just set z = 0 if you are only working in 2D) and x is the vector product. That comes to
where A = (a,b), B = (c,d) and X = (x,y). Then to check that the point is actually within the line segment and not elsewhere on the infinite line, you can use the scalar products: the distance of X along the line from A to B is
i.e.
and this should lie between 0 and