5

I have a lot of polygons, and after I do a union of all these polygons, I get a new, big polygon. The union algorithm is a black box and using third-party-library process, which I couldn't control, and neither can I hope to extract any information out kind of progress.

Is there efficient way for me to know, for every edge of that big gigantic unionized polygon, which of it is belonging to which edge of the smaller polygon?

A brute force way to solve this problem is to compare every edge of the unionized polygon with each of the smaller polygons, but this is going to be very inefficient. Any other more efficient techniques?

My hunch tells me that sweep line algorithm may help here, although I have absolutely no idea how to do it.

Edit: The small npolygons can overlap, so the union polygon can contain points that are located at the edges of the small polygons, but these points may not be the vertexes of the original polygons.

A screenshot of this is shown below:

Graviton
  • 81,782
  • 146
  • 424
  • 602
  • How do you "unionize" your polygons? My guess is that when you do that union, you can store somewhere the association between the small polygon edges, and their counterpart in the big one. – B. Decoster Jun 15 '11 at 08:08
  • @Fezvez, the union is something which I don't control. See the updated question. – Graviton Jun 15 '11 at 08:10

3 Answers3

3

Here is one solution.

Take each original edge. They can be (over)specified by 3 things:

  1. A vector indicating direction
  2. Starting point
  3. Ending point

The first step is to normalize the vectors (eg multiply by a scalar so that the larger in absolute value of x and y is 1). Then store all of your edges into a hash whose keys are those vectors, and whose values are an array of edges with that vector. (If you have a lot of edges, you might consider using an interval tree for the edges.)

Now given an edge on the combined polygon, you can figure out its vector, look in your hash, and you'll generally have only a small number of edges in the original polygon with that exact vector, so it isn't too hard to go through them and figure out which ones overlapped.

Note that while this solution will let you fairly efficiently find cases where the edge runs along the boundary, it will miss cases where a polygon just touches the boundary of the combined polygon at one corner. Hopefully that doesn't matter for you.

btilly
  • 43,296
  • 3
  • 59
  • 88
  • what do you mean by ` miss cases where a polygon just touches the boundary of the combined polygon at one corner`? From what I can see it won't, because all the edges on the combined polygon will somehow, located at the edges of the original polygons, no? – Graviton Jun 16 '11 at 02:52
  • @Graviton, take a pentagon, slice it into 4 triangles that meet at a corner. All 4 touch that corner, but this algorithm will only notice that 2 of them touch that spot. – btilly Jun 16 '11 at 04:29
  • I can imagine the pentagon you mention, but I run your algorithm on that case and yet I can still get back the answer I want; what is the problem here? – Graviton Jun 16 '11 at 04:41
  • @Graviton: It depends on what you want. You'll miss some one point intersections. But I suspect that you don't care about them. If you don't, then the solution does what you want. – btilly Jun 16 '11 at 06:50
2

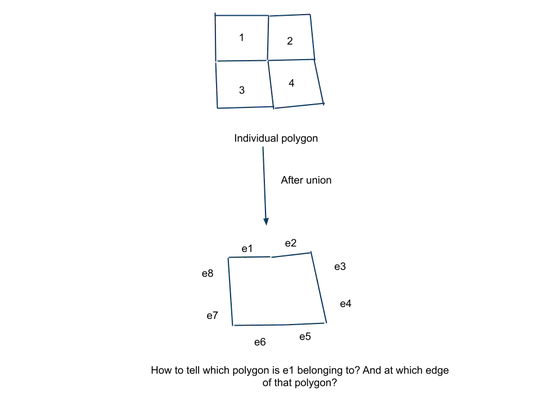
Since the naive approach doesn't work because of new edges and vertexes appearing in the union (see the old answer and comments), we will need to employ a more complicated data structure.

The idea is to identify an edge in the input set that contains the edge of the output set. By "contains" I mean both vertexes of the edge from the output set needs to be on the edge from the input set. So, we need to search the input edge set for one that contains a line segment that passes through both vertexes of the edge we are considering.

A simple way to filter out a large number of the edge set for the search is to use bounding boxes: if the vertex we are checking doesn't lie inside the bounding box formed by the two vertexes of an edge, then we can rule it out. The main algorithm, then is:

INPUT: An edge from the output polygon, E1, with V1 and V2 as the end points.

OUTPUT: An edge from the input polygons where both V1 and V2 are on the edge.

  • Get the set of edges from input set whose bounding boxes contain both V1 and V2 (or in other words, the bounding box formed by V1, V2)
  • Brute force search for the edge which both V1 and V2 lie on.

Second step is obvious. There are a few places to look at for the first one. A K-D tree (the volumetric object) looks like it would solve the problem. Or maybe an R-tree. Also check stackoverflow for similar questions. Unfortunately, I am not very well-versed in the spatial algorithms to suggest a suitable one.

OLD ANSWER:

I don't think you need any fancy data structures to handle the case. I am assuming that the coordinates of the vertexes in the union are identical to the ones in your original set. So you can do something like: create a list of vertexes for your input data, where each vertex records the polygon(s) it belongs to. Make these easily searchable: a naive approach would be to sort them by one coordinate first, and then the other. You can find any vertex in O(log n) that way.

Now, for any given edge of the union polygon, search for the first vertex of the edge, then search the other. Take the set intersection of the polygons they belong to, and you get the original polygon. To speed up the searching for second vertex, you can also add a list of connected vertexes to the original list, so that you don't do a full search again.

A final optimization is pre-calculation: just run the above algorithm, and record the results for each edge, then get rid of all the vertex and edge tables. If you don't need a pre-calculated table, you can filter out the original vertex set for vertexes that don't appear in the union.

Community
  • 1
  • 1
vhallac
  • 13,301
  • 3
  • 25
  • 36
  • Not too sure whether this works, as when I union all of the polygon, new vertexes-- the ones that don't belong to the original polygons-- can appear in the union polygon. – Graviton Jun 15 '11 at 08:35
  • You may want to clarify the question, then. For the case of new vertexes appearing, the simple solution above will not be enough. You also need to describe the characteristics of these new vertexes: how do you determine if they belong to a polygon of the original? – vhallac Jun 15 '11 at 08:37
  • what I mean is, imagine if two polygons overlap, so the union of the two polygons will create points that are not on the vertex of the original two polygons, but those points will locate at the edges of the polygons. This is what I mean by new vertex appearing – Graviton Jun 15 '11 at 09:00
  • @Graviton Gotcha. For that case, you will need a better data structure to determine edges that may contain this new vertex quickly. A K-D tree seems to solve the problem. I'll update the answer if I can find something. – vhallac Jun 15 '11 at 09:14
0

You can make BSP, or more concrete quadtree, with polygons edges. For each edge remember in which polygon(s) it is used.

For each edge in output polygon perform tree search and check for edge overlapping only with edges in quadtree leaf node(s).

Lets there be n edges in original polygons, and m edges in output polygon. To create tree O(n log n) is needed and to search overlapping of edges O(m log n) is needed. Overall O((m+n)*log n).

Note: if a whole edge is used in 2 initial polygons than it is not in output polygon boundary. With this you can remove duplicated edges from quadtree. Not necessary.

It is possible to make it other way. Create quadtree of output polygon edges, and search for each edge of initial polygons. Running time is O((m+n)*log m), which is faster. But with upper approach you can extract more informations from input polygons if you will need it in the future.

Ante
  • 5,350
  • 6
  • 23
  • 46