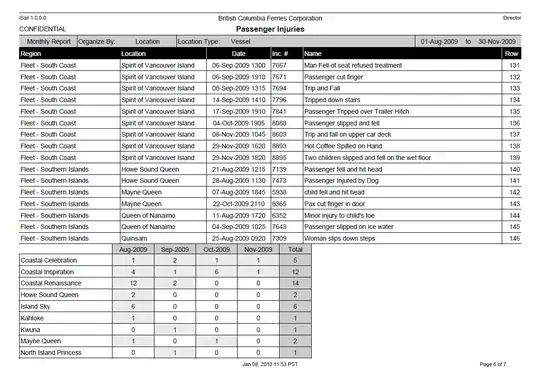
I have a problem, where I have a non-directed, non weighted graph, with a starting node s, a sink node t, and a special node w.
Now, I need to find a simple path from s to t, that goes from s to t, with the one constraint that the path should go through w. Just reapeating no vertices
I've seen variations of this question here, where people are using a weighted graph, and are trying to find the shortest path. This makes the problem into a variation of travelling salesman, which would make it np-hard.
but i my case, can I solve this simple problem in polynomial time? since I have to few constraints?