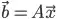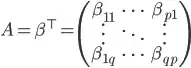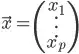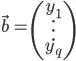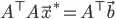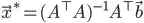This SO answer describes how to find the point closest to multiple lines in n-dimensional space using the least-squares method. Is there any existing implementation of this, but for the point closest to multiple m-flats in n-dimensional space?
My use case is that I used Multivariate Linear Regression to determine a relationship between an independent variable vector x and a dependent variable vector y, and now I'd like to find x that would make the stochastic process output values as closes as possible to experimental data y_exp. Since running MvLR yields a set of n-dimensional equations like so...
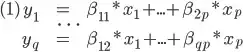
...and I have experimental values for y_1, ... y_q, each of these equations represents the intersection between two (n-1)-flat in n-dimensional space (one described by equation (1), and the other by y_1 = y_exp_1), which should yield an (n-2)-flat.
Is there an existing implementation to find a good set of x_1, ... x_p that gets me closest to these (n-2)-flats?