Solving simple ODE system within tkinter GUI

Question

I have a simple ODE system for an SIR disease model that works fine and produces a graphic plot. However I am trying to use tkinter to create a simple pop up box that takes parameter values instead of having to put them in through the script.

here is the original code.

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

#three compartments, Susceptible S, infected I, recovered R
#dS/dt, dI/dt, dR/dt
#susceptible sees birth rate coming in, deaths leaving and force of infection leaving
#infected sees FOI coming in, deaths leaving and recovery rates
#recovered sees recovery rate coming in, deaths leaving
#beta is tranmission coefficient, FOI is beta * (I/N) where N is total pop
#initially consider a model not accounting for births and deaths




# Total population, N.
N = 1000
# Initial number of infected and recovered individuals, I0 and R0.
I0, R0 = 1, 0
# Everyone else, S0, is susceptible to infection initially.
S0 = N - I0 - R0
# Contact rate, beta, and mean recovery rate, gamma, (in 1/days).
beta, gamma = 2/7, 1/7
# A grid of time points (in days)
t = np.linspace(0, 160, 160)

# The SIR model differential equations.
def deriv(y, t, N, beta, gamma):
    S, I, R = y
    dS = ((-beta * S * I) / N)
    dI = ((beta * S * I) / N) - (gamma * I)
    dR = (gamma * I)
    return dS, dI, dR

# Initial conditions are S0, I0, R0
# Integrate the SIR equations over the time grid, t.
solve = odeint(deriv, (S0, I0, R0), t, args=(N, beta, gamma))
S, I, R = solve.T

# Plot the data on three separate curves for S(t), I(t) and R(t)
fig = plt.figure(facecolor='w')
ax = fig.add_subplot(111, facecolor='#dddddd', axisbelow=True)
ax.plot(t, S/1000, 'b', alpha=1, lw=2, label='Susceptible')
ax.plot(t, I/1000, 'r', alpha=1, lw=2, label='Infected')
ax.plot(t, R/1000, 'black', alpha=1, lw=2, label='Recovered')
ax.set_xlabel('Time in days')
ax.set_ylabel('Number (1000s)')
ax.set_ylim(0,1.1)
#ax.yaxis.set_tick_params(length=0)
#ax.xaxis.set_tick_params(length=0)
ax.grid(b=True, which='major', c='w', lw=2, ls='-')
legend = ax.legend()
legend.get_frame().set_alpha(0.5)
#for spine in ('top', 'right', 'bottom', 'left'):
#    ax.spines[spine].set_visible(False)
plt.show()

Now here is the one with some GUI

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import tkinter as tk
from tkinter import IntVar

###############################################################################


def mainwindow():
    mainwindow = tk.Tk()
    mainwindow.geometry('350x350')
    
    tk.Label(mainwindow, text="enter parameters below").grid(row=1)
    
    getN = IntVar()
    geti0 = IntVar()
    getr0 = IntVar()
    getbeta = IntVar()
    getgamma = IntVar()

    
    tk.Label(mainwindow, text="N").grid(row=2)
    tk.Label(mainwindow, text="i0").grid(row=3)
    tk.Label(mainwindow, text="r0").grid(row=4)
    tk.Label(mainwindow, text="beta").grid(row=5)
    tk.Label(mainwindow, text="gamma").grid(row=6)
    
    e1 = tk.Entry(mainwindow,textvariable = getN).grid(row=2, column=1)
    e2 = tk.Entry(mainwindow,textvariable = geti0).grid(row=3, column=1)
    e3 = tk.Entry(mainwindow,textvariable = getr0).grid(row=4, column=1)
    e4 = tk.Entry(mainwindow,textvariable = getbeta).grid(row=5, column=1)
    e5 = tk.Entry(mainwindow,textvariable = getgamma).grid(row=6, column=1)
    
    solve = tk.Button(mainwindow, text='solve!', command=lambda: [values()]).grid(row=7, column=1, sticky=tk.W, pady=4)
    
    
    
    def values():
        
        readN = getN.get()
        readi0 = geti0.get()
        readr0 = getr0.get()
        readbeta = getbeta.get()
        readgamma = getgamma.get()
        
        intN = int(readN)
        inti0 = int(readi0)
        intr0 = int(readr0)
        intbeta = int(readbeta)
        intgamma = int(readgamma)
        
        
        # Total population, N.
        N = readN
        # Initial number of infected and recovered individuals, I0 and R0.
        I0, R0 = readi0, readr0
        # Everyone else, S0, is susceptible to infection initially.
        S0 = N - I0 - R0
        # Contact rate, beta, and mean recovery rate, gamma, (in 1/days).
        beta, gamma = readbeta, readgamma
        # A grid of time points (in days)
        t = np.linspace(0, 160, 160)

        # The SIR model differential equations.
        def deriv(y, t, N, beta, gamma):
            S, I, R = y
            dS = ((-beta * S * I) / N)
            dI = ((beta * S * I) / N) - (gamma * I)
            dR = (gamma * I)
            return dS, dI, dR
        
        # Initial conditions are S0, I0, R0
        # Integrate the SIR equations over the time grid, t.
        solve = odeint(deriv, (S0, I0, R0), t, args=(N, beta, gamma))
        S, I, R = solve.T
        
        # Plot the data on three separate curves for S(t), I(t) and R(t)
        fig = plt.figure(facecolor='w')
        ax = fig.add_subplot(111, facecolor='#dddddd', axisbelow=True)
        ax.plot(t, S/1000, 'b', alpha=0.5, lw=2, label='Susceptible')
        ax.plot(t, I/1000, 'r', alpha=0.5, lw=2, label='Infected')
        ax.plot(t, R/1000, 'g', alpha=0.5, lw=2, label='Recovered with immunity')
        ax.set_xlabel('Time /days')
        ax.set_ylabel('Number (1000s)')
        ax.set_ylim(0,1.2)
        ax.yaxis.set_tick_params(length=0)
        ax.xaxis.set_tick_params(length=0)
        ax.grid(b=True, which='major', c='w', lw=2, ls='-')
        legend = ax.legend()
        legend.get_frame().set_alpha(0.5)
        for spine in ('top', 'right', 'bottom', 'left'):
            ax.spines[spine].set_visible(False)
        plt.show()



    mainwindow.mainloop()
    
mainwindow()

The first gives the expected plot:

, however with the GUI it gives this:

Where has my code gone wrong? The code to solve the system hasnt changed, ive just set it so that the parameters take the values I enter in the pop up box. Has something gone wrong in the lambda function?

pippo1980 · Accepted Answer · 2021-09-10T21:26:16.723

hi tried your code with beta and gamma as 2/7 , 1/7 wasnt able to make it work.

using:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import tkinter as tk
from tkinter import IntVar,StringVar,DoubleVar

###############################################################################


def mainwindow():
    mainwindow = tk.Tk()
    mainwindow.geometry('350x350')
    
    tk.Label(mainwindow, text="enter parameters below").grid(row=1)
    
    getN = IntVar()
    geti0 = IntVar()
    getr0 = IntVar()
    # getbeta = StringVar()
    # getgamma = StringVar()
    
    getbeta = DoubleVar()
    getgamma = DoubleVar()

    
    tk.Label(mainwindow, text="N").grid(row=2)
    tk.Label(mainwindow, text="i0").grid(row=3)
    tk.Label(mainwindow, text="r0").grid(row=4)
    tk.Label(mainwindow, text="beta").grid(row=5)
    tk.Label(mainwindow, text="gamma").grid(row=6)
    
    e1 = tk.Entry(mainwindow,textvariable = getN).grid(row=2, column=1)
    e2 = tk.Entry(mainwindow,textvariable = geti0).grid(row=3, column=1)
    e3 = tk.Entry(mainwindow,textvariable = getr0).grid(row=4, column=1)
    e4 = tk.Entry(mainwindow,textvariable = getbeta).grid(row=5, column=1)
    e5 = tk.Entry(mainwindow,textvariable = getgamma).grid(row=6, column=1)
    
    solve = tk.Button(mainwindow, text='solve!', command=lambda: [values()]).grid(row=7, column=1, sticky=tk.W, pady=4)
    
    
    
    def values():
        
        readN = getN.get()
        readi0 = geti0.get()
        readr0 = getr0.get()
        # readbeta = float(getbeta.get())
        # readgamma = float(getgamma.get())
        readbeta = (getbeta.get())
        readgamma =(getgamma.get())
        
        print('ppppppppppppp', readbeta,readgamma)
        
        intN = int(readN)
        inti0 = int(readi0)
        intr0 = int(readr0)
        intbeta = float(readbeta)
        intgamma = float(readgamma)
        
        
        # Total population, N.
        N = readN
        # Initial number of infected and recovered individuals, I0 and R0.
        I0, R0 = readi0, readr0
        # Everyone else, S0, is susceptible to infection initially.
        S0 = N - I0 - R0
        # Contact rate, beta, and mean recovery rate, gamma, (in 1/days).
        beta, gamma = readbeta, readgamma
        # A grid of time points (in days)
        t = np.linspace(0, 160, 160)

        # The SIR model differential equations.
        def deriv(y, t, N, beta, gamma):
            S, I, R = y
            dS = ((-beta * S * I) / N)
            dI = ((beta * S * I) / N) - (gamma * I)
            dR = (gamma * I)
            return dS, dI, dR
        
        # Initial conditions are S0, I0, R0
        # Integrate the SIR equations over the time grid, t.
        solve = odeint(deriv, (S0, I0, R0), t, args=(N, beta, gamma))
        S, I, R = solve.T
        
        # Plot the data on three separate curves for S(t), I(t) and R(t)
        fig = plt.figure(facecolor='w')
        ax = fig.add_subplot(111, facecolor='#dddddd', axisbelow=True)
        ax.plot(t, S/1000, 'b', alpha=0.5, lw=2, label='Susceptible')
        ax.plot(t, I/1000, 'r', alpha=0.5, lw=2, label='Infected')
        ax.plot(t, R/1000, 'g', alpha=0.5, lw=2, label='Recovered with immunity')
        ax.set_xlabel('Time /days')
        ax.set_ylabel('Number (1000s)')
        ax.set_ylim(0,1.2)
        ax.yaxis.set_tick_params(length=0)
        ax.xaxis.set_tick_params(length=0)
        ax.grid(b=True, which='major', c='w', lw=2, ls='-')
        legend = ax.legend()
        legend.get_frame().set_alpha(0.5)
        for spine in ('top', 'right', 'bottom', 'left'):
            ax.spines[spine].set_visible(False)
        plt.show()



    mainwindow.mainloop()
    
mainwindow()

and 0.28 , 0.14 as beta and gamma I get:

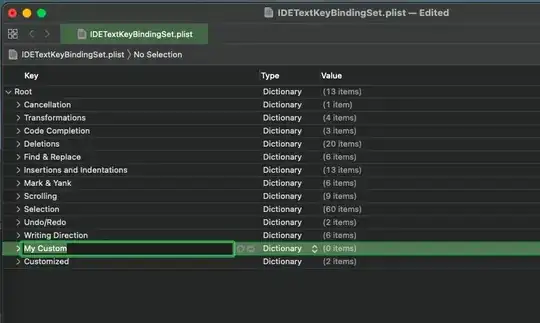
Hope somebody that knows how to use fraction as input will show up,

I tried using getbeta = StringVar() and getgamma = StringVar()

and readbeta = float(getbeta.get()) and readgamma =float(getgamma.get())

or intbeta = float(readbeta) and intgamma = float(readgamma)

but got ValueError: could not convert string to float: '2/7'

for readbeta = float(getbeta.get())

came accross use of eval to allow input of '2/7' and '1/7' as beta and gamma,see How can I get the data from Entry in tkinter that can be used as function?

here the code updated:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import tkinter as tk
from tkinter import IntVar,StringVar,DoubleVar

###############################################################################


def mainwindow():
    mainwindow = tk.Tk()
    mainwindow.geometry('350x350')
    
    tk.Label(mainwindow, text="enter parameters below").grid(row=1)
    
    getN = IntVar()
    geti0 = IntVar()
    getr0 = IntVar()
    getbeta = StringVar()
    getgamma = StringVar()
    
    # getbeta = DoubleVar()
    # getgamma = DoubleVar()

    
    tk.Label(mainwindow, text="N").grid(row=2)
    tk.Label(mainwindow, text="i0").grid(row=3)
    tk.Label(mainwindow, text="r0").grid(row=4)
    tk.Label(mainwindow, text="beta").grid(row=5)
    tk.Label(mainwindow, text="gamma").grid(row=6)
    
    e1 = tk.Entry(mainwindow,textvariable = getN).grid(row=2, column=1)
    e2 = tk.Entry(mainwindow,textvariable = geti0).grid(row=3, column=1)
    e3 = tk.Entry(mainwindow,textvariable = getr0).grid(row=4, column=1)
    e4 = tk.Entry(mainwindow,textvariable = getbeta).grid(row=5, column=1)
    e5 = tk.Entry(mainwindow,textvariable = getgamma).grid(row=6, column=1)
    
    solve = tk.Button(mainwindow, text='solve!', command=lambda: [values()]).grid(row=7, column=1, sticky=tk.W, pady=4)
    
    
    
    def values():
        
        readN = getN.get()
        readi0 = geti0.get()
        readr0 = getr0.get()
        # readbeta = float(getbeta.get())
        # readgamma = float(getgamma.get())  
        readbeta = eval(getbeta.get(),{"builtins": {}})
        readgamma = eval(getgamma.get(), {"builtins": {}})
        
        print('ppppppppppppp', readbeta,readgamma)
        
        intN = int(readN)
        inti0 = int(readi0)
        intr0 = int(readr0)
        intbeta = float(readbeta)
        intgamma = float(readgamma)
        
        
        # Total population, N.
        N = readN
        # Initial number of infected and recovered individuals, I0 and R0.
        I0, R0 = readi0, readr0
        # Everyone else, S0, is susceptible to infection initially.
        S0 = N - I0 - R0
        # Contact rate, beta, and mean recovery rate, gamma, (in 1/days).
        beta, gamma = readbeta, readgamma
        # A grid of time points (in days)
        t = np.linspace(0, 160, 160)

        # The SIR model differential equations.
        def deriv(y, t, N, beta, gamma):
            S, I, R = y
            dS = ((-beta * S * I) / N)
            dI = ((beta * S * I) / N) - (gamma * I)
            dR = (gamma * I)
            return dS, dI, dR
        
        # Initial conditions are S0, I0, R0
        # Integrate the SIR equations over the time grid, t.
        solve = odeint(deriv, (S0, I0, R0), t, args=(N, beta, gamma))
        S, I, R = solve.T
        
        # Plot the data on three separate curves for S(t), I(t) and R(t)
        fig = plt.figure(facecolor='w')
        ax = fig.add_subplot(111, facecolor='#dddddd', axisbelow=True)
        ax.plot(t, S/1000, 'b', alpha=0.5, lw=2, label='Susceptible')
        ax.plot(t, I/1000, 'r', alpha=0.5, lw=2, label='Infected')
        ax.plot(t, R/1000, 'g', alpha=0.5, lw=2, label='Recovered with immunity')
        ax.set_xlabel('Time /days')
        ax.set_ylabel('Number (1000s)')
        ax.set_ylim(0,1.2)
        ax.yaxis.set_tick_params(length=0)
        ax.xaxis.set_tick_params(length=0)
        ax.grid(b=True, which='major', c='w', lw=2, ls='-')
        legend = ax.legend()
        legend.get_frame().set_alpha(0.5)
        for spine in ('top', 'right', 'bottom', 'left'):
            ax.spines[spine].set_visible(False)
        plt.show()



    mainwindow.mainloop()
    
mainwindow()

it uses getbeta = StringVar() and getgamma = StringVar() and then readbeta = eval(getbeta.get(),{"builtins": {}}) and readgamma = eval(getgamma.get(), {"builtins": {}})

I read somewhere that use of eval is not safe in python so if anybody as a better solution please share it with us

At the end managed to validate input before sending it to eval function so code should be safe (or not ?? please help here) ; here the new code:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import tkinter as tk
from tkinter import IntVar,StringVar,DoubleVar

###############################################################################
def callback_int(input):
      
    if input.isdigit():
        print(input)
        return True
                          
    elif input == "":
        print(input)
        return True
  
    else:
        print(input)
        return False

def callback_str(input, typez=None):
    
    if all([s.isdigit() or s =='/' for s in input]) and input.count('/') <= 1:
        print([s.isdigit() or s =='/' for s in input])
        # print(input)
        return True
                          
    elif all([s.isdigit() or s =='.' for s in input]) and input.count('.') <= 1:
        print([s.isdigit() or s =='.' for s in input])
        # print(input)
        return True

    else:
        print('no valid input : ',input)
        return False

def mainwindow():

    mainwindow = tk.Tk()
    mainwindow.geometry('350x350')
    
    tk.Label(mainwindow, text="enter parameters below").grid(row=1)
    
    getN = IntVar()
    geti0 = IntVar()
    getr0 = IntVar()
    getbeta = StringVar(mainwindow, value='0')
    getgamma = StringVar(mainwindow, value='0')
    
    # getbeta = DoubleVar()
    # getgamma = DoubleVar()

    
    tk.Label(mainwindow, text="N").grid(row=2)
    tk.Label(mainwindow, text="i0").grid(row=3)
    tk.Label(mainwindow, text="r0").grid(row=4)
    tk.Label(mainwindow, text="beta").grid(row=5)
    tk.Label(mainwindow, text="gamma").grid(row=6)
    
    e1 = tk.Entry(mainwindow,textvariable = getN)
    e1.grid(row=2, column=1)
    e2 = tk.Entry(mainwindow,textvariable = geti0)
    e2.grid(row=3, column=1)
    e3 = tk.Entry(mainwindow,textvariable = getr0)
    e3.grid(row=4, column=1)
    e4 = tk.Entry(mainwindow,textvariable = getbeta)
    e4.grid(row=5, column=1)
    e5 = tk.Entry(mainwindow,textvariable = getgamma)
    e5.grid(row=6, column=1)
    
    reg_int = mainwindow.register(callback_int)
    reg_str = mainwindow.register(callback_str)
    
    print(type(e4))
    
    e1.config(validate ="key", validatecommand =(reg_int, '%P'))
    e2.config(validate ="key", validatecommand =(reg_int, '%P'))
    e3.config(validate ="key", validatecommand =(reg_int, '%P'))
    e4.config(validate ="key", validatecommand =(reg_str, '%P'))
    e5.config(validate ="key", validatecommand =(reg_str, '%P'))
    
    solve = tk.Button(mainwindow, text='solve!', command=lambda: [values()]).grid(row=7, column=1, sticky=tk.W, pady=4)
    
    
    
    def values():
        
        readN = getN.get()
        readi0 = geti0.get()
        readr0 = getr0.get()
        # readbeta = float(getbeta.get())
        # readgamma = float(getgamma.get())  
        readbeta = eval(getbeta.get(),{"builtins": {}})
        readgamma = eval(getgamma.get(), {"builtins": {}})
        
        print('ppppppppppppp', readbeta,readgamma)
        
        intN = int(readN)
        inti0 = int(readi0)
        intr0 = int(readr0)
        intbeta = float(readbeta)
        intgamma = float(readgamma)
        
        
        # Total population, N.
        N = readN
        # Initial number of infected and recovered individuals, I0 and R0.
        I0, R0 = readi0, readr0
        # Everyone else, S0, is susceptible to infection initially.
        S0 = N - I0 - R0
        # Contact rate, beta, and mean recovery rate, gamma, (in 1/days).
        beta, gamma = readbeta, readgamma
        # A grid of time points (in days)
        t = np.linspace(0, 160, 160)

        # The SIR model differential equations.
        def deriv(y, t, N, beta, gamma):
            S, I, R = y
            dS = ((-beta * S * I) / N)
            dI = ((beta * S * I) / N) - (gamma * I)
            dR = (gamma * I)
            return dS, dI, dR
        
        # Initial conditions are S0, I0, R0
        # Integrate the SIR equations over the time grid, t.
        solve = odeint(deriv, (S0, I0, R0), t, args=(N, beta, gamma))
        S, I, R = solve.T
        
        # Plot the data on three separate curves for S(t), I(t) and R(t)
        fig = plt.figure(facecolor='w')
        ax = fig.add_subplot(111, facecolor='#dddddd', axisbelow=True)
        ax.plot(t, S/1000, 'b', alpha=0.5, lw=2, label='Susceptible')
        ax.plot(t, I/1000, 'r', alpha=0.5, lw=2, label='Infected')
        ax.plot(t, R/1000, 'g', alpha=0.5, lw=2, label='Recovered with immunity')
        ax.set_xlabel('Time /days')
        ax.set_ylabel('Number (1000s)')
        ax.set_ylim(0,1.2)
        ax.yaxis.set_tick_params(length=0)
        ax.xaxis.set_tick_params(length=0)
        ax.grid(b=True, which='major', c='w', lw=2, ls='-')
        legend = ax.legend()
        legend.get_frame().set_alpha(0.5)
        for spine in ('top', 'right', 'bottom', 'left'):
            ax.spines[spine].set_visible(False)
        plt.show()

    
    mainwindow.mainloop()
    
mainwindow()

that allows for beta and gamma to insert float (i.e 0.28) or fractions (i.e. 2/7) as input into Entry widgets box

starting to enjoy Tkinter, here another improved version with RadioButtons controlling type of input allowed:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import tkinter as tk
from tkinter import IntVar,StringVar,DoubleVar

###############################################################################



def mainwindow():

    def switch():
        print(varb.get(), '    ')  #,varbR)
        # print(varbR)
        getbeta.set('0')
        getgamma.set('0')
        return
    
    def callback(input,typez=None, varb=None):
    
        value = mainwindow.getvar(varb)
        print(value)
        # varb.get()=varb.get()
        # uu = varb.get()
        # print(varb, uu)
        # print(varb.get())
        
        if typez == "int":
            if input.isdigit():
                # print(input)
                return True
                                
            elif input == "":
                # print(input)
                return True
        
            else:
                print(input, 'not allowed !!!!')
                return False
    
        if typez == "str":
            if value =='frc':
                if len(input) >=1  and input[0] == '/':
                    return False
                
                if all([s.isdigit() or s =='/' for s in input]) and input.count('/') <= 1:
                    # print([s.isdigit() or s =='/' for s in input])
                    # print(input)
                    return True
                else:
                    print('no valid input : ',input)
                    return False
            
            elif value =='flt':                   
                if all([s.isdigit() or s =='.' for s in input]) and input.count('.') <= 1:
                    # print([s.isdigit() or s =='.' for s in input])
                    # print(input)
                    return True
    
                else:
                    print('no valid input : ',input)
                    return False
            else:
                return False
    
    mainwindow = tk.Tk()
    mainwindow.geometry('550x350')
    
    tk.Label(mainwindow, text="enter parameters below").grid(row=1)
    
    getN = IntVar()
    geti0 = IntVar()
    getr0 = IntVar()
    getbeta = StringVar(mainwindow, value='0')
    getgamma = StringVar(mainwindow, value='0')
    
    # getbeta = DoubleVar()
    # getgamma = DoubleVar()

    
    tk.Label(mainwindow, text="N").grid(row=2)
    tk.Label(mainwindow, text="i0").grid(row=3)
    tk.Label(mainwindow, text="r0").grid(row=4)
    tk.Label(mainwindow, text="beta").grid(row=5)
    tk.Label(mainwindow, text="gamma").grid(row=6)
    
    e1 = tk.Entry(mainwindow,textvariable = getN)
    e1.grid(row=2, column=1)
    e2 = tk.Entry(mainwindow,textvariable = geti0)
    e2.grid(row=3, column=1)
    e3 = tk.Entry(mainwindow,textvariable = getr0)
    e3.grid(row=4, column=1)
    e4 = tk.Entry(mainwindow,textvariable = getbeta)
    e4.grid(row=5, column=1)
    e5 = tk.Entry(mainwindow,textvariable = getgamma)
    e5.grid(row=6, column=1)
    
    
    varb = StringVar(mainwindow, value='flt')
    # varbR=varb.get()
    
    
    rb1 = tk.Radiobutton(mainwindow, borderwidth=8,height=1, text='float   ' ,
                         variable = varb, value='flt', command=switch, justify="left")
    rb1.grid(row=5,column =2, rowspan=1, sticky="w")
    
    rb2 = tk.Radiobutton(mainwindow, borderwidth=8,height=1, text='fraction' ,
                         variable = varb, value='frc', command=switch ,justify="left")
    rb2.grid(row=6,column =2, rowspan=1, sticky="w")
    
    rb1.deselect()  # finche non attivo radiobutton non prende parametri
    
    
    
    
    reg = mainwindow.register(callback) 
    
    
    
    # e1.config(validate ="key", validatecommand =(reg, '%P', 'int',varbR))
    # e2.config(validate ="key", validatecommand =(reg, '%P', 'int',varbR))
    # e3.config(validate ="key", validatecommand =(reg, '%P', 'int',varbR))
    # e4.config(validate ="key", validatecommand =(reg, '%P', 'str',varbR))
    # e5.config(validate ="key", validatecommand =(reg, '%P', 'str',varbR))
    
    # e1.config(validate ="key", validatecommand =(reg, '%P', 'int',varb.get()))
    # e2.config(validate ="key", validatecommand =(reg, '%P', 'int',varb.get()))
    # e3.config(validate ="key", validatecommand =(reg, '%P', 'int',varb.get()))
    # e4.config(validate ="key", validatecommand =(reg, '%P', 'str',varb.get()))
    # e5.config(validate ="key", validatecommand =(reg, '%P', 'str',varb.get()))
    
    e1.config(validate ="key", validatecommand =(reg, '%P', 'int',varb))
    e2.config(validate ="key", validatecommand =(reg, '%P', 'int',varb))
    e3.config(validate ="key", validatecommand =(reg, '%P', 'int',varb))
    e4.config(validate ="key", validatecommand =(reg, '%P', 'str',varb))
    e5.config(validate ="key", validatecommand =(reg, '%P', 'str',varb))
    
    solve = tk.Button(mainwindow, text='solve!', command=lambda: [values()]).grid(row=7, column=1, sticky=tk.W, pady=4)
    
    
    

    def values():
        
        try:
            a = varb.get()
            print(a)
            
            readN = getN.get()
            readi0 = geti0.get()
            readr0 = getr0.get()
            # readbeta = float(getbeta.get())
            # readgamma = float(getgamma.get())
    
            # readbeta_ = getbeta.get()
            
            # if readbeta_[0] == '/':
            #     readbeta_ = readbeta_[1:]
            # readbeta = eval(readbeta_,{"builtins": {}})
            readbeta = eval(getbeta.get(),{"builtins": {}})
            readgamma = eval(getgamma.get(), {"builtins": {}})
            
            
            
            intN = int(readN)
            inti0 = int(readi0)
            intr0 = int(readr0)
            intbeta = float(readbeta)
            intgamma = float(readgamma)
            
            print('varb : ', varb.get(),
                  '\nN : ', intN,
                  '\niO : ',inti0,
                  '\nr0 : ',intr0,
                  '\nbeta : ',getbeta.get(),
                  '\ngamma : ',getgamma.get())
            
            # Total population, N.
            N = readN
            # Initial number of infected and recovered individuals, I0 and R0.
            I0, R0 = readi0, readr0
            # Everyone else, S0, is susceptible to infection initially.
            S0 = N - I0 - R0
            # Contact rate, beta, and mean recovery rate, gamma, (in 1/days).
            beta, gamma = readbeta, readgamma
            # A grid of time points (in days)
            t = np.linspace(0, 160, 160)
    
            # The SIR model differential equations.
            def deriv(y, t, N, beta, gamma):
                S, I, R = y
                dS = ((-beta * S * I) / N)
                dI = ((beta * S * I) / N) - (gamma * I)
                dR = (gamma * I)
                return dS, dI, dR
            
            # Initial conditions are S0, I0, R0
            # Integrate the SIR equations over the time grid, t.
            solve = odeint(deriv, (S0, I0, R0), t, args=(N, beta, gamma))
            S, I, R = solve.T
            
            # Plot the data on three separate curves for S(t), I(t) and R(t)
            fig = plt.figure(facecolor='w')
            ax = fig.add_subplot(111, facecolor='#dddddd', axisbelow=True)
            ax.plot(t, S/1000, 'b', alpha=0.5, lw=2, label='Susceptible')
            ax.plot(t, I/1000, 'r', alpha=0.5, lw=2, label='Infected')
            ax.plot(t, R/1000, 'g', alpha=0.5, lw=2, label='Recovered with immunity')
            ax.set_xlabel('Time /days')
            ax.set_ylabel('Number (1000s)')
            ax.set_ylim(0,1.2)
            ax.yaxis.set_tick_params(length=0)
            ax.xaxis.set_tick_params(length=0)
            ax.grid(b=True, which='major', c='w', lw=2, ls='-')
            legend = ax.legend()
            legend.get_frame().set_alpha(0.5)
            for spine in ('top', 'right', 'bottom', 'left'):
                ax.spines[spine].set_visible(False)
            plt.show()
            return
            
        except:
            print('maybe wrong values !!!!!!!!')
            return
        
    mainwindow.mainloop()
    
mainwindow()

do you mean you tried the gui version? yes the gui cannot take fractions as of yet — Landon, Sep 07 '21 at 17:26
So you used the gui version, with which values? and it worked? — Landon, Sep 07 '21 at 21:03
ok. im just confused why it wont work for me but it worked for you — Landon, Sep 08 '21 at 12:07
@Isa added different code above to use 2/7and 1/7 in input. If the answer its OK for You please tick it as accepted (I need the points ;-) !! ) — pippo1980, Sep 08 '21 at 17:45

Solving simple ODE system within tkinter GUI

1 Answers1

Linked