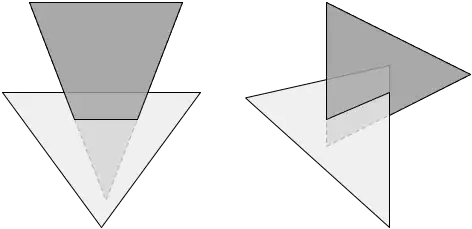
I implemented the algorithm described in Dynamic Collision Detection using Oriented Bounding Boxes for non-coplanar triangles only, which is based on the separating axis theorem.
Here's my GitHub repo with the code (in the file collision-tests.js) and a demo/test page:
The code is deliberately written to match the relevant portion of the 'Dynamic Collision' document. Below is the intersection test function (and the whole contents of the collision-tests.js file). Note that a three.js triangle object has a, b, and c properties for the triangle's three vertices.
/**
* @function
* @param {THREE.Triangle} t1 - Triangular face
* @param {THREE.Triangle} t2 - Triangular face
* @returns {boolean} Whether the two triangles intersect
*/
function doTrianglesIntersect(t1, t2) {
/*
Adapated from section "4.1 Separation of Triangles" of:
- [Dynamic Collision Detection using Oriented Bounding Boxes](https://www.geometrictools.com/Documentation/DynamicCollisionDetection.pdf)
*/
// Triangle 1:
var A0 = t1.a;
var A1 = t1.b;
var A2 = t1.c;
var E0 = A1.clone().sub(A0);
var E1 = A2.clone().sub(A0);
var E2 = E1.clone().sub(E0);
var N = E0.clone().cross(E1);
// Triangle 2:
var B0 = t2.a;
var B1 = t2.b;
var B2 = t2.c;
var F0 = B1.clone().sub(B0);
var F1 = B2.clone().sub(B0);
var F2 = F1.clone().sub(F0);
var M = F0.clone().cross(F1);
var D = B0.clone().sub(A0);
function areProjectionsSeparated(p0, p1, p2, q0, q1, q2) {
var min_p = Math.min(p0, p1, p2),
max_p = Math.max(p0, p1, p2),
min_q = Math.min(q0, q1, q2),
max_q = Math.max(q0, q1, q2);
return ((min_p > max_q) || (max_p < min_q));
}
// Only potential separating axes for non-parallel and non-coplanar triangles are tested.
// Seperating axis: N
{
var p0 = 0,
p1 = 0,
p2 = 0,
q0 = N.dot(D),
q1 = q0 + N.dot(F0),
q2 = q0 + N.dot(F1);
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
// Separating axis: M
{
var p0 = 0,
p1 = M.dot(E0),
p2 = M.dot(E1),
q0 = M.dot(D),
q1 = q0,
q2 = q0;
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
// Seperating axis: E0 × F0
{
var p0 = 0,
p1 = 0,
p2 = -(N.dot(F0)),
q0 = E0.clone().cross(F0).dot(D),
q1 = q0,
q2 = q0 + M.dot(E0);
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
// Seperating axis: E0 × F1
{
var p0 = 0,
p1 = 0,
p2 = -(N.dot(F1)),
q0 = E0.clone().cross(F1).dot(D),
q1 = q0 - M.dot(E0),
q2 = q0;
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
// Seperating axis: E0 × F2
{
var p0 = 0,
p1 = 0,
p2 = -(N.dot(F2)),
q0 = E0.clone().cross(F2).dot(D),
q1 = q0 - M.dot(E0),
q2 = q1;
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
// Seperating axis: E1 × F0
{
var p0 = 0,
p1 = N.dot(F0),
p2 = 0,
q0 = E1.clone().cross(F0).dot(D),
q1 = q0,
q2 = q0 + M.dot(E1);
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
// Seperating axis: E1 × F1
{
var p0 = 0,
p1 = N.dot(F1),
p2 = 0,
q0 = E1.clone().cross(F1).dot(D),
q1 = q0 - M.dot(E1),
q2 = q0;
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
// Seperating axis: E1 × F2
{
var p0 = 0,
p1 = N.dot(F2),
p2 = 0,
q0 = E1.clone().cross(F2).dot(D),
q1 = q0 - M.dot(E1),
q2 = q1;
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
// Seperating axis: E2 × F0
{
var p0 = 0,
p1 = N.dot(F0),
p2 = p1,
q0 = E2.clone().cross(F0).dot(D),
q1 = q0,
q2 = q0 + M.dot(E2);
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
// Seperating axis: E2 × F1
{
var p0 = 0,
p1 = N.dot(F1),
p2 = p1,
q0 = E2.clone().cross(F1).dot(D),
q1 = q0 - M.dot(E2),
q2 = q0;
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
// Seperating axis: E2 × F2
{
var p0 = 0,
p1 = N.dot(F2),
p2 = p1,
q0 = E2.clone().cross(F2).dot(D),
q1 = q0 - M.dot(E2),
q2 = q1;
if (areProjectionsSeparated(p0, p1, p2, q0, q1, q2))
return false;
}
return true;
}