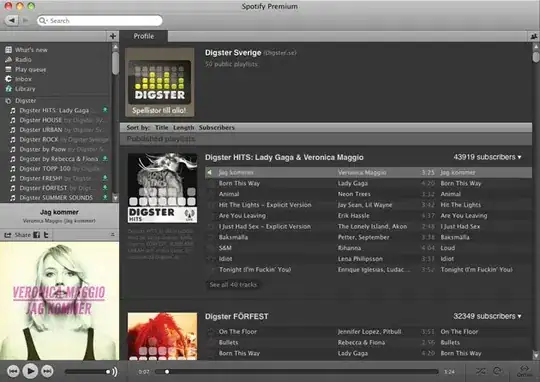
There are dozens of answers on here about how to fit an ellipse to your points, but none seem to suggest ways to quantify the fit. Here's some points and the ellipse fitted from this answer:
import numpy as np
from skimage.measure import EllipseModel
from matplotlib.patches import Ellipse
import matplotlib.pyplot as plt
x1 = [710.804, 710.117, 709.565, 709.036, 707.839, 707.424, 706.889, 705.913, 705.037, 704.58, 703.758,704.105, 704.552, 704.833, 705.204, 706.027, 706.932, 708.041, 708.849, 709.379, 709.797, 710.272,710.494, 710.871, 711.033, 711.018, 710.804]
y1 = [493.076, 491.902, 491.409, 490.947, 490.396, 491.456, 491.887, 492.917, 494.022, 494.882, 496.085,496.934, 497.723, 498.17, 498.656, 498.929, 499.248, 499.156, 498.768, 498.487, 497.853, 497.212,496.753, 495.957, 495.003, 493.997, 493.076]
points = list(zip(x1,y1))
print(points)
a_points = np.array(points)
x = a_points[:, 0]
y = a_points[:, 1]
ell = EllipseModel()
ell.estimate(a_points)
residuals = ell.residuals(a_points)
xc, yc, a, b, theta = ell.params
print("center = ", (xc, yc))
print("angle of rotation = ", theta)
print("axes = ", (a,b))
print('residuals= ', residuals)
fig, axs = plt.subplots(2, 1, sharex=True, sharey=True)
axs[0].scatter(x,y)
axs[1].scatter(x, y)
axs[1].scatter(xc, yc, color='red', s=100)
axs[1].set_xlim(x.min(), x.max())
axs[1].set_ylim(y.min(), y.max())
ell_patch = Ellipse((xc, yc), 2*a, 2*b, theta*180/np.pi,
edgecolor='red', facecolor='none')
axs[1].add_patch(ell_patch)
plt.show()
center = (707.7248344321281, 495.2907644989805)
angle of rotation = 2.1051122302898926
axes = (4.783618808884847, 2.92938238506285)
residuals= [0.4031933 0.60237637 0.44816215 0.03196744 0.77430711 0.00493033 0.04060345 0.07892221 0.03482433 0.08585788 0.55088573 0.11629398 0.2794519 0.43588704 0.52172484 0.71671995 0.32973538 0.0389334 0.19938749 0.35342937 0.2419931 0.24903068 0.1998942 0.18446699 0.02005871 0.18610954 0.4031933 ]
Once I have created a fit, I want to calculate how well it fits the points. I can calculate the residuals using an EllipseModel function. I'm not sure how to use them for this purpose though. I can't use Pearson's correlation as it compares 1D lists. I thought I could calculate the closest point on the ellipse to each of my points by using the ratio of the residual to the distance from point to the ellipse centre of mass and transforming X and Y accordingly. I then thought to try dot product but that seems to require vectors, not points.
Can someone suggest a way to score the fit of the ellipse model?