Why overlaying Beta distribution on a histogram fails for small sample sizes?

Question

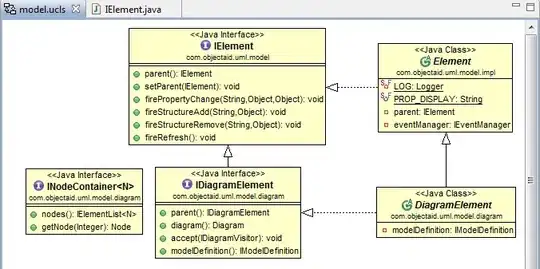
For those without a statistics background but who could assist with coding: I have multiple small datasets (around 30 to 200 rows each) and need to determine the best-fitting distribution. One approach is visual inspection, Here I focus on the Normal and Beta distributions for sake of simplicity.

The Beta distribution has a constraint: data must be within [0, 1]. Other distributions don't have such a restriction. In case data falls out of this range, we can scale it to [0, 1] and that is no problem.

JMP (which is a strong statistical software) works fine no matter how big of data set it is working with. I'm trying to replicate the same graphs in R. When dealing with small datasets (less than 80 rows), I get meaningless results in R. Larger datasets (around 5000 data points) produce consistent results in both R and JMP. Any ideas?

Plz remember all my datasets are small so I get meaningless graphs in R. I am unable to share my data so we work with generated data.

I have the following code:

get_histogram <- function(data_set, column_name, bin_width) {
  
  colname <- as_label(enquo(column_name))
  x <- data_set[[colname]]
  shift <- min(x)
  scale <- diff(range(x))
  norm_it <- function(x) (x - shift + 1e-8) / (diff(range(x)) + 2e-8)
  
  beta_par    <- fitdistr(norm_it(x), dbeta, 
                          start = list(shape1 = 1, shape2 = 1))$estimate
  
  ggplot(data_set, aes(x = {{ column_name }})) +
    geom_histogram(aes(y = after_stat(density)), binwidth = bin_width, 
                   fill = "lightblue", colour="black") +
    stat_function(fun = dnorm, args = list(mean = mean(x), sd = sd(x)), 
                  mapping = aes(colour = "Normal")) +
    stat_function(fun = function(x) dbeta(norm_it(x), beta_par[1], beta_par[2])/(scale),
                  mapping = aes(color = "Beta")) +
    scale_colour_manual("Distribution", 
                        values = c("red", "blue"))
}

I've kept a section of my code that overlays two distributions (Beta and Normal). When I generate random data with fewer than 80 points, even if it's Beta-distributed, the graph doesn't make sense. This issue doesn't happen with more data points. Note that most of my real datasets have fewer than 80 rows, so the problem remains with real data.

set.seed(2122)
test_dt <- rnorm(50, 30 , 2)
new_col <- sample(size = 50, x= c("a", "b", "c"), replace = TRUE)
df <- data.frame(test_dt, new_col)
rm(test_dt)
rm(new_col)

get_histogram(df, test_dt, .05)

When I fit a beta distribution in JMP, I get a nice result, but R's output is completely incorrect.

This doesn't occur with more data, like 5000 points, where R and JMP outputs are very similar, as shown:

I have two questions:

1. In stat_function(), should the denominator be / scale or / (scale + shift) when overlaying the Beta distribution? Some argue for the first option, even though the second one seems mathematically correct.
2. Why does this code struggle with small datasets? Typically, any sample larger than 30 can fit a distribution, but this isn't the case here. Any insights? Grateful for your help with this R issue.

Compare the y-axes in these photos. The first one displays density probabilities of up to 400, which is statistically meaningless. Identifying the cause of this issue could be the answer to all my questions.

Answer 1

Based on the comment from @Mrflick the following code produces a similar output as above but of course, without knowing which distribution JMP uses it is impossible to get the exact same results.

The solution uses the 4-parameter generalized beta distribution which could be the same one as from JMP. The function eBeta_ab(...) estimates the parameters and together with dBeta_ab() comes from the ExtDist package. The estimated parameters are close to the ones in JMP. Since the generalized beta does not have the same strict boundaries as the beta, we do not need to shift or scale anything.

library(fitdistrplus)
library(ExtDist)
library(ggplot2)

get_histogram <- function(data_set, column_name, bin_width) {
  
  colname <- as_label(enquo(column_name))
  x <- data_set[[colname]]
  beta_par <- eBeta_ab(x)
  print(beta_par)
  ggplot(data_set, aes(x = {{ column_name }})) +
    geom_histogram(aes(y = after_stat(density)), binwidth = bin_width, 
                   fill = "lightblue", colour="black") +
    stat_function(fun = dnorm, args = list(mean = mean(x), sd = sd(x)), 
                  mapping = aes(colour = "Normal")) +
    stat_function(fun = function(x) dBeta_ab(x, 
                                             beta_par[1]$shape1, 
                                             beta_par[2]$shape2, 
                                             beta_par[3]$a, 
                                             beta_par[4]$b),
                  mapping = aes(color = "Generalized Beta")) +
    scale_colour_manual("Distribution", 
                        values = c("red", "blue"))
}

set.seed(2122)
test_dt <- rnorm(50, 30 , 2)
new_col <- sample(size = 50, x= c("a", "b", "c"), replace = TRUE)
df <- data.frame(test_dt, new_col)

get_histogram(df, test_dt, .5)

Answer 2

Mainly to answer your Q2:

I don't think there is any problem with the plotting as of course you can have densities greater than 1 e.g. dnorm(0,0,0.1).

But you do have problems with the numerical optimisation from fitdistr. If I look at your estimates for beta_par, I get

beta_par
shape1    shape2 
0.6743766 0.5413656 

This explains why you get the apparent blowing up on the right-hand side of your plot. And also explains why it works well when you have more data - the optimisation finds the correct solution easily.

So what can you do? There are other packages for fitting e.g. fitdistrplus as I read about here. I tried it quickly but I didn't get any improvement - you may need to use more advanced options e.g. increase number of iterations, reduce tolerances, try another method. They have a nice vignette about which optimisation algorithm to choose including a beta distribution example.

Answer 3

In the plots you shared that were generated from JMP, the beta function is using 4 parameters and reviewing the code you shared for R, the beta function only uses 2 parameters. If they were using the same # of parameters and the same #s, you would get identical charts.