Efficient evaluation of a function at every cell of a NumPy array

Question

Given a NumPy array A, what is the fastest/most efficient way to apply the same function, f, to every cell?

1. Suppose that we will assign to A(i,j) the f(A(i,j)).

2. The function, f, doesn't have a binary output, thus the mask(ing) operations won't help.

Is the "obvious" double loop iteration (through every cell) the optimal solution?

Answer 1

You could just vectorize the function and then apply it directly to a Numpy array each time you need it:

import numpy as np

def f(x):
    return x * x + 3 * x - 2 if x > 0 else x * 5 + 8

f = np.vectorize(f)  # or use a different name if you want to keep the original f

result_array = f(A)  # if A is your Numpy array

It's probably better to specify an explicit output type directly when vectorizing:

f = np.vectorize(f, otypes=[np.float])

Answer 2

A similar question is: Mapping a NumPy array in place. If you can find a ufunc for your f(), then you should use the out parameter.

Answer 3

If you are working with numbers and f(A(i,j)) = f(A(j,i)), you could use scipy.spatial.distance.cdist defining f as a distance between A(i) and A(j).

Answer 4

I believe I have found a better solution. The idea to change the function to python universal function (see documentation), which can exercise parallel computation under the hood.

One can write his own customised ufunc in C, which surely is more efficient, or by invoking np.frompyfunc, which is built-in factory method. After testing, this is more efficient than np.vectorize:

f = lambda x, y: x * y
f_arr = np.frompyfunc(f, 2, 1)
vf = np.vectorize(f)
arr = np.linspace(0, 1, 10000)

%timeit f_arr(arr, arr) # 307ms
%timeit f_arr(arr, arr) # 450ms

I have also tested larger samples, and the improvement is proportional. For comparison of performances of other methods, see this post

Answer 5

When the 2d-array (or nd-array) is C- or F-contiguous, then this task of mapping a function onto a 2d-array is practically the same as the task of mapping a function onto a 1d-array - we just have to view it that way, e.g. via np.ravel(A,'K').

Possible solution for 1d-array have been discussed for example here.

However, when the memory of the 2d-array isn't contiguous, then the situation a little bit more complicated, because one would like to avoid possible cache misses if axis are handled in wrong order.

Numpy has already a machinery in place to process axes in the best possible order. One possibility to use this machinery is np.vectorize. However, numpy's documentation on np.vectorize states that it is "provided primarily for convenience, not for performance" - a slow python function stays a slow python function with the whole associated overhead! Another issue is its huge memory-consumption - see for example this SO-post.

When one wants to have a performance of a C-function but to use numpy's machinery, a good solution is to use numba for creation of ufuncs, for example:

# runtime generated C-function as ufunc
import numba as nb
@nb.vectorize(target="cpu")
def nb_vf(x):
    return x+2*x*x+4*x*x*x

It easily beats np.vectorize but also when the same function would be performed as numpy-array multiplication/addition, i.e.

# numpy-functionality
def f(x):
    return x+2*x*x+4*x*x*x

# python-function as ufunc
import numpy as np
vf=np.vectorize(f)
vf.__name__="vf"

See appendix of this answer for time-measurement-code:

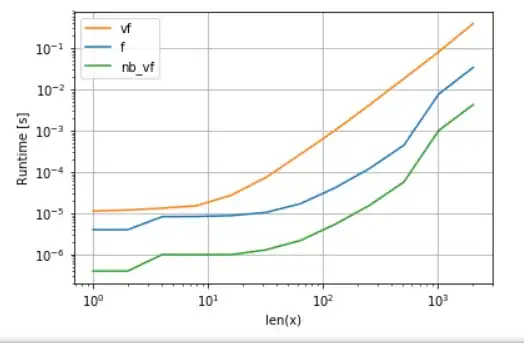
Numba's version (green) is about 100 times faster than the python-function (i.e. np.vectorize), which is not surprising. But it is also about 10 times faster than the numpy-functionality, because numbas version doesn't need intermediate arrays and thus uses cache more efficiently.

---

While numba's ufunc approach is a good trade-off between usability and performance, it is still not the best we can do. Yet there is no silver bullet or an approach best for any task - one has to understand what are the limitation and how they can be mitigated.

For example, for transcendental functions (e.g. exp, sin, cos) numba doesn't provide any advantages over numpy's np.exp (there are no temporary arrays created - the main source of the speed-up). However, my Anaconda installation utilizes Intel's VML for vectors bigger than 8192 - it just cannot do it if memory is not contiguous. So it might be better to copy the elements to a contiguous memory in order to be able to use Intel's VML:

import numba as nb
@nb.vectorize(target="cpu")
def nb_vexp(x):
    return np.exp(x)

def np_copy_exp(x):
    copy = np.ravel(x, 'K')
    return np.exp(copy).reshape(x.shape) 

For the fairness of the comparison, I have switched off VML's parallelization (see code in the appendix):

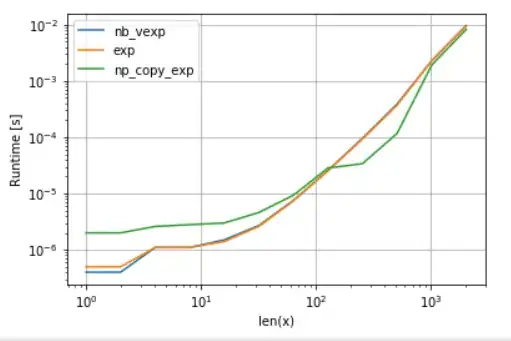
As one can see, once VML kicks in, the overhead of copying is more than compensated. Yet once data becomes too big for L3 cache, the advantage is minimal as task becomes once again memory-bandwidth-bound.

On the other hand, numba could use Intel's SVML as well, as explained in this post:

from llvmlite import binding
# set before import
binding.set_option('SVML', '-vector-library=SVML')

import numba as nb

@nb.vectorize(target="cpu")
def nb_vexp_svml(x):
    return np.exp(x)

and using VML with parallelization yields:

numba's version has less overhead, but for some sizes VML beats SVML even despite of the additional copying overhead - which isn't a bit surprise as numba's ufuncs aren't parallelized.

---

Listings:

A. comparison of polynomial function:

import perfplot
perfplot.show(
    setup=lambda n: np.random.rand(n,n)[::2,::2],
    n_range=[2**k for k in range(0,12)],
    kernels=[
        f,
        vf, 
        nb_vf
        ],
    logx=True,
    logy=True,
    xlabel='len(x)'
    ) 

B. comparison of exp:

import perfplot
import numexpr as ne # using ne is the easiest way to set vml_num_threads
ne.set_vml_num_threads(1)
perfplot.show(
    setup=lambda n: np.random.rand(n,n)[::2,::2],
    n_range=[2**k for k in range(0,12)],
    kernels=[
        nb_vexp, 
        np.exp,
        np_copy_exp,
        ],
    logx=True,
    logy=True,
    xlabel='len(x)',
    )

Answer 6

All above answers compares well, but if you need to use custom function for mapping, and you have numpy.ndarray, and you need to retain the shape of array.

I have compare just two, but it will retain the shape of ndarray. I have used the array with 1 million entries for comparison. Here I use square function. I am presenting the general case for n dimensional array. For two dimensional just make iter for 2D.

import numpy, time

def A(e):
    return e * e

def timeit():
    y = numpy.arange(1000000)
    now = time.time()
    numpy.array([A(x) for x in y.reshape(-1)]).reshape(y.shape)        
    print(time.time() - now)
    now = time.time()
    numpy.fromiter((A(x) for x in y.reshape(-1)), y.dtype).reshape(y.shape)
    print(time.time() - now)
    now = time.time()
    numpy.square(y)  
    print(time.time() - now)

Output

>>> timeit()
1.162431240081787    # list comprehension and then building numpy array
1.0775556564331055   # from numpy.fromiter
0.002948284149169922 # using inbuilt function

here you can clearly see numpy.fromiter user square function, use any of your choice. If you function is dependent on i, j that is indices of array, iterate on size of array like for ind in range(arr.size), use numpy.unravel_index to get i, j, .. based on your 1D index and shape of array numpy.unravel_index

This answers is inspired by my answer on other question here