I have a list of points that make a curve, and I would like to reduce the number of points, but still keep the overall shape of the curve.
Basically, I want to go from this:
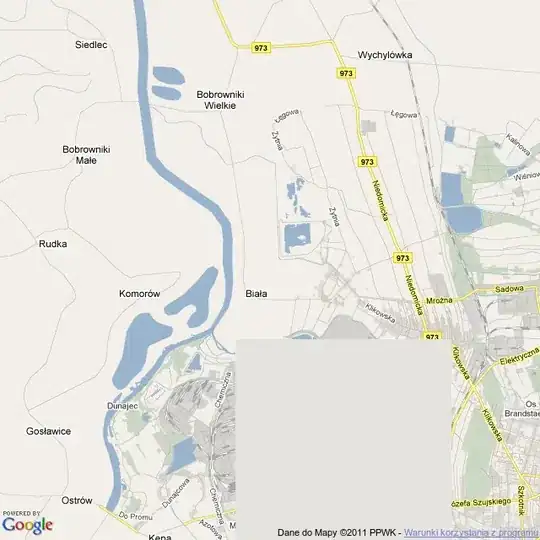
To this:
So the algorithm would remove the points that are redundant but preserve those that really define the shape (like the points at the bottom of the curve). Is there any known algorithm to do that? I expect there is but I'm not sure what to search for on Google. Any help would be appreciated.
