How do I derive a Voronoi diagram given its point set and its Delaunay triangulation?

Question

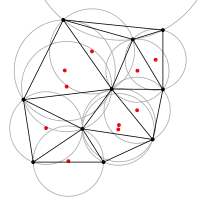
I'm working on a game where I create a random map of provinces (a la Risk or Diplomacy). To create that map, I'm first generating a series of semi-random points, then figuring the Delaunay triangulations of those points.

With that done, I am now looking to create a Voronoi diagram of the points to serve as a starting point for the province borders. My data at this point (no pun intended) consists of the original series of points and a collection of the Delaunay triangles.

I've seen a number of ways to do this on the web, but most of them are tied up with how the Delaunay was derived. I'd love to find something that doesn't need to be integrated to the Delaunay, but can work based off the data alone. Failing that, I'm looking for something comprehensible to a relative geometry newbie, as opposed to optimal speed. Thanks!

score 23 · Accepted Answer · edited May 10 '12 at 13:12

23

The Voronoi diagram is just the dual graph of the Delaunay triangulation.

So, the edges of the Voronoi diagram are along the perpendicular bisectors of the edges of the Delaunay triangulation, so compute those lines.
Then, compute the vertices of the Voronoi diagram by finding the intersections of adjacent edges.
Finally, the edges are then the subsets of the lines you computed which lie between the corresponding vertices.

Note that the exact code depends on the internal representation you're using for the two diagrams.

edited May 10 '12 at 13:12

menjaraz

7,551
4
41
81

answered Sep 17 '08 at 16:59

Adam Rosenfield

390,455
97
512
589

27

You can also find the dual (ie. Voronoi diagram) just by computing the circumcentres of all the triangles, and connecting any two circumcentres whose triangles share an edge. – batty May 01 '09 at 03:22
6

As suggested in the above comment, I would do it in two steps: 1. Compute the circumcenter of every Delaunay triangle -> these are the Voronoi vertices. See http://en.wikipedia.org/wiki/Circumscribed_circle#Circumscribed_circles_of_triangles 2. For every Delaunay edge, compute a Voronoi edge: the segment connecting the circumcenters of the two neighboring Delaunay triangles. – balint.miklos Jul 10 '09 at 12:43
8

@balint.miklos What to do with outer sites/triangles? – Tomilov Anatoliy May 03 '16 at 12:20

score 9 · Answer 2 · answered Sep 17 '08 at 17:13

9

If optimal speed is not a consideration, the following psuedo code will generate a Voronoi diagram the hard way:

for yloop = 0 to height-1
  for xloop = 0 to width-1

    // Generate maximal value
    closest_distance = width * height

    for point = 0 to number_of_points-1
      // calls function to calc distance
      point_distance = distance(point, xloop, yloop)

      if point_distance < closest_distance
        closest_point = point
      end if
    next

  // place result in array of point types
  points[xloop, yloop] = point

  next
next

Assuming you have a 'point' class or structure, if you assign them random colours, then you'll see the familiar voronoi pattern when you display the output.

answered Sep 17 '08 at 17:13

Alexandra Franks

2,982
1
19
23

That's all nice and dandy, but I don't see any use for a Voronoi diagram generated as an image. Maybe there is one? – Tara Feb 05 '15 at 15:45
2

Not as an image per se, but I've used it for procedural tile-based world generation (where each tile is determined by the cell to which it belongs). – PixelArtDragon May 08 '16 at 04:55
Shaders use this approach (kind of) most of the time (just for graphical output though). – Trap Dec 21 '22 at 21:06

score 3 · Answer 3 · answered Oct 02 '12 at 14:58

After trying to use this thread as a source for answers to my own similar question, I found that Fortune's algorithm — likely because it is the most popular & therefore most documented — was the easiest to understand.

The Wikipedia article on Fortune's algorithm keeps fresh links to source code in C, C#, and Javascript. All of them were top-notch and came with beautiful examples.

score 0 · Answer 4 · answered May 23 '23 at 16:47

Start by obtaining the Delaunay triangulation first. The center of each triangle's circumcircle is a vertex (point) for the Voronoi tesselation. Then simply connect the centers of all the circumcircles of the neighboring triangles to derive the tesselation. From Wikipedia, this is shown as follows.

First, get all the circumcircle centers (from all the triangles) - i.e., the red points:

Next, connect the centers of circumcircles for each neighboring triangle together with lines to get the tesselation:

score 0 · Answer 5 · answered Sep 17 '08 at 17:14

0

Each of your Delaunay triangles contains a single point of the Voronoi diagram.

You can compute this point by finding the intersection of the three perpendicular bisectors for each triangle.

Your Voronoi diagram will connect this set of points, each with it's nearest three neighbors. (each neighbor shares a side of the Delaunay triangle)

How do you plan on approaching the edge cases?

answered Sep 17 '08 at 17:14

Arc the daft

225
1
2

Note that although for every Delaunay triangle corresponds one Voronoi vertex, this vertex **can be outside the triangle**, as well. see an example here: http://www.mathopenref.com/trianglecircumcenter.html – balint.miklos Jul 10 '09 at 12:46

How do I derive a Voronoi diagram given its point set and its Delaunay triangulation?

5 Answers5

Linked