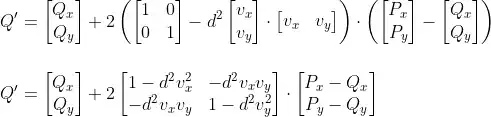How to calculate the mirror point along a line?

Question

In 2D plane, I have a point and a line. How to get the mirror point along this line?

Answer 1

When things like that are done in computer programs, one of the issues you might have to deal with is to perform these calculations using integer arithmetic only (or as much as possible), assuming the input is in integers. Doing this in integers as much as possible is a separate issue that I will not cover here.

The following is a "mathematical" solution, which if implemented literally will require floating-point calculations. I don't know whether this is acceptable in your case. You can optimize it to your taste yourself.

(1) Represent your line L by

A * x + B * y + C = 0

equation. Note that vector (A, B) is the normal vector of this line.

For example, if the line is defined by two points X1(x1, y1) and X2(x2, y2), then

A = y2 - y1
B = -(x2 - x1)
C = -A * x1 - B * y1

(2) Normalize the equation by dividing all coefficients by the length of vector (A, B). I.e. calculate the length

M = sqrt(A * A + B * B)

and then calculate the values

A' = A / M
B' = B / M
C' = C / M

The equation

A' * x + B' * y + C' = 0

is still an equivalent equation of your line L except that now the normal vector (A', B') is a unit vector.

(3) Take your point P(px, py) and calculate the value

D = A' * px + B' * py + C'

This will give you the signed distance D from your point P to your line L. In other words, this is the distance from P to the closest point on L (we don't really care about the closest point itself, we just need the distance).

The sign says which side of the line L the point P lies on. If P lies on the same side the vector (A', B') is pointing to ("positive" side), the distance is positive. If P lies on the other side ("negative" side), the distance is negative.

(4) In order to find your mirror point P'(px', py') you need to move your point P by the absolute distance |2 * D| across the line L to the other side.

"Across the line" really means that if point P was lying on the "positive" side of L, then we have to move it against the direction of vector (A', B') to the "negative" side. And vice versa, if point P was lying on the "negative" side of L, then we have to move it in the direction of vector (A', B') to the "positive" side.

This can simply be expressed as moving the point the distance of -2 * D (note the minus) in the direction of vector (A', B').

That means that

px' = px - 2 * A' * D
py' = py - 2 * B' * D

gives you your mirror point P'(px', py').

---

Alternatively, you can use an approach based on finding the actual closest point N on line L and then reflecting your point P with relation to N. This is already suggested in other answers, I'll just describe how I'd do it.

(1) Build an equation

A*x + B*y + C = 0

for your line L exactly as described in step 1 above. There's no need to normalize this equation.

(2) Build an equation for the perpendicular line that passes through P. Let's say that perpendicular line is represented by

D*x + E*y + F = 0

The D and E coefficients are known right away

D = B
E = -A

while F can be calculated by substituting point P into the equation

F = -D*px - E*py

(3) Find the intersection of these two lines by solving the system of two linear equations

A*x + B*y = -C
D*x + E*y = -F

Cramer's rule works very well in this case. The formula given in Line intersection article in Wikipedia are nothing else than an application of Cramer's rule to this system.

The solution gives you the nearest point N(nx, ny) we were looking for.

(4) Now just calculate

px' = nx + (nx - px)
py' = ny + (ny - py)

to find your point P'(px', py').

Note that this approach can be almost entirely implemented in integers. The only step that might lose precision is division inside the Cramer's rule at step 3. Of course, as usual, the price you'll have to pay for "almost integral" solution is the need for large-number arithmetic. Even coefficients C and F can overflow, not even mentioning computations inside Cramer's rule formulae.

Answer 2

The details depend on how your line is represented. If you represent it as an arbitrary point P on the line together with a unit column vector n along the line, then the mirror point Q' to any point Q is given by:

Q' = Q + 2(I - nn^T)(P - Q)

(Here, I is the 2x2 identity matrix, n^T is the transpose of n (treating n as a 2x1 matrix), and nn^T is the 2x2 matrix formed by standard matrix multiplication of n with n^T.) It's not too hard to show that Q' will not change if you move P anywhere on the line.

It's not hard to convert other line representations into a point/unit vector representation.

Answer 3

Suppose the equation of the line is ax + by + c = 0. Now imagine a line perpendicular to it, which can be represented by -bx + ay + d = 0 (product of slopes of two perpendicular lines is -1). Now the problem is to find d. Put the co-ordinate of the point on the second line, and you'll get the value of d easily.

The second part is, to find a point on the second line which is equidistant as the first point from the first line. For that, you can find the intersection of the two lines. Calculate the differences in x and y of the given point and the intersection point. Now add those to the x and y value of the intersecting point. That gives the point you need (you may need to negate the differences - that's up to the order of subtraction you use).

Answer 4

I develop JS code which calculate formula from Ted Hop answer: Q' = Q + 2(I - nn^T)(P - Q) transformed to

Q' = Q + 2(I - d²vv^T)(P - Q)

Where column vector v=R-P is parallel to line but is not unit (like n), P and R are two arbitrary line points; the vv^T is outer product; I is identity matrix; the d=1/sqrt(vx*vx + vy*vy) is inverse length of v. Because we use d² (=r in code) we can optimize calculations by omit sqrt

// 2D Points P=[x,y] and R=[x,y] are arbitrary points on line, 
// Q=[x,y] is point for which we want to find reflection
// returns solution vector [x,y] 
function mirror(Q,[P,R]) {
  let [vx,vy]= [ R[0]-P[0], R[1]-P[1] ];
  let [x,y]  = [ P[0]-Q[0], P[1]-Q[1] ];
  let r= 1/(vx*vx+vy*vy);
  return [ Q[0] +2*(x -x*vx*vx*r -y*vx*vy*r), 
           Q[1] +2*(y -y*vy*vy*r -x*vx*vy*r)  ];
}

console.log( mirror([3,2], [[2,4],[4,5]]) )

Latex formulas used in this asnwer (I left them here for passible future answer editions)
<pre>
\\
Q' = \begin{bmatrix}
Q_x \\ 
Q_y
\end{bmatrix}
+2 \left( 
  \begin{bmatrix}
  1 & 0\\ 
  0 & 1
  \end{bmatrix}
  -
  d^2\begin{bmatrix}
  v_x\\  v_y \end{bmatrix}
  \cdot
  \begin{bmatrix} v_x & v_y  \end{bmatrix}
\right )
\cdot
\left(\begin{bmatrix} P_x\\  P_y \end{bmatrix} - \begin{bmatrix} Q_x\\  Q_y \end{bmatrix}\right )

\\
\\
\\

Q' = \begin{bmatrix}
Q_x \\ 
Q_y
\end{bmatrix}
+2
  \begin{bmatrix}
  1 - d^2v_x^2  & -d^2v_xv_y\\ 
  -d^2v_xv_y & 1 - d^2v_y^2
  \end{bmatrix}
  
\cdot
\begin{bmatrix} P_x-Q_x\\  P_y-Q_y \end{bmatrix} 

</pre>

Answer 5

Compute the closest point on the line to the point in question. Then invert the direction of the vector between those points and add it to the closest point on the line. Voilà, you have found the mirror point.

Answer 6

I assume you have the location of the point, and an equation for your line, i.e.

P=(x1,y1) and y = ax + b

First, the obvious case where a=0 (i.e. line parallel to the x axis) yields

P'(x2,y2), with x2 = x1, y2 = y1 + 2(b-y1)

For the more general case,

1. Get the generic equation for a line orthogonal to yours: y = cx + d, with ac = -1

   ==> c = -1/a

2. Determine b so that P belongs to the orthogonal line: y1 = -x1/a + d

   ==> d = y1 + x1/a

3. Get the intersection between the two lines: y = -x/a + y1 + x1/a = ax + b

   ==> x = (y1 + x1/a -b)/(a+1/a), y = a(y1 + x1/a -b)/(a+1/a) + b

4. Get the vector between the intersection and your point P, add that to the intersection point to obtain the mirror point P'.

   ==> P'(x2,y2), with x2 = x1 + 2((y1 + x1/a -b)/(a+1/a) - x1) y2 = y1 + 2(a(y1 + x1/a -b)/(a+1/a) + b - y1)

Some steps can be simplified but this is the general idea. I did the algebra while typing, so there could be mistakes. If you find one, please let me know.

Answer 7

I have done exactly this for another system I have built.. There's a lot more than this in my code; so I hope I have extracted all the necessary bits... Line.ClosestPoint(Point pt) is the method you want...

The algorithm is based on the idea that the slope of a line perpindicular to any given line is the negative multiplicative reciprocal of the slope of the given line. i.e., if one line has slope m, then the other line has slope -1/m. So all you need to do is form a line through the point with slope equal to -1/m and find the intersection of this line with the original line.

public class Line
{
    protected const double epsilon = 1.0e-8;

    public Point Anchor { get; set; }

    public double Slope { get; set; }

    public virtual Point ClosestPoint(Point pt)
    { return Intersection(Make(pt, -1 / Slope)); }

    protected Line(Point anchor, double slope)
    {
        Anchor = anchor;
        Slope = slope;
    }

    public static Line Make(Point anchor, double slope)
    { return new Line(anchor, slope); }

    public virtual Point Intersection(Line line)
    {
        if (lib.Within(line.Slope, Slope, epsilon))              
            if( lib.Within(line.YIntcpt, YIntcpt, epsilon))
                // code for NoInterceptException not included
                throw new NoInterceptException(
                    "The two lines overlap.");
            else return Point.NullPoint;
        // ----------------------------------------
        double tm = Slope, om = line.Slope,
            tx = Anchor.X, ty = Anchor.Y,
            ox = line.Anchor.X, oy = line.Anchor.Y;

        var x = double.IsInfinity(tm) ? tx :
                double.IsInfinity(om) ? ox :
                   (tm * tx - om * ox + oy - ty) /
                          (tm - om);

        var y = double.IsInfinity(tm) ?
               om * (x - ox) + oy :
               tm * (x - tx) + ty;

        return Point.Make(x, y);
    }
}

public struct Point
{
    const double epsilon = 1.0e-12;
    private readonly bool isDef;
    private readonly double y;
    private readonly double x;
    public bool HasValue { get { return isDef; } }
    public bool IsNull { get { return !isDef; } }

    private Point(double xValue, double yValue)
    { x = xValue; y = yValue; isDef = true; }
    public static Point Make(double x, double y)
    { return new Point(x, y); }

    public double X 
    {
        get
        {
                  // code for AlgebraicException not included
            if (IsNull) throw new AlgebraicException("Null Point Object"); 
            return x;
        }
    }
    public double Y
    {
        get
        {
                  // code for AlgebraicException not included
            if (IsNull) throw new AlgebraicException("Null Point Object");
            return y;
        }
    }

    public static Point NullPoint { get { return new Point();}}

    //  Other functionality

} 

Answer 8

You can use a simple formula to find this. First you have to write the formula of the line using

ax+by+c=0

lets say your line is y=x. and the point you'r trying to mirror is (3,2). we all know it's gonna become (2,3) anyway write y=x in standard form, which will become like this :

y-x=0

now use this formula and insert the values of the point instead of the x and y.

    (ax+by+c)/a^2+b^2
    (a^2 means a square.)

you will get a value, so let's name it K. in this instance where the point is (3,2) and the line is y-x=0, K would equal to:

(-3+2)/(1+1)= -1/2

now to calculate the new coordinates all you have to do is insert the values in this formula:

 x-2ak
 y-2bk

where x and y are the original coordinates and a and b are the values used in the original formula of the line (y-x=0 a=-1, b=1, c=0) so the value we get is:

3 - 2 x -1 x -1/2 = 3-1 = 2
2 - 2 x +1 x -1/2 = 2+1 = 3

Answer 9

Function mirrorPointAlongLine(line_x1 As Double, line_y1 As Double, line_x2 As Double, line_y2 As Double, x3 As Double, y3 As Double, ByRef xRet As Double, ByRef yRet As Double) As Boolean
'returns corrdinates of the point
'https://math.stackexchange.com/questions/65503/point-reflection-over-a-line

'A * x + B * y + C = 0
'y=Ax+c

Dim dx As Double, dy As Double, a As Double, b As Double
dx = line_x2 - line_x1
dy = line_y2 - line_y1

a = (dx * dx - dy * dy) / (dx * dx + dy * dy)
b = 2 * dx * dy / (dx * dx + dy * dy)
xRet = Round(a * (x3 - line_x1) + b * (y3 - line_y1) + line_x1)
yRet = Round(b * (x3 - line_x1) - a * (y3 - line_y1) + line_y1)

End Function