java string permutations and combinations lookup

Question

I'm writing an Android word app. My code includes a method that would find all combinations of the string and the substrings of a 7 letter string with a minimum of length 3. Then compare all available combination to every word in the dictionary to find all the valid words. I'm using a recursive method. Here's the code.

// Gets all the permutations of a string.
void permuteString(String beginningString, String endingString) {
    if (endingString.length() <= 1){
        if((Arrays.binarySearch(mDictionary, beginningString.toLowerCase() +   endingString.toLowerCase())) >= 0){
            mWordSet.add(beginningString + endingString);
        }
    }
    else
        for (int i = 0; i < endingString.length(); i++) {
            String newString = endingString.substring(0, i) + endingString.substring(i + 1);
            permuteString(beginningString + endingString.charAt(i), newString);
      }
}
// Get the combinations of the sub-strings. Minimum 3 letter combinations
void subStrings(String s){
    String newString = "";
    if(s.length() > 3){
        for(int x = 0; x < s.length(); x++){
            newString = removeCharAt(x, s);
            permuteString("", newString);
            subStrings(newString);
        }
    }
}

The above code runs fine but when I installed it on my Nexus s I realized that it runs a bit too slow. It takes a few seconds to complete. About 3 or 4 seconds which is unacceptable. Now I've played some word games on my phone and they compute all the combinations of a string instantly which makes me believe that my algorithm is not very efficient and it can be improved. Can anyone help?

---

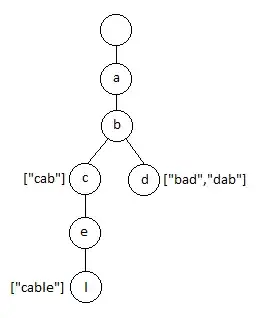
public class TrieNode {
TrieNode a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z;
TrieNode[] children = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z};
private ArrayList<String> words = new ArrayList<String>();

public void addWord(String word){
    words.add(word);
}
public ArrayList<String> getWords(){
    return words;
}
}

---

public class Trie {

static String myWord;
static String myLetters = "afinnrty";
static char[] myChars;
static Sort sort;
static TrieNode myNode = new TrieNode();
static TrieNode currentNode;
static int y = 0;
static ArrayList<String> availableWords = new ArrayList<String>();

public static void main(String[] args) {

    readWords();
    getPermutations();
}
public static void getPermutations(){
    currentNode = myNode;
    for(int x = 0; x < myLetters.length(); x++){
        if(currentNode.children[myLetters.charAt(x) - 'a'] != null){
            //availableWords.addAll(currentNode.getWords());
            currentNode = currentNode.children[myLetters.charAt(x) - 'a'];
            System.out.println(currentNode.getWords() + "" + myLetters.charAt(x));
        }
    }
    //System.out.println(availableWords);
}
public static void readWords(){
    try {
        BufferedReader in = new BufferedReader(new FileReader("c://scrabbledictionary.txt"));
        String str;
        while ((str = in.readLine()) != null) {
            myWord = str;
            myChars = str.toCharArray();
            sort = new Sort(myChars);
            insert(myNode, myChars, 0);
        }
        in.close();
    } catch (IOException e) {
    }
}
public static void insert(TrieNode node, char[] myChars, int x){    
    if(x >= myChars.length){
        node.addWord(myWord);
        //System.out.println(node.getWords()+""+y);
        y++;
        return;
    }
    if(node.children[myChars[x]-'a'] == null){
        insert(node.children[myChars[x]-'a'] = new TrieNode(), myChars, x=x+1);
    }else{
        insert(node.children[myChars[x]-'a'], myChars, x=x+1);
    }
}
}

Answer 1

In your current approach, you're looking up every permutation of each substring. So for "abc", you need to look up "abc", "acb", "bac", "bca", "cab" and "cba". If you wanted to find all permutations of "permutations", your number of lookups is nearly 500,000,000, and that's before you've even looked at its substrings. But we can reduce this to one lookup, regardless of length, by preprocessing the dictionary.

The idea is to put each word in the dictionary into some data structure where each element contains a set of characters, and a list of all words containing (only) those characters. So for example, you could build a binary tree, which would have a node containing the (sorted) character set "abd" and the word list ["bad", "dab"]. Now, if we want to find all permutations of "dba", we sort it to give "abd" and look it up in the tree to retrieve the list.

As Baumann pointed out, tries are well suited to storing this kind of data. The beauty of the trie is that the lookup time depends only on the length of your search string - it is independent of the size of your dictionary. Since you'll be storing quite a lot of words, and most of your search strings will be tiny (the majority will be the 3-character substrings from the lowest level of your recursion), this structure is ideal.

In this case, the paths down your trie would reflect the character sets rather than the words themselves. So if your entire dictionary was ["bad", "dab", "cab", "cable"], your lookup structure would end up looking like this:

There's a bit of a time/space trade-off in the way you implement this. In the simplest (and fastest) approach, each Node contains just the list of words, and an array Node[26] of children. This allows you to locate the child you're after in constant time, just by looking at children[s.charAt(i)-'a'] (where s is your search string and i is your current depth in the trie).

The downside is that most of your children arrays will be mostly empty. If space is an issue, you can use a more compact representation like a linked list, dynamic array, hash table, etc. However, these come at the cost of potentially requiring several memory accesses and comparisons at each node, instead of the simple array access above. But I'd be surprised if the wasted space was more than a few megabytes over your whole dictionary, so the array-based approach is likely your best bet.

With the trie in place, your whole permutation function is replaced with one lookup, bringing the complexity down from O(N! log D) (where D is the size of your dictionary, N the size of your string) to O(N log N) (since you need to sort the characters; the lookup itself is O(N)).

EDIT: I've thrown together an (untested) implementation of this structure: http://pastebin.com/Qfu93E80

Answer 2

  static List<String> permutations(String a) {
    List<String> result=new LinkedList<String>();
    int len = a.length();
    if (len<=1){
      result.add(a);
    }else{
      for (int i=0;i<len; i++){
        for (String it:permutations(a.substring(0, i)+a.substring(i+1))){
          result.add(a.charAt(i)+it);
        }
      }
    }
    return result;
  }

Answer 3

I don't think adding all permutations is necessary. You can simply encapsulate the string into a PermutationString:

public class PermutationString {

    private final String innerString;

    public PermutationString(String innerString) {
        this.innerString = innerString;
    }

    @Override
    public int hashCode() {
        int hash = 0x00;
        String s1 = this.innerString;
        for(int i = 0; i < s1.length(); i++) {
            hash += s1.charAt(i);
        }
        return hash;
    }

    @Override
    public boolean equals(Object obj) {
        if (obj == null) {
            return false;
        }
        if (getClass() != obj.getClass()) {
            return false;
        }
        final PermutationString other = (PermutationString) obj;
        int nChars = 26;
        int[] chars = new int[nChars];
        String s1 = this.innerString;
        String s2 = other.innerString;
        if(s1.length() != s2.length()) {
            return false;
        }
        for(int i = 0; i < s1.length(); i++) {
            chars[s1.charAt(i)-'a']++;
        }
        for(int i = 0; i < s2.length(); i++) {
            chars[s2.charAt(i)-'a']--;
        }
        for(int i = 0; i < nChars; i++) {
            if(chars[i] != 0x00) {
                return false;
            }
        }
        return true;
    }

}

A PermutationString is a string, but where two PermutationStrings are equal if they have the same frequency of characters. Thus new PermutationString("bad").equals(new PermutationString("dab")). This also holds for the .hashCode(): if the strings are permutations of each other, they will generate the same .hashCode().

Now you can simply a HashMap<PermutationString,ArrayList<String>> as follows:

HashMap<PermutationString,ArrayList<String>> hm = new HashMap<PermutationString,ArrayList<String>>();
String[] dictionary = new String[] {"foo","bar","oof"};
ArrayList<String> items;
for(String s : dictionary) {
    PermutationString ps = new PermutationString(s);
    if(hm.containsKey(ps)) {
        items = hm.get(ps);
        items.add(s);
    } else {
        items = new ArrayList<String>();
        items.add(s);
        hm.put(ps,items);
    }
}

So now we iterate over all possible words in the dictionary, construct a PermutationString as key, and if the key already exists (that means that there is already a word with the same character frequencies), we simply add our own word to it. Otherwise, we add a new ArrayList<String> with the single word.

Now that we have filled up the hm with all permutations (but not that much keys), you can query:

hm.get(new PermutationString("ofo"));

This will return an ArrayList<String> with "foo" and "oof".

Testcase:

HashMap<PermutationString, ArrayList<String>> hm = new HashMap<PermutationString, ArrayList<String>>();
String[] dictionary = new String[]{"foo", "bar", "oof"};
ArrayList<String> items;
for (String s : dictionary) {
    PermutationString ps = new PermutationString(s);
    if (hm.containsKey(ps)) {
        items = hm.get(ps);
        items.add(s);
    } else {
        items = new ArrayList<String>();
        items.add(s);
        hm.put(ps, items);
    }
}
Assert.assertNull(hm.get(new PermutationString("baa")));
Assert.assertNull(hm.get(new PermutationString("brr")));
Assert.assertNotNull(hm.get(new PermutationString("bar")));
Assert.assertEquals(1,hm.get(new PermutationString("bar")).size());
Assert.assertNotNull(hm.get(new PermutationString("rab")));
Assert.assertEquals(1,hm.get(new PermutationString("rab")).size());
Assert.assertNotNull(hm.get(new PermutationString("foo")));
Assert.assertEquals(2,hm.get(new PermutationString("foo")).size());
Assert.assertNotNull(hm.get(new PermutationString("ofo")));
Assert.assertEquals(2,hm.get(new PermutationString("ofo")).size());
Assert.assertNotNull(hm.get(new PermutationString("oof")));
Assert.assertEquals(2,hm.get(new PermutationString("oof")).size());

Answer 4

See here: How to find list of possible words from a letter matrix [Boggle Solver]

The idea behind the code in the answers is as follows:

• Iterate over each word dictionary.
• Iterate over each letter in the word, adding it to a string and adding the string each time to an array of prefixes.
• When creating string combinations, test to see that they exist in the prefix array before branching any further.

Answer 5

Use a Trie

Instead of testing all N! possibilities, you only follow prefix trees that lead to a result. This will significanlty reduce the amount of strings that you're checking against.

Answer 6

Well, you can extend your dictionary entities with array letters[] where letters[i] stays for times that i-th letter of alphabet used in this word. It'll take some additional memory, not far much than it is used now.

Then, for each word which permutations you want to check, you'll need to count number of distinct letters too and then traverse through dictiory with easy comparison procedure. If for all letters for word from dictionary number of occurrences less or equal than for word we are checking - yes, this word can be represented as permutation of substring, otherwise - no.

Complexity: it'll took O(D * maxLen) for precalculation, and O(max(N, D)) for each query.