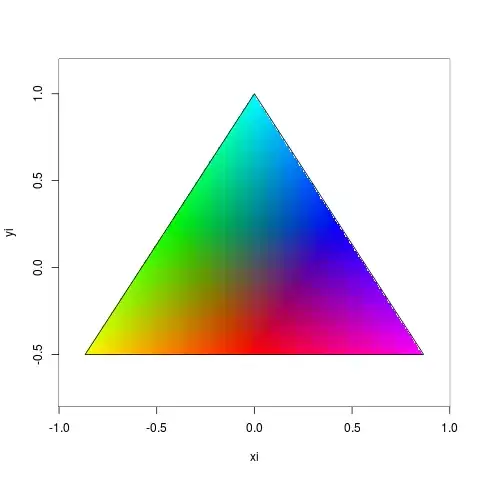
Here is an implementation I worked up for the phonR package... the fillTriangle function is not exported so you have to use the ::: operator to access it. Example shows both pch-based and raster-based approaches.
# set up color scale
colmap <- plotrix::color.scale(x=0:100, cs1=c(0, 180), cs2=100, cs3=c(25, 100),
alpha=1, color.spec='hcl')
# specify triangle vertices and corner colors
vertices <- matrix(c(1, 4, 2, 1, 3, 4, length(colmap), 1, 30), nrow=3,
dimnames=list(NULL, c("x", "y", "z")))
# edit next line to change density / resolution
xseq <- yseq <- seq(0, 5, 0.01)
grid <- expand.grid(x=xseq, y=yseq)
grid$z <- NA
grid.indices <- splancs::inpip(grid, vertices[,1:2], bound=FALSE)
grid$z[grid.indices] <- with(grid[grid.indices,],
phonR:::fillTriangle(x, y, vertices))
# plot it
par(mfrow=c(1,2))
# using pch
with(grid, plot(x, y, col=colmap[round(z)], pch=16))
# overplot original triangle
segments(vertices[,1], vertices[,2], vertices[c(2,3,1),1],
vertices[c(2,3,1),2])
points(vertices[,1:2], pch=21, bg=colmap[vertices[,3]], cex=2)
# using raster
image(xseq, yseq, matrix(grid$z, nrow=length(xseq)), col=colmap)
# overplot original triangle
segments(vertices[,1], vertices[,2], vertices[c(2,3,1),1],
vertices[c(2,3,1),2])
points(vertices[,1:2], pch=21, bg=colmap[vertices[,3]], cex=2)