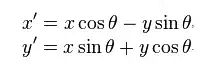Rotating a point about another point (2D)

Question

I'm trying to make a card game where the cards fan out. Right now to display it Im using the Allegro API which has a function:

al_draw_rotated_bitmap(OBJECT_TO_ROTATE,CENTER_X,CENTER_Y,X
        ,Y,DEGREES_TO_ROTATE_IN_RADIANS);

so with this I can make my fan effect easily. The problem is then knowing which card is under the mouse. To do this I thought of doing a polygon collision test. I'm just not sure how to rotate the 4 points on the card to make up the polygon. I basically need to do the same operation as Allegro.

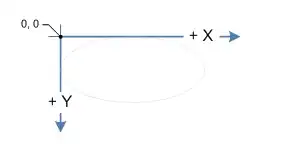
for example, the 4 points of the card are:

card.x

card.y

card.x + card.width

card.y + card.height

I would need a function like:

POINT rotate_point(float cx,float cy,float angle,POINT p)
{
}

Thanks

Answer 1

First subtract the pivot point (cx,cy), then rotate it (counter clock-wise), then add the point again.

Untested:

POINT rotate_point(float cx,float cy,float angle,POINT p)
{
  float s = sin(angle);
  float c = cos(angle);

  // translate point back to origin:
  p.x -= cx;
  p.y -= cy;

  // rotate point
  float xnew = p.x * c - p.y * s;
  float ynew = p.x * s + p.y * c;

  // translate point back:
  p.x = xnew + cx;
  p.y = ynew + cy;
  return p;
}

Answer 2

If you rotate point (px, py) around point (ox, oy) by angle theta you'll get:

p'x = cos(theta) * (px-ox) - sin(theta) * (py-oy) + ox

p'y = sin(theta) * (px-ox) + cos(theta) * (py-oy) + oy

this is an easy way to rotate a point in 2D.

Answer 3

The coordinate system on the screen is left-handed, i.e. the x coordinate increases from left to right and the y coordinate increases from top to bottom. The origin, O(0, 0) is at the upper left corner of the screen.

A clockwise rotation around the origin of a point with coordinates (x, y) is given by the following equations:

where (x', y') are the coordinates of the point after rotation and angle theta, the angle of rotation (needs to be in radians, i.e. multiplied by: PI / 180).

To perform rotation around a point different from the origin O(0,0), let's say point A(a, b) (pivot point). Firstly we translate the point to be rotated, i.e. (x, y) back to the origin, by subtracting the coordinates of the pivot point, (x - a, y - b). Then we perform the rotation and get the new coordinates (x', y') and finally we translate the point back, by adding the coordinates of the pivot point to the new coordinates (x' + a, y' + b).

Following the above description:

a 2D clockwise theta degrees rotation of point (x, y) around point (a, b) is:

Using your function prototype: (x, y) -> (p.x, p.y); (a, b) -> (cx, cy); theta -> angle:

POINT rotate_point(float cx, float cy, float angle, POINT p){

     return POINT(cos(angle) * (p.x - cx) - sin(angle) * (p.y - cy) + cx,
                  sin(angle) * (p.x - cx) + cos(angle) * (p.y - cy) + cy);
}

Answer 4

float s = sin(angle); // angle is in radians
float c = cos(angle); // angle is in radians

For clockwise rotation :

float xnew = p.x * c + p.y * s;
float ynew = -p.x * s + p.y * c;

For counter clockwise rotation :

float xnew = p.x * c - p.y * s;
float ynew = p.x * s + p.y * c;

Answer 5

This is the answer by Nils Pipenbrinck, but implemented in c# fiddle.

https://dotnetfiddle.net/btmjlG

using System;

public class Program
{
    public static void Main()
    {   
        var angle = 180 * Math.PI/180;
        Console.WriteLine(rotate_point(0,0,angle,new Point{X=10, Y=10}).Print());
    }

    static Point rotate_point(double cx, double cy, double angle, Point p)
    {
        double s = Math.Sin(angle);
        double c = Math.Cos(angle);
        // translate point back to origin:
        p.X -= cx;
        p.Y -= cy;
        // rotate point
        double Xnew = p.X * c - p.Y * s;
        double Ynew = p.X * s + p.Y * c;
        // translate point back:
        p.X = Xnew + cx;
        p.Y = Ynew + cy;
        return p;
    }

    class Point
    {
        public double X;
        public double Y;

        public string Print(){
            return $"{X},{Y}";
        }
    }
}

Ps: Apparently I can’t comment, so I’m obligated to post it as an answer ...

Answer 6

I struggled while working MS OCR Read API which returns back angle of rotation in range (-180, 180]. So I have to do an extra step of converting negative angles to positive. I hope someone struggling with point rotation with negative or positive angles can use the following.

def rotate(origin, point, angle):
    """
    Rotate a point counter-clockwise by a given angle around a given origin.
    """
    # Convert negative angles to positive
    angle = normalise_angle(angle)

    # Convert to radians
    angle = math.radians(angle)

    # Convert to radians
    ox, oy = origin
    px, py = point
    
    # Move point 'p' to origin (0,0)
    _px = px - ox
    _py = py - oy
    
    # Rotate the point 'p' 
    qx = (math.cos(angle) * _px) - (math.sin(angle) * _py)
    qy = (math.sin(angle) * _px) + (math.cos(angle) * _py)
    
    # Move point 'p' back to origin (ox, oy)
    qx = ox + qx
    qy = oy + qy
    
    return [qx, qy]


def normalise_angle(angle):
    """ If angle is negative then convert it to positive. """
    if (angle != 0) & (abs(angle) == (angle * -1)):
        angle = 360 + angle
    return angle