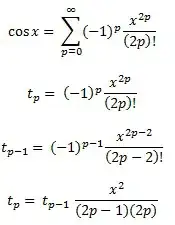How does C compute sin() and other math functions?

Question

I've been poring through .NET disassemblies and the GCC source code, but can't seem to find anywhere the actual implementation of sin() and other math functions... they always seem to be referencing something else.

Can anyone help me find them? I feel like it's unlikely that ALL hardware that C will run on supports trig functions in hardware, so there must be a software algorithm somewhere, right?

---

I'm aware of several ways that functions can be calculated, and have written my own routines to compute functions using taylor series for fun. I'm curious about how real, production languages do it, since all of my implementations are always several orders of magnitude slower, even though I think my algorithms are pretty clever (obviously they're not).

Answer 1

In GNU libm, the implementation of sin is system-dependent. Therefore you can find the implementation, for each platform, somewhere in the appropriate subdirectory of sysdeps.

One directory includes an implementation in C, contributed by IBM. Since October 2011, this is the code that actually runs when you call sin() on a typical x86-64 Linux system. It is apparently faster than the fsin assembly instruction. Source code: sysdeps/ieee754/dbl-64/s_sin.c, look for __sin (double x).

This code is very complex. No one software algorithm is as fast as possible and also accurate over the whole range of x values, so the library implements several different algorithms, and its first job is to look at x and decide which algorithm to use.

• When x is very very close to 0, sin(x) == x is the right answer.

• A bit further out, sin(x) uses the familiar Taylor series. However, this is only accurate near 0, so...

• When the angle is more than about 7°, a different algorithm is used, computing Taylor-series approximations for both sin(x) and cos(x), then using values from a precomputed table to refine the approximation.

• When |x| > 2, none of the above algorithms would work, so the code starts by computing some value closer to 0 that can be fed to sin or cos instead.

• There's yet another branch to deal with x being a NaN or infinity.

This code uses some numerical hacks I've never seen before, though for all I know they might be well-known among floating-point experts. Sometimes a few lines of code would take several paragraphs to explain. For example, these two lines

double t = (x * hpinv + toint);
double xn = t - toint;

are used (sometimes) in reducing x to a value close to 0 that differs from x by a multiple of π/2, specifically xn × π/2. The way this is done without division or branching is rather clever. But there's no comment at all!

---

Older 32-bit versions of GCC/glibc used the fsin instruction, which is surprisingly inaccurate for some inputs. There's a fascinating blog post illustrating this with just 2 lines of code.

fdlibm's implementation of sin in pure C is much simpler than glibc's and is nicely commented. Source code: fdlibm/s_sin.c and fdlibm/k_sin.c

Answer 2

Functions like sine and cosine are implemented in microcode inside microprocessors. Intel chips, for example, have assembly instructions for these. A C compiler will generate code that calls these assembly instructions. (By contrast, a Java compiler will not. Java evaluates trig functions in software rather than hardware, and so it runs much slower.)

Chips do not use Taylor series to compute trig functions, at least not entirely. First of all they use CORDIC, but they may also use a short Taylor series to polish up the result of CORDIC or for special cases such as computing sine with high relative accuracy for very small angles. For more explanation, see this StackOverflow answer.

Answer 3

OK kiddies, time for the pros.... This is one of my biggest complaints with inexperienced software engineers. They come in calculating transcendental functions from scratch (using Taylor's series) as if nobody had ever done these calculations before in their lives. Not true. This is a well defined problem and has been approached thousands of times by very clever software and hardware engineers and has a well defined solution. Basically, most of the transcendental functions use Chebyshev Polynomials to calculate them. As to which polynomials are used depends on the circumstances. First, the bible on this matter is a book called "Computer Approximations" by Hart and Cheney. In that book, you can decide if you have a hardware adder, multiplier, divider, etc, and decide which operations are fastest. e.g. If you had a really fast divider, the fastest way to calculate sine might be P1(x)/P2(x) where P1, P2 are Chebyshev polynomials. Without the fast divider, it might be just P(x), where P has much more terms than P1 or P2....so it'd be slower. So, first step is to determine your hardware and what it can do. Then you choose the appropriate combination of Chebyshev polynomials (is usually of the form cos(ax) = aP(x) for cosine for example, again where P is a Chebyshev polynomial). Then you decide what decimal precision you want. e.g. if you want 7 digits precision, you look that up in the appropriate table in the book I mentioned, and it will give you (for precision = 7.33) a number N = 4 and a polynomial number 3502. N is the order of the polynomial (so it's p4.x^4 + p3.x^3 + p2.x^2 + p1.x + p0), because N=4. Then you look up the actual value of the p4,p3,p2,p1,p0 values in the back of the book under 3502 (they'll be in floating point). Then you implement your algorithm in software in the form: (((p4.x + p3).x + p2).x + p1).x + p0 ....and this is how you'd calculate cosine to 7 decimal places on that hardware.

Note that most hardware implementations of transcendental operations in an FPU usually involve some microcode and operations like this (depends on the hardware). Chebyshev polynomials are used for most transcendentals but not all. e.g. Square root is faster to use a double iteration of Newton raphson method using a lookup table first. Again, that book "Computer Approximations" will tell you that.

If you plan on implmementing these functions, I'd recommend to anyone that they get a copy of that book. It really is the bible for these kinds of algorithms. Note that there are bunches of alternative means for calculating these values like cordics, etc, but these tend to be best for specific algorithms where you only need low precision. To guarantee the precision every time, the chebyshev polynomials are the way to go. Like I said, well defined problem. Has been solved for 50 years now.....and thats how it's done.

Now, that being said, there are techniques whereby the Chebyshev polynomials can be used to get a single precision result with a low degree polynomial (like the example for cosine above). Then, there are other techniques to interpolate between values to increase the accuracy without having to go to a much larger polynomial, such as "Gal's Accurate Tables Method". This latter technique is what the post referring to the ACM literature is referring to. But ultimately, the Chebyshev Polynomials are what are used to get 90% of the way there.

Enjoy.

Answer 4

For sin specifically, using Taylor expansion would give you:

sin(x) := x - x^3/3! + x^5/5! - x^7/7! + ... (1)

you would keep adding terms until either the difference between them is lower than an accepted tolerance level or just for a finite amount of steps (faster, but less precise). An example would be something like:

float sin(float x)
{
  float res=0, pow=x, fact=1;
  for(int i=0; i<5; ++i)
  {
    res+=pow/fact;
    pow*=-1*x*x;
    fact*=(2*(i+1))*(2*(i+1)+1);
  }

  return res;
}

Note: (1) works because of the aproximation sin(x)=x for small angles. For bigger angles you need to calculate more and more terms to get acceptable results. You can use a while argument and continue for a certain accuracy:

double sin (double x){
    int i = 1;
    double cur = x;
    double acc = 1;
    double fact= 1;
    double pow = x;
    while (fabs(acc) > .00000001 &&   i < 100){
        fact *= ((2*i)*(2*i+1));
        pow *= -1 * x*x; 
        acc =  pow / fact;
        cur += acc;
        i++;
    }
    return cur;

}

Answer 5

Concerning trigonometric function like sin(), cos(),tan() there has been no mention, after 5 years, of an important aspect of high quality trig functions: Range reduction.

An early step in any of these functions is to reduce the angle, in radians, to a range of a 2*π interval. But π is irrational so simple reductions like x = remainder(x, 2*M_PI) introduce error as M_PI, or machine pi, is an approximation of π. So, how to do x = remainder(x, 2*π)?

Early libraries used extended precision or crafted programming to give quality results but still over a limited range of double. When a large value was requested like sin(pow(2,30)), the results were meaningless or 0.0 and maybe with an error flag set to something like TLOSS total loss of precision or PLOSS partial loss of precision.

Good range reduction of large values to an interval like -π to π is a challenging problem that rivals the challenges of the basic trig function, like sin(), itself.

A good report is Argument reduction for huge arguments: Good to the last bit (1992). It covers the issue well: discusses the need and how things were on various platforms (SPARC, PC, HP, 30+ other) and provides a solution algorithm the gives quality results for all double from -DBL_MAX to DBL_MAX.

---

If the original arguments are in degrees, yet may be of a large value, use fmod() first for improved precision. A good fmod() will introduce no error and so provide excellent range reduction.

// sin(degrees2radians(x))
sin(degrees2radians(fmod(x, 360.0))); // -360.0 < fmod(x,360) < +360.0

Various trig identities and remquo() offer even more improvement. Sample: sind()

Answer 6

Yes, there are software algorithms for calculating sin too. Basically, calculating these kind of stuff with a digital computer is usually done using numerical methods like approximating the Taylor series representing the function.

Numerical methods can approximate functions to an arbitrary amount of accuracy and since the amount of accuracy you have in a floating number is finite, they suit these tasks pretty well.

Answer 7

Use Taylor series and try to find relation between terms of the series so you don't calculate things again and again

Here is an example for cosinus:

double cosinus(double x, double prec)
{
    double t, s ;
    int p;
    p = 0;
    s = 1.0;
    t = 1.0;
    while(fabs(t/s) > prec)
    {
        p++;
        t = (-t * x * x) / ((2 * p - 1) * (2 * p));
        s += t;
    }
    return s;
}

using this we can get the new term of the sum using the already used one (we avoid the factorial and x^2p)

Answer 8

It is a complex question. Intel-like CPU of the x86 family have a hardware implementation of the sin() function, but it is part of the x87 FPU and not used anymore in 64-bit mode (where SSE2 registers are used instead). In that mode, a software implementation is used.

There are several such implementations out there. One is in fdlibm and is used in Java. As far as I know, the glibc implementation contains parts of fdlibm, and other parts contributed by IBM.

Software implementations of transcendental functions such as sin() typically use approximations by polynomials, often obtained from Taylor series.

Answer 9

Chebyshev polynomials, as mentioned in another answer, are the polynomials where the largest difference between the function and the polynomial is as small as possible. That is an excellent start.

In some cases, the maximum error is not what you are interested in, but the maximum relative error. For example for the sine function, the error near x = 0 should be much smaller than for larger values; you want a small relative error. So you would calculate the Chebyshev polynomial for sin x / x, and multiply that polynomial by x.

Next you have to figure out how to evaluate the polynomial. You want to evaluate it in such a way that the intermediate values are small and therefore rounding errors are small. Otherwise the rounding errors might become a lot larger than errors in the polynomial. And with functions like the sine function, if you are careless then it may be possible that the result that you calculate for sin x is greater than the result for sin y even when x < y. So careful choice of the calculation order and calculation of upper bounds for the rounding error are needed.

For example, sin x = x - x^3/6 + x^5 / 120 - x^7 / 5040... If you calculate naively sin x = x * (1 - x^2/6 + x^4/120 - x^6/5040...), then that function in parentheses is decreasing, and it will happen that if y is the next larger number to x, then sometimes sin y will be smaller than sin x. Instead, calculate sin x = x - x^3 * (1/6 - x^2 / 120 + x^4/5040...) where this cannot happen.

When calculating Chebyshev polynomials, you usually need to round the coefficients to double precision, for example. But while a Chebyshev polynomial is optimal, the Chebyshev polynomial with coefficients rounded to double precision is not the optimal polynomial with double precision coefficients!

For example for sin (x), where you need coefficients for x, x^3, x^5, x^7 etc. you do the following: Calculate the best approximation of sin x with a polynomial (ax + bx^3 + cx^5 + dx^7) with higher than double precision, then round a to double precision, giving A. The difference between a and A would be quite large. Now calculate the best approximation of (sin x - Ax) with a polynomial (b x^3 + cx^5 + dx^7). You get different coefficients, because they adapt to the difference between a and A. Round b to double precision B. Then approximate (sin x - Ax - Bx^3) with a polynomial cx^5 + dx^7 and so on. You will get a polynomial that is almost as good as the original Chebyshev polynomial, but much better than Chebyshev rounded to double precision.

Next you should take into account the rounding errors in the choice of polynomial. You found a polynomial with minimum error in the polynomial ignoring rounding error, but you want to optimise polynomial plus rounding error. Once you have the Chebyshev polynomial, you can calculate bounds for the rounding error. Say f (x) is your function, P (x) is the polynomial, and E (x) is the rounding error. You don't want to optimise | f (x) - P (x) |, you want to optimise | f (x) - P (x) +/- E (x) |. You will get a slightly different polynomial that tries to keep the polynomial errors down where the rounding error is large, and relaxes the polynomial errors a bit where the rounding error is small.

All this will get you easily rounding errors of at most 0.55 times the last bit, where +,-,*,/ have rounding errors of at most 0.50 times the last bit.

Answer 10

The actual implementation of library functions is up to the specific compiler and/or library provider. Whether it's done in hardware or software, whether it's a Taylor expansion or not, etc., will vary.

I realize that's absolutely no help.

Answer 11

There's nothing like hitting the source and seeing how someone has actually done it in a library in common use; let's look at one C library implementation in particular. I chose uLibC.

Here's the sin function:

http://git.uclibc.org/uClibc/tree/libm/s_sin.c

which looks like it handles a few special cases, and then carries out some argument reduction to map the input to the range [-pi/4,pi/4], (splitting the argument into two parts, a big part and a tail) before calling

http://git.uclibc.org/uClibc/tree/libm/k_sin.c

which then operates on those two parts. If there is no tail, an approximate answer is generated using a polynomial of degree 13. If there is a tail, you get a small corrective addition based on the principle that sin(x+y) = sin(x) + sin'(x')y

Answer 12

They are typically implemented in software and will not use the corresponding hardware (that is, aseembly) calls in most cases. However, as Jason pointed out, these are implementation specific.

Note that these software routines are not part of the compiler sources, but will rather be found in the correspoding library such as the clib, or glibc for the GNU compiler. See http://www.gnu.org/software/libc/manual/html_mono/libc.html#Trig-Functions

If you want greater control, you should carefully evaluate what you need exactly. Some of the typical methods are interpolation of look-up tables, the assembly call (which is often slow), or other approximation schemes such as Newton-Raphson for square roots.

Answer 13

If you want an implementation in software, not hardware, the place to look for a definitive answer to this question is Chapter 5 of Numerical Recipes. My copy is in a box, so I can't give details, but the short version (if I remember this right) is that you take tan(theta/2) as your primitive operation and compute the others from there. The computation is done with a series approximation, but it's something that converges much more quickly than a Taylor series.

Sorry I can't rembember more without getting my hand on the book.

Answer 14

Whenever such a function is evaluated, then at some level there is most likely either:

• A table of values which is interpolated (for fast, inaccurate applications - e.g. computer graphics)
• The evaluation of a series that converges to the desired value --- probably not a taylor series, more likely something based on a fancy quadrature like Clenshaw-Curtis.

If there is no hardware support then the compiler probably uses the latter method, emitting only assembler code (with no debug symbols), rather than using a c library --- making it tricky for you to track the actual code down in your debugger.

Answer 15

I'll try to answer for the case of sin() in a C program, compiled with GCC's C compiler on a current x86 processor (let's say a Intel Core 2 Duo).

In the C language the Standard C Library includes common math functions, not included in the language itself (e.g. pow, sin and cos for power, sine, and cosine respectively). The headers of which are included in math.h.

Now on a GNU/Linux system, these libraries functions are provided by glibc (GNU libc or GNU C Library). But the GCC compiler wants you to link to the math library (libm.so) using the -lm compiler flag to enable usage of these math functions. I'm not sure why it isn't part of the standard C library. These would be a software version of the floating point functions, or "soft-float".

Aside: The reason for having the math functions separate is historic, and was merely intended to reduce the size of executable programs in very old Unix systems, possibly before shared libraries were available, as far as I know.

Now the compiler may optimize the standard C library function sin() (provided by libm.so) to be replaced with an call to a native instruction to your CPU/FPU's built-in sin() function, which exists as an FPU instruction (FSIN for x86/x87) on newer processors like the Core 2 series (this is correct pretty much as far back as the i486DX). This would depend on optimization flags passed to the gcc compiler. If the compiler was told to write code that would execute on any i386 or newer processor, it would not make such an optimization. The -mcpu=486 flag would inform the compiler that it was safe to make such an optimization.

Now if the program executed the software version of the sin() function, it would do so based on a CORDIC (COordinate Rotation DIgital Computer) or BKM algorithm, or more likely a table or power-series calculation which is commonly used now to calculate such transcendental functions. [Src: http://en.wikipedia.org/wiki/Cordic#Application]

Any recent (since 2.9x approx.) version of gcc also offers a built-in version of sin, __builtin_sin() that it will used to replace the standard call to the C library version, as an optimization.

I'm sure that is as clear as mud, but hopefully gives you more information than you were expecting, and lots of jumping off points to learn more yourself.

Answer 16

If you want to look at the actual GNU implementation of those functions in C, check out the latest trunk of glibc. See the GNU C Library.

Answer 17

As many people pointed out, it is implementation dependent. But as far as I understand your question, you were interested in a real software implemetnation of math functions, but just didn't manage to find one. If this is the case then here you are:

• Download glibc source code from http://ftp.gnu.org/gnu/glibc/
• Look at file dosincos.c located in unpacked glibc root\sysdeps\ieee754\dbl-64 folder
• Similarly you can find implementations of the rest of the math library, just look for the file with appropriate name

You may also have a look at the files with the .tbl extension, their contents is nothing more than huge tables of precomputed values of different functions in a binary form. That is why the implementation is so fast: instead of computing all the coefficients of whatever series they use they just do a quick lookup, which is much faster. BTW, they do use Tailor series to calculate sine and cosine.

I hope this helps.

Answer 18

Don't use Taylor series. Chebyshev polynomials are both faster and more accurate, as pointed out by a couple of people above. Here is an implementation (originally from the ZX Spectrum ROM): https://albertveli.wordpress.com/2015/01/10/zx-sine/

Answer 19

Computing sine/cosine/tangent is actually very easy to do through code using the Taylor series. Writing one yourself takes like 5 seconds.

The whole process can be summed up with this equation here:

Here are some routines I wrote for C:

double _pow(double a, double b) {
    double c = 1;
    for (int i=0; i<b; i++)
        c *= a;
    return c;
}

double _fact(double x) {
    double ret = 1;
    for (int i=1; i<=x; i++) 
        ret *= i;
    return ret;
}

double _sin(double x) {
    double y = x;
    double s = -1;
    for (int i=3; i<=100; i+=2) {
        y+=s*(_pow(x,i)/_fact(i));
        s *= -1;
    }  
    return y;
}
double _cos(double x) {
    double y = 1;
    double s = -1;
    for (int i=2; i<=100; i+=2) {
        y+=s*(_pow(x,i)/_fact(i));
        s *= -1;
    }  
    return y;
}
double _tan(double x) {
     return (_sin(x)/_cos(x));  
}

Answer 20

Improved version of code from Blindy's answer

#define EPSILON .0000000000001
// this is smallest effective threshold, at least on my OS (WSL ubuntu 18)
// possibly because factorial part turns 0 at some point
// and it happens faster then series element turns 0;
// validation was made against sin() from <math.h>
double ft_sin(double x)
{
    int k = 2;
    double r = x;
    double acc = 1;
    double den = 1;
    double num = x;

//  precision drops rapidly when x is not close to 0
//  so move x to 0 as close as possible
    while (x > PI)
        x -= PI;
    while (x < -PI)
        x += PI;
    if (x > PI / 2)
        return (ft_sin(PI - x));
    if (x < -PI / 2)
        return (ft_sin(-PI - x));
//  not using fabs for performance reasons
    while (acc > EPSILON || acc < -EPSILON)
    {
        num *= -x * x;
        den *= k * (k + 1);
        acc = num / den;
        r += acc;
        k += 2;
    }
    return (r);
}

Answer 21

The essence of how it does this lies in this excerpt from Applied Numerical Analysis by Gerald Wheatley:

When your software program asks the computer to get a value of or , have you wondered how it can get the values if the most powerful functions it can compute are polynomials? It doesnt look these up in tables and interpolate! Rather, the computer approximates every function other than polynomials from some polynomial that is tailored to give the values very accurately.

A few points to mention on the above is that some algorithms do infact interpolate from a table, albeit only for the first few iterations. Also note how it mentions that computers utilise approximating polynomials without specifying which type of approximating polynomial. As others in the thread have pointed out, Chebyshev polynomials are more efficient than Taylor polynomials in this case.

Answer 22

if you want sin then

 __asm__ __volatile__("fsin" : "=t"(vsin) : "0"(xrads));

if you want cos then

 __asm__ __volatile__("fcos" : "=t"(vcos) : "0"(xrads));

if you want sqrt then

 __asm__ __volatile__("fsqrt" : "=t"(vsqrt) : "0"(value));

so why use inaccurate code when the machine instructions will do?