[Complete re-edit 18.10.2017]
the geometry storage is on you. Either you store it in some kind of Mesh or you generate it on the fly. I prefer to store it. In form of 2 tables. One holding all the vertexes (no duplicates) and the other holding 6 indexes of used points per each hex you got and some aditional info like spherical position to ease up the post processing.
Now how to generate this:
create hex triangle
the size should be radius of your sphere. do not include the corner hexess and also skip last line of the triangle (on both radial and axial so there is 1 hex gap between neighbor triangles on sphere) as that would overlap when joining out triangle segments.
convert 60deg hexagon triangle to 72deg pie
so simply convert to polar coordiantes (radius,angle), center triangle around 0 deg. Then multiply radius by cos(angle)/cos(30); which will convert triangle into Pie. And then rescale angle with ratio 72/60. That will make our triangle joinable...
copy&rotate triangle to fill 5 segments of pentagon
easy just rotate the points of first triangle and store as new one.
compute z
based on this Hexagonal tilling of hemi-sphere you can convert distance in 2D map into arc-length to limit the distortions as much a s possible.
However when I tried it (example below) the hexagons are a bit distorted so the depth and scaling needs some tweaking. Or post processing latter.
copy the half sphere to form a sphere
simply copy the points/hexes and negate z axis (or rotate by 180 deg if you want to preserve winding).
add equator and all of the missing pentagons and hexes
You should use the coordinates of the neighboring hexes so no more distortion and overlaps are added to the grid. Here preview:
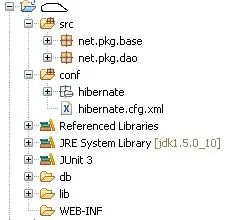
Blue is starting triangle. Darker blue are its copies. Red are pole pentagons. Dark green is the equator, Lighter green are the join lines between triangles. In Yellowish are the missing equator hexagons near Dark Orange pentagons.
Here simple C++ OpenGL example (made from the linked answer in #4):
//$$---- Form CPP ----
//---------------------------------------------------------------------------
#include <vcl.h>
#include <math.h>
#pragma hdrstop
#include "win_main.h"
#include "gl/OpenGL3D_double.cpp"
#include "PolyLine.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TMain *Main;
OpenGLscreen scr;
bool _redraw=true;
double animx= 0.0,danimx=0.0;
double animy= 0.0,danimy=0.0;
//---------------------------------------------------------------------------
PointTab pnt; // (x,y,z)
struct _hexagon
{
int ix[6]; // index of 6 points, last point duplicate for pentagon
int a,b; // spherical coordinate
DWORD col; // color
// inline
_hexagon() {}
_hexagon(_hexagon& a) { *this=a; }
~_hexagon() {}
_hexagon* operator = (const _hexagon *a) { *this=*a; return this; }
//_hexagon* operator = (const _hexagon &a) { ...copy... return this; }
};
List<_hexagon> hex;
//---------------------------------------------------------------------------
// https://stackoverflow.com/a/46787885/2521214
//---------------------------------------------------------------------------
void hex_sphere(int N,double R)
{
const double c=cos(60.0*deg);
const double s=sin(60.0*deg);
const double sy= R/(N+N-2);
const double sz=sy/s;
const double sx=sz*c;
const double sz2=0.5*sz;
const int na=5*(N-2);
const int nb= N;
const int b0= N;
double *q,p[3],ang,len,l,l0,ll;
int i,j,n,a,b,ix;
_hexagon h,*ph;
hex.allocate(na*nb);
hex.num=0;
pnt.reset3D(N*N);
b=0; a=0; ix=0;
// generate triangle hex grid
h.col=0x00804000;
for (b=1;b<N-1;b++) // skip first line b=0
for (a=1;a<b;a++) // skip first and last line
{
p[0]=double(a )*(sx+sz);
p[1]=double(b-(a>>1))*(sy*2.0);
p[2]=0.0;
if (int(a&1)!=0) p[1]-=sy;
ix=pnt.add(p[0]+sz2+sx,p[1] ,p[2]); h.ix[0]=ix; // 2 1
ix=pnt.add(p[0]+sz2 ,p[1]+sy,p[2]); h.ix[1]=ix; // 3 0
ix=pnt.add(p[0]-sz2 ,p[1]+sy,p[2]); h.ix[2]=ix; // 4 5
ix=pnt.add(p[0]-sz2-sx,p[1] ,p[2]); h.ix[3]=ix;
ix=pnt.add(p[0]-sz2 ,p[1]-sy,p[2]); h.ix[4]=ix;
ix=pnt.add(p[0]+sz2 ,p[1]-sy,p[2]); h.ix[5]=ix;
h.a=a;
h.b=N-1-b;
hex.add(h);
} n=hex.num; // remember number of hexs for the first triangle
// distort points to match area
for (ix=0;ix<pnt.nn;ix+=3)
{
// point pointer
q=pnt.pnt.dat+ix;
// convert to polar coordinates
ang=atan2(q[1],q[0]);
len=vector_len(q);
// match area of pentagon (72deg) triangle as we got hexagon (60deg) triangle
ang-=60.0*deg; // rotate so center of generated triangle is angle 0deg
while (ang>+60.0*deg) ang-=pi2;
while (ang<-60.0*deg) ang+=pi2;
len*=cos(ang)/cos(30.0*deg); // scale radius so triangle converts to pie
ang*=72.0/60.0; // scale up angle so rotated triangles merge
// convert back to cartesian
q[0]=len*cos(ang);
q[1]=len*sin(ang);
}
// copy and rotate the triangle to cover pentagon
h.col=0x00404000;
for (ang=72.0*deg,a=1;a<5;a++,ang+=72.0*deg)
for (ph=hex.dat,i=0;i<n;i++,ph++)
{
for (j=0;j<6;j++)
{
vector_copy(p,pnt.pnt.dat+ph->ix[j]);
rotate2d(-ang,p[0],p[1]);
h.ix[j]=pnt.add(p[0],p[1],p[2]);
}
h.a=ph->a+(a*(N-2));
h.b=ph->b;
hex.add(h);
}
// compute z
for (q=pnt.pnt.dat,ix=0;ix<pnt.nn;ix+=pnt.dn,q+=pnt.dn)
{
q[2]=0.0;
ang=vector_len(q)*0.5*pi/R;
q[2]=R*cos(ang);
ll=fabs(R*sin(ang)/sqrt((q[0]*q[0])+(q[1]*q[1])));
q[0]*=ll;
q[1]*=ll;
}
// copy and mirror the other half-sphere
n=hex.num;
for (ph=hex.dat,i=0;i<n;i++,ph++)
{
for (j=0;j<6;j++)
{
vector_copy(p,pnt.pnt.dat+ph->ix[j]);
p[2]=-p[2];
h.ix[j]=pnt.add(p[0],p[1],p[2]);
}
h.a= ph->a;
h.b=-ph->b;
hex.add(h);
}
// create index search table
int i0,i1,j0,j1,a0,a1,ii[5];
int **ab=new int*[na];
for (a=0;a<na;a++)
{
ab[a]=new int[nb+nb+1];
for (b=-nb;b<=nb;b++) ab[a][b0+b]=-1;
}
n=hex.num;
for (ph=hex.dat,i=0;i<n;i++,ph++) ab[ph->a][b0+ph->b]=i;
// add join ring
h.col=0x00408000;
for (a=0;a<na;a++)
{
h.a=a;
h.b=0;
a0=a;
a1=a+1; if (a1>=na) a1-=na;
i0=ab[a0][b0+1];
i1=ab[a1][b0+1];
j0=ab[a0][b0-1];
j1=ab[a1][b0-1];
if ((i0>=0)&&(i1>=0))
if ((j0>=0)&&(j1>=0))
{
h.ix[0]=hex[i1].ix[1];
h.ix[1]=hex[i0].ix[0];
h.ix[2]=hex[i0].ix[1];
h.ix[3]=hex[j0].ix[1];
h.ix[4]=hex[j0].ix[0];
h.ix[5]=hex[j1].ix[1];
hex.add(h);
ab[h.a][b0+h.b]=hex.num-1;
}
}
// add 2x5 join lines
h.col=0x00008040;
for (a=0;a<na;a+=N-2)
for (b=1;b<N-3;b++)
{
// +b hemisphere
h.a= a;
h.b=+b;
a0=a-b; if (a0< 0) a0+=na; i0=ab[a0][b0+b+0];
a0--; if (a0< 0) a0+=na; i1=ab[a0][b0+b+1];
a1=a+1; if (a1>=na) a1-=na; j0=ab[a1][b0+b+0];
j1=ab[a1][b0+b+1];
if ((i0>=0)&&(i1>=0))
if ((j0>=0)&&(j1>=0))
{
h.ix[0]=hex[i0].ix[5];
h.ix[1]=hex[i0].ix[4];
h.ix[2]=hex[i1].ix[5];
h.ix[3]=hex[j1].ix[3];
h.ix[4]=hex[j0].ix[4];
h.ix[5]=hex[j0].ix[3];
hex.add(h);
}
// -b hemisphere
h.a= a;
h.b=-b;
a0=a-b; if (a0< 0) a0+=na; i0=ab[a0][b0-b+0];
a0--; if (a0< 0) a0+=na; i1=ab[a0][b0-b-1];
a1=a+1; if (a1>=na) a1-=na; j0=ab[a1][b0-b+0];
j1=ab[a1][b0-b-1];
if ((i0>=0)&&(i1>=0))
if ((j0>=0)&&(j1>=0))
{
h.ix[0]=hex[i0].ix[5];
h.ix[1]=hex[i0].ix[4];
h.ix[2]=hex[i1].ix[5];
h.ix[3]=hex[j1].ix[3];
h.ix[4]=hex[j0].ix[4];
h.ix[5]=hex[j0].ix[3];
hex.add(h);
}
}
// add pentagons at poles
_hexagon h0,h1;
h0.col=0x00000080;
h0.a=0; h0.b=N-1; h1=h0; h1.b=-h1.b;
p[2]=sqrt((R*R)-(sz*sz));
for (ang=0.0,a=0;a<5;a++,ang+=72.0*deg)
{
p[0]=2.0*sz*cos(ang);
p[1]=2.0*sz*sin(ang);
h0.ix[a]=pnt.add(p[0],p[1],+p[2]);
h1.ix[a]=pnt.add(p[0],p[1],-p[2]);
}
h0.ix[5]=h0.ix[4]; hex.add(h0);
h1.ix[5]=h1.ix[4]; hex.add(h1);
// add 5 missing hexagons at poles
h.col=0x00600060;
for (ph=&h0,b=N-3,h.b=N-2,i=0;i<2;i++,b=-b,ph=&h1,h.b=-h.b)
{
a = 1; if (a>=na) a-=na; ii[0]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[1]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[2]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[3]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[4]=ab[a][b0+b];
for (j=0;j<5;j++)
{
h.a=((4+j)%5)*(N-2)+1;
h.ix[0]=ph->ix[ (5-j)%5 ];
h.ix[1]=ph->ix[ (6-j)%5 ];
h.ix[2]=hex[ii[(j+4)%5]].ix[4];
h.ix[3]=hex[ii[(j+4)%5]].ix[5];
h.ix[4]=hex[ii[ j ]].ix[3];
h.ix[5]=hex[ii[ j ]].ix[4];
hex.add(h);
}
}
// add 2*5 pentagons and 2*5 missing hexagons at equator
h0.a=0; h0.b=N-1; h1=h0; h1.b=-h1.b;
for (ang=36.0*deg,a=0;a<na;a+=N-2,ang-=72.0*deg)
{
p[0]=R*cos(ang);
p[1]=R*sin(ang);
p[2]=sz;
i0=pnt.add(p[0],p[1],+p[2]);
i1=pnt.add(p[0],p[1],-p[2]);
a0=a-1;if (a0< 0) a0+=na;
a1=a+1;if (a1>=na) a1-=na;
ii[0]=ab[a0][b0-1]; ii[2]=ab[a1][b0-1];
ii[1]=ab[a0][b0+1]; ii[3]=ab[a1][b0+1];
// hexagons
h.col=0x00008080;
h.a=a; h.b=0;
h.ix[0]=hex[ii[0]].ix[0];
h.ix[1]=hex[ii[0]].ix[1];
h.ix[2]=hex[ii[1]].ix[1];
h.ix[3]=hex[ii[1]].ix[0];
h.ix[4]=i0;
h.ix[5]=i1;
hex.add(h);
h.a=a; h.b=0;
h.ix[0]=hex[ii[2]].ix[2];
h.ix[1]=hex[ii[2]].ix[1];
h.ix[2]=hex[ii[3]].ix[1];
h.ix[3]=hex[ii[3]].ix[2];
h.ix[4]=i0;
h.ix[5]=i1;
hex.add(h);
// pentagons
h.col=0x000040A0;
h.a=a; h.b=0;
h.ix[0]=hex[ii[0]].ix[0];
h.ix[1]=hex[ii[0]].ix[5];
h.ix[2]=hex[ii[2]].ix[3];
h.ix[3]=hex[ii[2]].ix[2];
h.ix[4]=i1;
h.ix[5]=i1;
hex.add(h);
h.a=a; h.b=0;
h.ix[0]=hex[ii[1]].ix[0];
h.ix[1]=hex[ii[1]].ix[5];
h.ix[2]=hex[ii[3]].ix[3];
h.ix[3]=hex[ii[3]].ix[2];
h.ix[4]=i0;
h.ix[5]=i0;
hex.add(h);
}
// release index search table
for (a=0;a<na;a++) delete[] ab[a];
delete[] ab;
}
//---------------------------------------------------------------------------
void hex_draw(GLuint style) // draw hex
{
int i,j;
_hexagon *h;
for (h=hex.dat,i=0;i<hex.num;i++,h++)
{
if (style==GL_POLYGON) glColor4ubv((BYTE*)&h->col);
glBegin(style);
for (j=0;j<6;j++) glVertex3dv(pnt.pnt.dat+h->ix[j]);
glEnd();
}
if (0)
if (style==GL_POLYGON)
{
scr.text_init_pixel(0.1,-0.2);
glColor3f(1.0,1.0,1.0);
for (h=hex.dat,i=0;i<hex.num;i++,h++)
if (abs(h->b)<2)
{
double p[3];
vector_ld(p,0.0,0.0,0.0);
for (j=0;j<6;j++)
vector_add(p,p,pnt.pnt.dat+h->ix[j]);
vector_mul(p,p,1.0/6.0);
scr.text(p[0],p[1],p[2],AnsiString().sprintf("%i,%i",h->a,h->b));
}
scr.text_exit_pixel();
}
}
//---------------------------------------------------------------------------
void TMain::draw()
{
scr.cls();
int x,y;
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0,0.0,-5.0);
glRotated(animx,1.0,0.0,0.0);
glRotated(animy,0.0,1.0,0.0);
hex_draw(GL_POLYGON);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0,0.0,-5.0+0.01);
glRotated(animx,1.0,0.0,0.0);
glRotated(animy,0.0,1.0,0.0);
glColor3f(1.0,1.0,1.0);
glLineWidth(2);
hex_draw(GL_LINE_LOOP);
glCirclexy(0.0,0.0,0.0,1.5);
glLineWidth(1);
scr.exe();
scr.rfs();
}
//---------------------------------------------------------------------------
__fastcall TMain::TMain(TComponent* Owner) : TForm(Owner)
{
scr.init(this);
hex_sphere(10,1.5);
_redraw=true;
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormDestroy(TObject *Sender)
{
scr.exit();
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormPaint(TObject *Sender)
{
_redraw=true;
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormResize(TObject *Sender)
{
scr.resize();
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(60,float(scr.xs)/float(scr.ys),0.1,100.0);
_redraw=true;
}
//-----------------------------------------------------------------------
void __fastcall TMain::Timer1Timer(TObject *Sender)
{
animx+=danimx; if (animx>=360.0) animx-=360.0; _redraw=true;
animy+=danimy; if (animy>=360.0) animy-=360.0; _redraw=true;
if (_redraw) { draw(); _redraw=false; }
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormKeyDown(TObject *Sender, WORD &Key, TShiftState Shift)
{
Caption=Key;
if (Key==40){ animx+=2.0; _redraw=true; }
if (Key==38){ animx-=2.0; _redraw=true; }
if (Key==39){ animy+=2.0; _redraw=true; }
if (Key==37){ animy-=2.0; _redraw=true; }
}
//---------------------------------------------------------------------------
I know it is a bit of a index mess and also winding rule is not guaranteed as I was too lazy to made uniform indexing. Beware the a indexes of each hex are not linear and if you want to use them to map to 2D map you would need to recompute it using atan2 on x,y of its center point position.
Here previews:

Still some distortions are present. They are caused by fact that we using 5 triangles to connect at equator (so connection is guaranteed). That means the circumference is 5*R instead of 6.28*R. How ever this can be still improved by a field simulation. Just take all the points and add retractive forces based on their distance and bound to sphere surface. Run simulation and when the oscillations lower below threshold you got your sphere grid ...
Another option would be find out some equation to remap the grid points (similarly what I done for triangle to pie conversion) that would have better results.