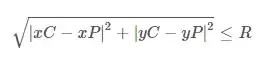Equation for testing if a point is inside a circle

Question

If you have a circle with center (center_x, center_y) and radius radius, how do you test if a given point with coordinates (x, y) is inside the circle?

Answer 1

In general, x and y must satisfy (x - center_x)² + (y - center_y)² < radius².

Please note that points that satisfy the above equation with < replaced by == are considered the points on the circle, and the points that satisfy the above equation with < replaced by > are considered the outside the circle.

Answer 2

Mathematically, Pythagoras is probably a simple method as many have already mentioned.

(x-center_x)^2 + (y - center_y)^2 < radius^2

Computationally, there are quicker ways. Define:

dx = abs(x-center_x)
dy = abs(y-center_y)
R = radius

If a point is more likely to be outside this circle then imagine a square drawn around it such that it's sides are tangents to this circle:

if dx>R then 
    return false.
if dy>R then 
    return false.

Now imagine a square diamond drawn inside this circle such that it's vertices touch this circle:

if dx + dy <= R then 
    return true.

Now we have covered most of our space and only a small area of this circle remains in between our square and diamond to be tested. Here we revert to Pythagoras as above.

if dx^2 + dy^2 <= R^2 then 
    return true
else 
    return false.

If a point is more likely to be inside this circle then reverse order of first 3 steps:

if dx + dy <= R then 
    return true.
if dx > R then 
    return false.
if dy > R 
    then return false.
if dx^2 + dy^2 <= R^2 then 
    return true
else
    return false.

---

Alternate methods imagine a square inside this circle instead of a diamond but this requires slightly more tests and calculations with no computational advantage (inner square and diamonds have identical areas):

k = R/sqrt(2)
if dx <= k and dy <= k then 
    return true.

Update:

For those interested in performance I implemented this method in c, and compiled with -O3.

I obtained execution times by time ./a.out

I implemented this method, a normal method and a dummy method to determine timing overhead.

Normal: 21.3s This: 19.1s Overhead: 16.5s

So, it seems this method is more efficient in this implementation.

// compile gcc -O3 <filename>.c
// run: time ./a.out

#include <stdio.h>
#include <stdlib.h>

#define TRUE  (0==0)
#define FALSE (0==1)

#define ABS(x) (((x)<0)?(0-(x)):(x))

int xo, yo, R;

int inline inCircle( int x, int y ){  // 19.1, 19.1, 19.1
  int dx = ABS(x-xo);
  if (    dx >  R ) return FALSE;
  int dy = ABS(y-yo);
  if (    dy >  R ) return FALSE;
  if ( dx+dy <= R ) return TRUE;
  return ( dx*dx + dy*dy <= R*R );
}

int inline inCircleN( int x, int y ){  // 21.3, 21.1, 21.5
  int dx = ABS(x-xo);
  int dy = ABS(y-yo);
  return ( dx*dx + dy*dy <= R*R );
}

int inline dummy( int x, int y ){  // 16.6, 16.5, 16.4
  int dx = ABS(x-xo);
  int dy = ABS(y-yo);
  return FALSE;
}

#define N 1000000000

int main(){
  int x, y;
  xo = rand()%1000; yo = rand()%1000; R = 1;
  int n = 0;
  int c;
  for (c=0; c<N; c++){
    x = rand()%1000; y = rand()%1000;
//    if ( inCircle(x,y)  ){
    if ( inCircleN(x,y) ){
//    if ( dummy(x,y) ){
      n++;
    }
  }
  printf( "%d of %d inside circle\n", n, N);
}

Answer 3

You can use Pythagoras to measure the distance between your point and the centre and see if it's lower than the radius:

def in_circle(center_x, center_y, radius, x, y):
    dist = math.sqrt((center_x - x) ** 2 + (center_y - y) ** 2)
    return dist <= radius

EDIT (hat tip to Paul)

In practice, squaring is often much cheaper than taking the square root and since we're only interested in an ordering, we can of course forego taking the square root:

def in_circle(center_x, center_y, radius, x, y):
    square_dist = (center_x - x) ** 2 + (center_y - y) ** 2
    return square_dist <= radius ** 2

Also, Jason noted that <= should be replaced by < and depending on usage this may actually make sense even though I believe that it's not true in the strict mathematical sense. I stand corrected.

Answer 4

boolean isInRectangle(double centerX, double centerY, double radius, 
    double x, double y)
{
        return x >= centerX - radius && x <= centerX + radius && 
            y >= centerY - radius && y <= centerY + radius;
}    

//test if coordinate (x, y) is within a radius from coordinate (center_x, center_y)
public boolean isPointInCircle(double centerX, double centerY, 
    double radius, double x, double y)
{
    if(isInRectangle(centerX, centerY, radius, x, y))
    {
        double dx = centerX - x;
        double dy = centerY - y;
        dx *= dx;
        dy *= dy;
        double distanceSquared = dx + dy;
        double radiusSquared = radius * radius;
        return distanceSquared <= radiusSquared;
    }
    return false;
}

This is more efficient, and readable. It avoids the costly square root operation. I also added a check to determine if the point is within the bounding rectangle of the circle.

The rectangle check is unnecessary except with many points or many circles. If most points are inside circles, the bounding rectangle check will actually make things slower!

As always, be sure to consider your use case.

Answer 5

You should check whether the distance from the center of the circle to the point is smaller than the radius

using Python

if (x-center_x)**2 + (y-center_y)**2 <= radius**2:
    # inside circle

Answer 6

Find the distance between the center of the circle and the points given. If the distance between them is less than the radius then the point is inside the circle. if the distance between them is equal to the radius of the circle then the point is on the circumference of the circle. if the distance is greater than the radius then the point is outside the circle.

int d = r^2 - ((center_x-x)^2 + (center_y-y)^2);

if(d>0)
  print("inside");
else if(d==0)
  print("on the circumference");
else
  print("outside");

Answer 7

Calculate the Distance

D = Math.Sqrt(Math.Pow(center_x - x, 2) + Math.Pow(center_y - y, 2))
return D <= radius

that's in C#...convert for use in python...

Answer 8

As said above -- use Euclidean distance.

from math import hypot

def in_radius(c_x, c_y, r, x, y):
    return math.hypot(c_x-x, c_y-y) <= r

Answer 9

The equation below is a expression that tests if a point is within a given circle where xP & yP are the coordinates of the point, xC & yC are the coordinates of the center of the circle and R is the radius of that given circle.

If the above expression is true then the point is within the circle.

Below is a sample implementation in C#:

    public static bool IsWithinCircle(PointF pC, Point pP, Single fRadius){
        return Distance(pC, pP) <= fRadius;
    }

    public static Single Distance(PointF p1, PointF p2){
        Single dX = p1.X - p2.X;
        Single dY = p1.Y - p2.Y;
        Single multi = dX * dX + dY * dY;
        Single dist = (Single)Math.Round((Single)Math.Sqrt(multi), 3);

        return (Single)dist;
    }

Answer 10

This is the same solution as mentioned by Jason Punyon, but it contains a pseudo-code example and some more details. I saw his answer after writing this, but I didn't want to remove mine.

I think the most easily understandable way is to first calculate the distance between the circle's center and the point. I would use this formula:

d = sqrt((circle_x - x)^2 + (circle_y - y)^2)

Then, simply compare the result of that formula, the distance (d), with the radius. If the distance (d) is less than or equal to the radius (r), the point is inside the circle (on the edge of the circle if d and r are equal).

Here is a pseudo-code example which can easily be converted to any programming language:

function is_in_circle(circle_x, circle_y, r, x, y)
{
    d = sqrt((circle_x - x)^2 + (circle_y - y)^2);
    return d <= r;
}

Where circle_x and circle_y is the center coordinates of the circle, r is the radius of the circle, and x and y is the coordinates of the point.

Answer 11

My answer in C# as a complete cut & paste (not optimized) solution:

public static bool PointIsWithinCircle(double circleRadius, double circleCenterPointX, double circleCenterPointY, double pointToCheckX, double pointToCheckY)
{
    return (Math.Pow(pointToCheckX - circleCenterPointX, 2) + Math.Pow(pointToCheckY - circleCenterPointY, 2)) < (Math.Pow(circleRadius, 2));
}

Usage:

if (!PointIsWithinCircle(3, 3, 3, .5, .5)) { }

Answer 12

As stated previously, to show if the point is in the circle we can use the following

if ((x-center_x)^2 + (y - center_y)^2 < radius^2) {
    in.circle <- "True"
} else {
    in.circle <- "False"
}

To represent it graphically we can use:

plot(x, y, asp = 1, xlim = c(-1, 1), ylim = c(-1, 1), col = ifelse((x-center_x)^2 + (y - center_y)^2 < radius^2,'green','red'))
draw.circle(0, 0, 1, nv = 1000, border = NULL, col = NA, lty = 1, lwd = 1)

Answer 13

Moving into the world of 3D if you want to check if a 3D point is in a Unit Sphere you end up doing something similar. All that is needed to work in 2D is to use 2D vector operations.

    public static bool Intersects(Vector3 point, Vector3 center, float radius)
    {
        Vector3 displacementToCenter = point - center;

        float radiusSqr = radius * radius;

        bool intersects = displacementToCenter.magnitude < radiusSqr;

        return intersects;
    }

Answer 14

iOS 15, Accepted Answer written in Swift 5.5

func isInRectangle(center: CGPoint, radius: Double, point: CGPoint) -> Bool
{
    return point.x >= center.x - radius && point.x <= center.x + radius &&
    point.y >= center.y - radius && point.y <= center.y + radius
}

//test if coordinate (x, y) is within a radius from coordinate (center_x, center_y)
func isPointInCircle(center: CGPoint,
                     radius:Double, point: CGPoint) -> Bool
{
    if(isInRectangle(center: center, radius: radius, point: point))
    {
        var dx:Double = center.x - point.x
        var dy:Double = center.y - point.y
        dx *= dx
        dy *= dy
        let distanceSquared:Double = dx + dy
        let radiusSquared:Double = radius * radius
        return distanceSquared <= radiusSquared
    }
    return false
}

Answer 15

I used the code below for beginners like me :).

public class incirkel {

public static void main(String[] args) {
    int x; 
    int y; 
    int middelx; 
    int middely; 
    int straal; {

// Adjust the coordinates of x and y 
x = -1;
y = -2;

// Adjust the coordinates of the circle
middelx = 9; 
middely = 9;
straal =  10;

{
    //When x,y is within the circle the message below will be printed
    if ((((middelx - x) * (middelx - x)) 
                    + ((middely - y) * (middely - y))) 
                    < (straal * straal)) {
                        System.out.println("coordinaten x,y vallen binnen cirkel");
    //When x,y is NOT within the circle the error message below will be printed
    } else {
        System.err.println("x,y coordinaten vallen helaas buiten de cirkel");
    } 
}



    }
}}

Answer 16

Here is the simple java code for solving this problem:

and the math behind it : https://math.stackexchange.com/questions/198764/how-to-know-if-a-point-is-inside-a-circle

boolean insideCircle(int[] point, int[] center, int radius) {
    return (float)Math.sqrt((int)Math.pow(point[0]-center[0],2)+(int)Math.pow(point[1]-center[1],2)) <= radius;
}

Answer 17

PHP

if ((($x - $center_x) ** 2 + ($y - $center_y) ** 2) <=  $radius **2) {
    return true; // Inside
} else {
    return false; // Outside
}