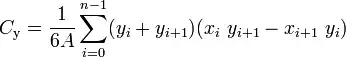Center of gravity of a polygon

Question

I am trying to write a PHP function that will calculate the center of gravity of a polygon.

I've looked at the other similar questions but I can't seem to find a solution to this.

My problem is that I need to be able to calculate the center of gravity for both regular and irregular polygons and even self intersecting polygons.

Is that possible?

I've also read that: http://paulbourke.net/geometry/polyarea/ But this is restricted to non self intersecting polygons.

How can I do this? Can you point me to the right direction?

1) Take a screenshot. 2) Print it out. 3) Cut out the polygon with scissors. 4) Put onto some scales. 5) ???. 6) Profit. — Greg, Mar 11 '11 at 10:17
If you could split self-intersecting polygons into several non-self-intersecting polygons, I guess computing the center of gravity of those polygons would be easy then... — Vincent Mimoun-Prat, Mar 11 '11 at 10:18
@Greg: 5) is "pierce a very small hole, suspend the polygon from a pin through the hole, allow it to hang freely, and draw a vertical line through the hole. Pierce a second hole not on the first line, repeat, and the point of intersection is the centre of mass". There is a small error though for the mass (re)moved by the first hole, when you hang from the second hole, so you might want to use two separate copies of the polygon, or figure out a way to hang the polygon without damaging it. And you may not need to print it, you could simulate in your favourite physics engine ;-) — Steve Jessop, Mar 11 '11 at 10:36

score 47 · Accepted Answer · edited Aug 04 '21 at 01:48

47

The center of gravity (also known as "center of mass" or "centroid" can be calculated with the following formula:

X = SUM[(Xi + Xi+1) * (Xi * Yi+1 - Xi+1 * Yi)] / 6 / A
Y = SUM[(Yi + Yi+1) * (Xi * Yi+1 - Xi+1 * Yi)] / 6 / A

Extracted from Wikipedia: The centroid of a non-self-intersecting closed polygon defined by n vertices (x0,y0), (x1,y1), ..., (xn−1,yn−1) is the point (Cx, Cy), where
X coordinate of the center
Y coordinate of the center
and where A is the polygon's signed area,
Area formula

Example using VBasic:

' Find the polygon's centroid.
Public Sub FindCentroid(ByRef X As Single, ByRef Y As _
    Single)
Dim pt As Integer
Dim second_factor As Single
Dim polygon_area As Single

    ' Add the first point at the end of the array.
    ReDim Preserve m_Points(1 To m_NumPoints + 1)
    m_Points(m_NumPoints + 1) = m_Points(1)

    ' Find the centroid.
    X = 0
    Y = 0
    For pt = 1 To m_NumPoints
        second_factor = _
            m_Points(pt).X * m_Points(pt + 1).Y - _
            m_Points(pt + 1).X * m_Points(pt).Y
        X = X + (m_Points(pt).X + m_Points(pt + 1).X) * _
            second_factor
        Y = Y + (m_Points(pt).Y + m_Points(pt + 1).Y) * _
            second_factor
    Next pt

    ' Divide by 6 times the polygon's area.
    polygon_area = PolygonArea
    X = X / 6 / polygon_area
    Y = Y / 6 / polygon_area

    ' If the values are negative, the polygon is
    ' oriented counterclockwise. Reverse the signs.
    If X < 0 Then
        X = -X
        Y = -Y
    End If
End Sub

For more info check this website or Wikipedia.

Hope it helps.

Regards!

edited Aug 04 '21 at 01:48

Paul Wheeler

18,988
3
28
41

answered Mar 11 '11 at 10:27

redent84

18,901
4
62
85

who said Green formula was useless for computer science :) – Alexandre C. Mar 11 '11 at 10:32
1

Dude thanks for the reply but thats the website that I was looking at! The link is in the original post :) I need a formula that will work for self intersecting polygons!!! – mixkat Mar 11 '11 at 10:33
3

@mixkat For a intersecting polygon you have to use the _integral formula_ as described in the wikipedia article. Or decompose the polygon into non-intersecting polygons and use the method described above. – redent84 Mar 11 '11 at 10:40
This is an incorrect answer - center of gravity is not same as centroid of polygon - when points cannot form a convex shape, you cannot use it at all, as there are more than one polygons that can be formed from such points. – Ωmega Jul 19 '12 at 17:07
2

If a physical object has uniform density, then its center of mass is the same as the centroid of its shape. The requirement for the formula described above is 'a non-self-intersecting closed polygon', so the vertexes of the polygon will form only one non-self-intersecting closed polygon. – redent84 Jul 22 '12 at 15:44
You can try your code [here](http://www.spoj.com/problems/STONE/) against verified data and compare its effectiveness to other submitters. – kuszi Sep 08 '15 at 09:21
That is pretty strange function for calculating center of gravity (not the formula, but the code). I'd expect function that takes an array of PointF and returns single PointF. Instead, there are variables which appear in the middle of the code without explanation. I believe here is the same function modified to respect that: http://www.vb-helper.com/howto_net_polygon_centroid.html – Oak_3260548 Jan 10 '19 at 16:28

score 15 · Answer 2 · edited Apr 22 '23 at 09:24

in cold c++ and while assuming that you have a Vec2 struct with x and y properties :

Vec2 findCentroid(const Vec2* pts, size_t nPts){
    Vec2 off = pts[0];
    float twicearea = 0;
    float x = 0;
    float y = 0;
    Vec2 p1, p2;
    float f;
    for (int i = 0, j = nPts - 1; i < nPts; j = i++) {
        p1 = pts[i];
        p2 = pts[j];
        f = (p1.x - off.x) * (p2.y - off.y) - (p2.x - off.x) * (p1.y - off.y);
        twicearea += f;
        x += (p1.x + p2.x - 2 * off.x) * f;
        y += (p1.y + p2.y - 2 * off.y) * f;
    }

    f = twicearea * 3;

    return Vec2(x / f + off.x, y / f + off.y);
}

and in javascript :

function findCentroid(pts, nPts) {
    var off = pts[0];
    var twicearea = 0;
    var x = 0;
    var y = 0;
    var p1,p2;
    var f;
    for (var i = 0, j = nPts - 1; i < nPts; j = i++) {
        p1 = pts[i];
        p2 = pts[j];
        f = (p1.lat - off.lat) * (p2.lng - off.lng) - (p2.lat - off.lat) * (p1.lng - off.lng);
        twicearea += f;
        x += (p1.lat + p2.lat - 2 * off.lat) * f;
        y += (p1.lng + p2.lng - 2 * off.lng) * f;
    }
    f = twicearea * 3;
    return {
    X: x / f + off.lat,
    Y: y / f + off.lng
    };
}

or in good old c and while assuming that you have a Point struct with x and y properties :

Point centroidForPoly(const int numVerts, const Point* verts)
{
    float sum = 0.0f;
    Point vsum = 0;

    for (int i = 0; i<numVerts; i++){
        Point v1 = verts[i];
        Point v2 = verts[(i + 1) % numVerts];
        float cross = v1.x*v2.y - v1.y*v2.x;
        sum += cross;
        vsum = Point(((v1.x + v2.x) * cross) + vsum.x, ((v1.y + v2.y) * cross) + vsum.y);
    }

    float z = 1.0f / (3.0f * sum);
    return Point(vsum.x * z, vsum.y * z);
}

That is the only one that works out of the box. Btw you forgot the offset in the C version :) — Matthieu, Aug 03 '17 at 14:09
I had to add a special case where the polygos size is 1 or if all the points of the polygon are the same point, ex. it's a dot or an empty polygon. in that case, the COG is just the avarage point. otherwise you get a devision by zero because the cross is 0. So if (sum == 0) return pts.average(); — Yomi1984, Apr 08 '21 at 07:22

score 4 · Answer 3 · answered Oct 14 '18 at 17:47

Swift 4, based on the c answer given above

/// Given an array of points, find the "center of gravity" of the points
/// - Parameters:
///     - points: Array of points
/// - Returns:
///     - Point or nil if input points count < 3
static func centerOfPoints(points: [CGPoint]) -> CGPoint? {
    if points.count < 3 {
        return nil
    }

    var sum: CGFloat = 0
    var pSum: CGPoint = .zero

    for i in 0..<points.count {
        let p1 = points[i]
        let p2 = points[(i+1) % points.count]
        let cross = p1.x * p2.y - p1.y * p2.x
        sum += cross
        pSum = CGPoint(x:((p1.x + p2.x) * cross) + pSum.x,
                       y:((p1.y + p2.y) * cross) + pSum.y)
    }

    let z = 1 / (3 * sum)
    return CGPoint(x:pSum.x * z,
                   y:pSum.y * z)
}

score 2 · Answer 4 · answered Oct 25 '17 at 16:24

Since we are all having so much fun implementing this algo in different languages, here is my version I knocked up for Python:

def polygon_centre_area(vertices: Sequence[Sequence[float]]) -> Tuple[Sequence[float], float]:
    x_cent = y_cent = area = 0
    v_local = vertices + [vertices[0]]

    for i in range(len(v_local) - 1):
        factor = v_local[i][0] * v_local[i+1][1] - v_local[i+1][0] * v_local[i][1]
        area += factor
        x_cent += (v_local[i][0] + v_local[i+1][0]) * factor
        y_cent += (v_local[i][1] + v_local[i+1][1]) * factor

    area /= 2.0
    x_cent /= (6 * area)
    y_cent /= (6 * area)

    area = math.fabs(area)

    return ([x_cent, y_cent], area)

Adrian Cid Almaguer · Answer 5 · 2017-08-03T14:13:21.033

In php:

// Find the polygon's centroid.
function getCenter($polygon)
{ 
    $NumPoints = count($polygon);

    if($polygon[$NumPoints-1] == $polygon[0]){
        $NumPoints--;
    }else{
        //Add the first point at the end of the array.
        $polygon[$NumPoints] = $polygon[0];
    }

    // Find the centroid.
    $X = 0;
    $Y = 0;
    For ($pt = 0 ;$pt<= $NumPoints-1;$pt++){
        $factor = $polygon[$pt][0] * $polygon[$pt + 1][1] - $polygon[$pt + 1][0] * $polygon[$pt][1];
        $X += ($polygon[$pt][0] + $polygon[$pt + 1][0]) * $factor;
        $Y += ($polygon[$pt][1] + $polygon[$pt + 1][1]) * $factor;
    }

    // Divide by 6 times the polygon's area.
    $polygon_area = ComputeArea($polygon);
    $X = $X / 6 / $polygon_area;
    $Y = $Y / 6 / $polygon_area;

    return array($X, $Y);
}


function ComputeArea($polygon)
{ 
    $NumPoints = count($polygon);

    if($polygon[$NumPoints-1] == $polygon[0]){
        $NumPoints--;
    }else{
        //Add the first point at the end of the array.
        $polygon[$NumPoints] = $polygon[0];
    }

    $area = 0;

    for ($i = 0; $i < $NumPoints; $i++) {
      $i1 = ($i + 1) % $NumPoints;
      $area += ($polygon[$i][1] + $polygon[$i1][1]) * ($polygon[$i1][0] - $polygon[$i][0]);
    }

    $area /= 2;
    return $area;
}

Read more at:

PHP: How to determine the center of a Polygon

@Matthieu Sorry I forgot to add the function, I edit the code with the ComputeArea() function. — Adrian Cid Almaguer, Aug 03 '17 at 14:13

score 1 · Answer 6 · answered Jul 27 '17 at 18:22

This was my implementation in Java of the accepted solution, I added an extra conditional check because some of my polygons were flat and had no area, and rather than giving me the midpoint, it was returning (0,0). Thus in this case, I reference a different method which simply averages the vertices. The rounding at the end is because I wanted to keep my output object as integers even though it is imprecise, but I welcome you to remove that bit. Also, since all of my points were positive integers, the check made sense for me, but for you, adding an area check == 0 would also make sense.

private Vertex getCentroid() {

        double xsum = 0, ysum = 0, A = 0;
        for (int i = 0; i < corners.size() ; i++) {

            int iPlusOne = (i==corners.size()-1)?0:i+1;

            xsum += (corners.get(i).getX() + corners.get(iPlusOne).getX()) * (corners.get(i).getX() * corners.get(iPlusOne).getY() - corners.get(iPlusOne).getX() * corners.get(i).getY());
            ysum += (corners.get(i).getY() + corners.get(iPlusOne).getY()) * (corners.get(i).getX() * corners.get(iPlusOne).getY() - corners.get(iPlusOne).getX() * corners.get(i).getY());
            A += (corners.get(i).getX() * corners.get(iPlusOne).getY() - corners.get(iPlusOne).getX() * corners.get(i).getY());
        }
        A = A / 2;
        if(xsum==0 &&ysum==0)
        {
            area = averageHeight/2;
            return getMidpointCenter();
        }
        double x = xsum / (6 * A);
        double y = ysum / (6 * A);
        area = A;


        return new Vertex((int) Math.round(x), (int) Math.round(y));
    }

score 0 · Answer 7 · answered Jun 30 '19 at 17:44

Here is my implementation in Python, based off the C++ implementation from Joseph. I think it is clearer than the other python answer.

def find_centroid(polygon):
    """ Computes the centroid (a.k.a. center of gravity) for a non-self-intersecting polygon.

    Parameters
    ----------
    polygon : list of two-dimensional points (points are array-like with two elements)
        Non-self-intersecting polygon (orientation does not matter).

    Returns
    -------
    center_of_gravity : list with 2 elements
        Coordinates (or vector) to the centroid of the polygon.
    """
    offset = polygon[0]
    center_of_gravity = [0.0, 0.0]
    double_area = 0.0
    for ii in range(len(polygon)):
        p1 = polygon[ii]
        p2 = polygon[ii-1]
        f = (p1[0]-offset[0])*(p2[1]-offset[1]) - (p2[0]-offset[0])*(p1[1]-offset[1])
        double_area += f
        center_of_gravity[0] += (p1[0] + p2[0] - 2*offset[0]) * f
        center_of_gravity[1] += (p1[1] + p2[1] - 2*offset[1]) * f
    center_of_gravity[0] = center_of_gravity[0] / (3*double_area) + offset[0]
    center_of_gravity[1] = center_of_gravity[1] / (3*double_area) + offset[1]
    return center_of_gravity
    # If you want to return both the CoG and the area, comment the return above
    return center_of_gravity, abs(double_area/2)

score 0 · Answer 8 · answered Apr 10 '21 at 15:31

according to this answer

in C# :

public static Point findCentroid(List<Point> pts)
    {
        Point off = pts[0];
        double twicearea = 0;
        double x = 0;
        double y = 0;
        Point p1, p2;
        double f;
        for (int i = 0, j = pts.Count - 1; i < pts.Count; j = i++)
        {
            p1 = pts[i];
            p2 = pts[j];
            f = (p1.x - off.x) * (p2.y - off.y) - (p2.x - off.x) * (p1.y - off.y);
            twicearea += f;
            x += (p1.x + p2.x - 2 * off.x) * f;
            y += (p1.y + p2.y - 2 * off.y) * f;
        }

        f = twicearea * 3;

        return new Point(x / f + off.x, y / f + off.y);
    }

Center of gravity of a polygon

8 Answers8

Linked