4

As an extension and partial answer to my thread I wrote a simple algorithm that given a set of points(with xy coordinates) can form a non self-intersecting polygon.

Claim: Given an arbitrary set of points with different coordinates it is always possible to construct a regular or irregular, non self-intersecting polygon.

The algorithm:

Assume there is a set V containing all the vertices

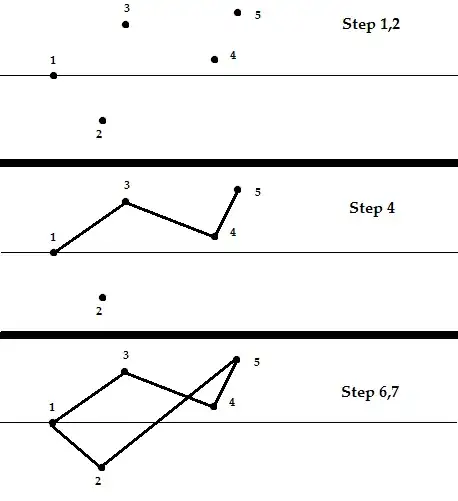
1) Sort all vertices in V by x-coordinate

2) Imagine a straight line (we'll call that "the divider") parallel to the x-axis which starting from the first node expands to infinity and divides/splits the vertices into two sets.

3) Now consider the two sets:

A = The set of all vertices above or on the divider line

B = The set of all remaining vertices

4) Starting at the leftmost vertex of A connect all vertices in A until you get to the rightmost

5) If the rightmost vertex of the sorted set V (the vertex with the biggest x coordinate) is not in A connect that last vertex (rightmost of A) with it.

6) Work backwards and starting from the rightmost vertex of the sorted set V (the vertex with the biggest x coordinate) connect all the vertices that are in B

7)Connect the first (leftmost vertex of B) vertex of B with the leftmost vertex of A

I think that the algorithm is correct and can't find a test that it would fail but maybe I'm missing something.

I would appreciate it if you could have a look and give me an example that wouldn't work if there is any(which I'm sure there must be).

Community
  • 1
  • 1
mixkat
  • 3,883
  • 10
  • 40
  • 58

5 Answers5

3

Here is a counterexample. When step 5 does not draw a line, it is possible to self intersect.

counterexample

Null Set
  • 5,374
  • 24
  • 37
  • Yup! just draw a similar one my self! Nicely laid out though! Thanks! Good thing is that I wont be needing the algorithm after all! – mixkat Mar 12 '11 at 01:27
2

I'm not sure I understand correctly what you're trying to do. In the other thread, and in the corresponding thread at math.SE (which brought me here), you said you had a polygon and were trying to find its center of gravity. Here you say you have a set of points and you want to construct a non-intersecting polygon from it. Those are two quite different things. As I mentioned at math.SE, if the polygons are not known to be convex, a set of points doesn't uniquely define a polygon -- so the algorithm you propose here may construct some arbitrary non-self-intersecting polygon (I haven't checked whether it successfully does that) but that may or may not bear any relation to the polygon you were originally interested in. Or did I misunderstand your question at math.SE and you actually only have some points and want to construct just any non-self-intersecting polygon from them and don't care that there may be several inequivalent solutions for this?

Community
  • 1
  • 1
joriki
  • 617
  • 5
  • 14
  • @joriki I'm sorry I didn't explain it properly! I was originally trying to find an algorithm that would calculate the center of gravity for any given polygon(self-intersecting or not). However since I dont have an actual polygon and only a set of points I thought that I can "draw" the polygon so that it never is self-intersecting. Thats what I'm trying to do with this algorithm basically.So that I can then apply the formula of the centroid. – mixkat Mar 11 '11 at 22:51
  • @mixkat: That sounds like a rather ill-defined problem. How do you get these points? And how do you know that the centroid of just any polygon you form from them is relevant? The centroids of different polygons you could construct from the same points could vary quite considerably. For instance, imagine a point lying almost between two other points, but slightly "inward" -- you can either connect it between those two points, or you can connect it between two points on the opposite side instead, with drastically different results. Perhaps what you're actually interested in is the convex hull?! – joriki Mar 11 '11 at 23:07
  • @joriki You're right the centroids could vary significantly.I need my final algorithm to be taking into account the coordinates of every point and thats why I'm not looking at the convex hull..As I said the main idea is to calculate the closest meeting point for a bunch of people.I suppose that the centroid of the polygon will not always be the most accurate result but it should be good enough i think. – mixkat Mar 11 '11 at 23:33
  • 1
    @mixkat: Sorry, I must have missed the "closest meeting point for a bunch of people" part; I don't know where you wrote that. In that case, I don't understand why you're bothering with polygons at all. Why aren't you simply calculating the center of gravity of these people? I.e. $\sum_{i=1}^n \vec{x}_i/n$. That's the solution to minimizing the sum of squares of the distances of the people from the meeting point. I see no reason to bring polygons into it. – joriki Mar 11 '11 at 23:39
  • @joriki Its ok!I wrote that as a comment in math.SE! How can I do that? Can you maybe provide a link or explain how this is possible?Again thanks a lot for your help!!! – mixkat Mar 11 '11 at 23:43
  • @mixkat: I don't understand the question -- the formula is in my previous comment -- that's how you do it, there's nothing more to it. What I wrote after the formula was just to explain why this is a good solution for your problem. Wikipedia has an article about the center of mass: http://en.wikipedia.org/wiki/Center_of_mass, but it doesn't have anything about the center of mass minimizing the sum of squares of distances. You can derive that by writing down the sum of squares of distances from an arbitrary point and differentiating it with respect to the coordinates of the point. – joriki Mar 12 '11 at 00:04
  • @mixkat: I should add that the Wikipedia article is about actual physical bodies that each have a mass $m_i$ -- in your case, unless you want to give different weights to the different people being close to the meeting point, you can set $m_i=1$ for everyone, which makes the sum in the denominator equal $n$, as in my formula above. – joriki Mar 12 '11 at 00:07
  • @joriki I like the way you put it "Why aren't you SIMPLY calculating the center of gravity" :) Sorry just one last question! In the above formula is $ an integral or..? Feel stupid already but maths is not one of my strengths sorry!!! – mixkat Mar 12 '11 at 00:24
  • @mixkat: I'm very sorry; it was certainly not my intention to make you feel stupid. I meant "simply" in the sense of much simpler than going to all the trouble of constructing polygons; I didn't mean to imply that it should be easy for you if you hadn't seen it before. Also sorry about the garbled formulas -- that's TeX input, which at math.SE is automatically converted to nice formulas, but apparently not here, so I'll write it out in plain text: you "simply" sum over the position vectors of all the people and divide the result by the number of people. E.g.: people at (1,2), (2,4), (3,3) ... – joriki Mar 12 '11 at 00:31
  • @mixkat: Then the sum of the position vectors is (6,9), and dividing by the number of people, 3, yields (2,3), which is the center of gravity -- if you draw it, you'll see that this is somewhere in the middle between all the people. – joriki Mar 12 '11 at 00:32
  • @joriki No no worries! It wasn't your fault it was me and my math skills! Is it really that simple? Cant believe I spent 2 days trying to figure this out! Sometimes you just overcomplicate things I suppose! I was only thinking of it as a polygon but its bloody coordinates isn't it? of course you can get the mean of them! Maaan!Thank you very very much! You have been very helpful indeed! – mixkat Mar 12 '11 at 00:41
2

I think I have a simpler algorithm that creates such a polygon. May be harder to implement in software but is much easier to describe in words.

  • Pick any point in the set as your start. Create a line at 0 angle starting from it.
  • start rotating the line around the point. The moment it meets any other point, draw an edge from the starting point to the newly found point.
  • continue rotating around the starting point, connecting any newly-found point with the last found.
  • at finish of the rotation, close the shape by meeting the start point.

In case of multiple finds on one direction, connect them picking one direction (say, starting with inner-most ending with outer-most)

The shape will be usually somewhat star-like, but fulfilling the requirements.

Computational execution would be like:

  • translate all points to coordinate set with origin[0,0] in one of the points.
  • convert all points to polar coordinate set
  • sort by: angle ascending, radius ascending.
  • connect all points in the sort order.
  • connect last to the first ([0,0]) point.
SF.
  • 13,549
  • 14
  • 71
  • 107
  • Appreciate the input however this would be a lot harder to implement in code. Looks like it could work (havent actually checked it) – mixkat Mar 11 '11 at 22:55
  • @joriki: I think you misunderstood the algorithm. It does NOT switch the rotation point as you go, and it will definitely work on all points. example: http://i54.tinypic.com/24zzt4m.png – SF. Mar 14 '11 at 09:13
  • You're right, I misunderstood the algorithm. Sorry about that. – joriki Mar 14 '11 at 09:47
1

I would prove it slightly differently by setting the "divider line" as a connection between left-most and right-most points, rather than parallel to x axis. It could happen that there are no points below or above the parallel-to-x line and that could cause trouble to your proof.

Also, connection (5) could lead to some self-intersections with the connections generated in point (6)

There is also a special case when all points are colinear and your polygon is degraded to a line.

We assume that the set V of vertices is finite ;)

Other than that - I believe your claim is true.

CygnusX1
  • 20,968
  • 5
  • 65
  • 109
  • Thanks for the reply!!! [1]"There is also a special case when all points are colinear and your polygon is degraded to a line." That is a valid point actually!!! [2]Could you give an example of that: "Also, connection (5) could lead to some self-intersections with the connections generated in point(6)". [3]"It could happen that there are no points below or above the parallel-to-x line and that could cause trouble to your proof." That's the same as [1] right??? – mixkat Mar 11 '11 at 22:43
0

I had the same problem in javascript and OpenLayers library. So this is my solution for detecting validity of a polygon in 'vectors' layer as a OpenLayers.Layer.Vector:

var ps = vectors.features[0].geometry.getVertices(), i, j, inx, x1, x2, x3, x4, y1, y2, y3, y4, x43, x21, y21, y43, y31, maxx12, maxx34, minx12, minx34;
ps.push(ps[0]);
for(i = 0; i < ps.length -1 ; i++ ) {
  x1 = ps[i].x; x2 = ps[i+1].x;
  y1 = ps[i].y; y2 = ps[i+1].y;
  for(j = i + 2; j < ps.length -1 ; j++ ) {
    x3 = ps[j].x; x4 = ps[j+1].x;
    y3 = ps[j].y; y4 = ps[j+1].y;
    x43 = x4 - x3; x21 = x2 - x1; y21 = y2 - y1; y43 = y4 - y3; y31 = y3 - y1;
    inx = ( x43*y21*x1 - x21*y43*x3 + y31*x21*x43 )/( x43*y21 - x21*y43 );
    if( x1 < x2 ){
      minx12 = x1; maxx12 = x2;
    } else {
      minx12 = x2; maxx12 = x1;
    }
    if( x3 < x4 ){
      minx34 = x3; maxx34 = x4;
    } else {
      minx34 = x4; maxx34 = x3;
    }
    if (minx12 < inx && inx < maxx12 && minx34 < inx && inx < maxx34 ){
      console.log('intersected!'+' ,x1: '+x1+' ,x2: '+x2+' ,inx: '+inx+' ,i: '+i+' ,j: '+j);

      return;
    }
  }
}

hope you enjoy it!!

hadilq
  • 1,023
  • 11
  • 25