How to visually connect 2 circles?

Question

We know 2 circle's x and y center position, and the radius is the same. I want to visually connect the circles without looping the draw ellipse for each point on the line what connects the 2 circle's center.

From this:

To this:

Code:

int radius = 75;

int x1 = 100;
int y1 = 200;

int x2 = 300;
int y2 = 100;

g.FillEllipse(Brushes.Blue, new Rectangle(x1 - radius / 2, y1 - radius / 2, radius, radius));
g.FillEllipse(Brushes.Blue, new Rectangle(x2 - radius / 2, y2 - radius / 2, radius, radius));

Answer 1

A solution for when the Circles don't have the same Diameter.

The first information needed is the distance between the Centers of two Circles.
To calculate it, we use the Euclidean distance applied to a Cartesian plane:

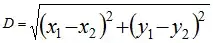
Where (x1, y1) and (x2, y2) are the coordinates of the Centers of two Circles.
We also need to know the Direction (expressed as a positive or negative value): the calculated [Distance] will always be positive.

in C# it, it can be coded as:

float Direction = (Circle1Center.X > Circle2Center.X) ? -1 : 1;
float Distance = (float)Math.Sqrt(Math.Pow(Circle1Center.X - Circle2Center.X, 2) + 
                                  Math.Pow(Circle1Center.Y - Circle2Center.Y, 2));
Distance *= Direction;

Now, we have the Distance between the Centers of two Circles, which also expresses a direction.
We also need to know how this virtual line - connecting the two Centers - is rotated in relation to our drawing plane. In the figure below, the Distance can be viewed as the hypotenuse of a right triangle h = (A, B). The C angle is determined by the intersection of the straight lines, parallel to the axis, that cross the Centers of the Circles.

We need to calculate the angle Theta (θ).
Using the Pythagorean theorem, we can derive that the Sine of the angle Theta is Sinθ = b/h (as in the figure)

Using the Circles' Centers coordinates, this can be coded in C# as:
(Distance is the triangle's hypotenuse)

float SinTheta = (Math.Max(Circle1Center.Y, Circle2Center.Y) - 
                  Math.Min(Circle1Center.Y, Circle2Center.Y)) / Distance;

SinTheta expresses an angle in Radians. We need the angle expressed in Degrees: the Graphics object uses this measure for its world transformation functions.

float RotationAngle = (float)(Math.Asin(SinTheta) * (180 / Math.PI));

Now, we need to build a Connector, a shape that links the 2 Circles. We need a Polygon; a Rectangle can't have different pairs of sides (we are considering Circles with different Diameters).
This Polygon will have the longer sides = to the Distance between the Circles Centers, the shorter sides = to the Circles Diameters.

To build a Polygon, we can use both Graphics.DrawPolygon and GraphicsPath.AddPolygon. I'm choosing the GraphicsPath method, because a GraphicsPath can hold more that one shape and these shapes can interact, in a way.

To connect the 2 considered Circles with a Polygon, we need to rotate the Polygon using the RotationAngle previously calculated.
A simple way to perform the rotation, is to move the world coordinates to the Center of one of the Circles, using the Graphics.TranslateTransform method, then rotate the new coordinates, using Graphics.RotateTransform.

We need to draw our Polygon positioning one of the short sides - corresponding to the Diameter of the Circle which is the center of the coordinates transformation - in the center of the Cirle. Hence, when the rotation will be applied, it's short side it will be in the middle of this transformation, anchored to the Center.

Here, figure 3 shows the positioning of the Polygon (yellow shape) (ok, it looks like a rectangle, never mind);
in figure 4 the same Polygon after the rotation.

Notes:
As TaW pointed out, this drawing needs to be performed using a SolidBrush with a non-transparent Color, which is kind of disappointing.
Well, a semi-transparent Brush is not forbidden, but the overlapping shapes will have a different color, the sum of the transparent colors of the intersections.

It is however possible to draw the shapes using a semi-transparent Brush without a Color change, using the GraphicsPath ability to fill its shapes using a color that is applied to all the overlapping parts. We just need to change the default FillMode (see the example in the Docs), setting it to FillMode.Winding.

Sample code:
In this example, two couples of Circles are drawn on a Graphics context. They are then connected with a Polygon shape, created using GraphicsPath.AddPolygon().
(Of course, we need to use the Paint event of a drawable Control, a Form here)

The overloaded helper function accepts both the Circles' centers position, expressed as a PointF and a RectangleF structure, representing the Circles bounds.

This is the visual result, with full Colors and using a semi-transparent brush:

using System.Drawing;
using System.Drawing.Drawing2D;

private float Radius1 = 30f;
private float Radius2 = 50f;

private PointF Circle1Center = new PointF(220, 47);
private PointF Circle2Center = new PointF(72, 254);
private PointF Circle3Center = new PointF(52, 58);
private PointF Circle4Center = new PointF(217, 232);


private void form1_Paint(object sender, PaintEventArgs e)
{
    e.Graphics.CompositingQuality =  CompositingQuality.GammaCorrected;
    e.Graphics.PixelOffsetMode = PixelOffsetMode.Half;
    e.Graphics.SmoothingMode = SmoothingMode.AntiAlias;

    DrawLinkedCircles(Circle1Center, Circle2Center, Radius1, Radius2, Color.FromArgb(200, Color.YellowGreen), e.Graphics);
    DrawLinkedCircles(Circle3Center, Circle4Center, Radius1, Radius2, Color.FromArgb(200, Color.SteelBlue), e.Graphics);

    //OR, passing a RectangleF structure
    //RectangleF Circle1 = new RectangleF(Circle1Center.X - Radius1, Circle1Center.Y - Radius1, Radius1 * 2, Radius1 * 2);
    //RectangleF Circle2 = new RectangleF(Circle2Center.X - Radius2, Circle2Center.Y - Radius2, Radius2 * 2, Radius2 * 2);

    //DrawLinkedCircles(Circle1, Circle2, Color.FromArgb(200, Color.YellowGreen), e.Graphics);
}

Helper function:

public void DrawLinkedCircles(RectangleF Circle1, RectangleF Circle2, Color FillColor, Graphics g)
{
    PointF Circle1Center = new PointF(Circle1.X + (Circle1.Width / 2), Circle1.Y + (Circle1.Height / 2));
    PointF Circle2Center = new PointF(Circle2.X + (Circle2.Width / 2), Circle2.Y + (Circle2.Height / 2));
    DrawLinkedCircles(Circle1Center, Circle2Center, Circle1.Width / 2, Circle2.Width / 2, FillColor, g);
}

public void DrawLinkedCircles(PointF Circle1Center, PointF Circle2Center, float Circle1Radius, float Circle2Radius, Color FillColor, Graphics g)
{
    float Direction = (Circle1Center.X > Circle2Center.X) ? -1 : 1;
    float Distance = (float)Math.Sqrt(Math.Pow(Circle1Center.X - Circle2Center.X, 2) +
                                      Math.Pow(Circle1Center.Y - Circle2Center.Y, 2));
    Distance *= Direction;

    float SinTheta = (Math.Max(Circle1Center.Y, Circle2Center.Y) -
                      Math.Min(Circle1Center.Y, Circle2Center.Y)) / Distance;

    float RotationDirection = (Circle1Center.Y > Circle2Center.Y) ? -1 : 1;
    float RotationAngle = (float)(Math.Asin(SinTheta) * (180 / Math.PI)) * RotationDirection;

    using (GraphicsPath path = new GraphicsPath(FillMode.Winding))
    {
        path.AddEllipse(new RectangleF(-Circle1Radius, -Circle1Radius, 2 * Circle1Radius, 2 * Circle1Radius));
        path.AddEllipse(new RectangleF(-Circle2Radius + (Math.Abs(Distance) * Direction),
                                       -Circle2Radius, 2 * Circle2Radius, 2 * Circle2Radius));
        path.AddPolygon(new[] {
            new PointF(0, -Circle1Radius),
            new PointF(0, Circle1Radius),
            new PointF(Distance, Circle2Radius),
            new PointF(Distance, -Circle2Radius),
        });
        path.AddEllipse(new RectangleF(-Circle1Radius, -Circle1Radius, 2 * Circle1Radius, 2 * Circle1Radius));
        path.AddEllipse(new RectangleF(-Circle2Radius + (Math.Abs(Distance) * Direction),
                                       -Circle2Radius, 2 * Circle2Radius, 2 * Circle2Radius));

        path.CloseAllFigures();

        g.TranslateTransform(Circle1Center.X, Circle1Center.Y);
        g.RotateTransform(RotationAngle);

        using (SolidBrush FillBrush = new SolidBrush(FillColor)) {
            g.FillPath(FillBrush, path);
        }
        g.ResetTransform();
    }
}

Answer 2

As the other answers so far slightly miss the correct solution, here is one that connects two circles of equal size:

using (Pen pen = new Pen(Color.Blue, radius)
 { EndCap = LineCap.Round, StartCap = LineCap.Round }  )
     g.DrawLine(pen, x1, y1, x2, y2);

Notes:

• Usually is is good idea to set the smoothing mode of the graphics object to anti-alias..

• To connect two circles of different sizes will take some math to calculate the four outer tangent points. From these one can get a polygon to fill or, if necessary one could create a GraphicsPath to fill, in case the color has an alpha < 1.

• Jimi's comments point to a different solution that make use of GDI+ transformation capabilities.

• Some of the answers or comments refer to the desired shape as an oval. While this ok in common speech, here, especially when geometry books are mentioned, this is wrong, as an oval will not have any straight lines.

• As Jimi noted, what you call radius is really the diameter of the circles. I left the wrong term in the code but you should not!

Answer 3

Pseudo style:

  circle1x;
    circle1y;

circle2x;
circle2y;


midx=circle1x-circle2x;
midy=circle2x-circle2x;

draw circle at midx midy;

repeat for midx midy, in both directions. add another circle. honestly man, this isnt worth it,in order to make it smooth, you will need several circles. you need to draw an oval using the center of both circles as the two centers of your oval