Find Distance to Decision Boundary in Decision Trees

Question

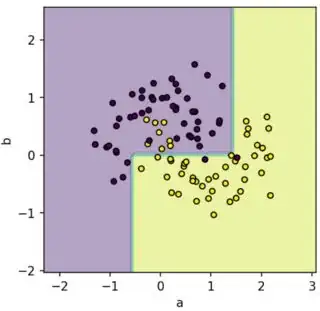
I want to find the distance of samples to the decision boundary of a trained decision trees classifier in scikit-learn. The features are all numeric and the feature space could be of any size.

I have this visualization so far for an example 2D case based on here:

import numpy as np
import matplotlib.pyplot as plt

from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_moons

# Generate some example data
X, y = make_moons(noise=0.3, random_state=0)

# Train the classifier
clf = DecisionTreeClassifier(max_depth=2)

clf.fit(X, y)

# Plot
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))

Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor='k')
plt.xlabel('a'); plt.ylabel('b');

I understand that for some other classifiers like SVM, this distance can be mathematically calculated [1, 2, 3]. The rules learned after training a decision trees define the boundaries and may also be helpful to algorithmically calculate the distances [4, 5, 6]:

# Plot the trained tree
from sklearn import tree
import graphviz 
dot_data = tree.export_graphviz(clf, feature_names=['a', 'b'],  class_names=['1', '2'], filled=True)  
graph = graphviz.Source(dot_data)  

Answer 1

Since there can be multiple decision boundaries around a sample, I'm going to assume distance here refers to distance to nearest decision boundary.

The solution is a recursive tree traversal algorithm. Note that decision tree doesn't allow a sample to be on boundary, like e.g. SVM, each sample in feature space must belong to one of the classes. So here we will keep modifying the sample's feature in small steps, and whenever that leads to a region with a different label (than one originally assigned to the sample by trained classifier), we assume we've reached decision boundary.

In detail, like any recursive algorithm, we have two main cases to consider:

1. Base case i.e. we're at a leaf node. We simply check if the current sample have different label: if so then return it, otherwise return None.
2. Non leaf nodes. There are two branches, we send the sample to both. We don't modify the sample to send it to branch it would naturally take. But before sending it to the other branch, we look at the (feature, threshold) pair of the node, and modify the sample's given feature just enough to push it on the opposite side of threshold.

Complete python code:

def f(node,x,orig_label):
    global dt,tree
    if tree.children_left[node]==tree.children_right[node]: #Meaning node is a leaf
        return [x] if dt.predict([x])[0]!=orig_label else [None]

    if x[tree.feature[node]]<=tree.threshold[node]:
        orig = f(tree.children_left[node],x,orig_label)
        xc = x.copy()
        xc[tree.feature[node]] = tree.threshold[node] + .01
        modif = f(tree.children_right[node],xc,orig_label)
    else:
        orig = f(tree.children_right[node],x,orig_label)
        xc = x.copy()
        xc[tree.feature[node]] = tree.threshold[node] 
        modif = f(tree.children_left[node],xc,orig_label)
    return [s for s in orig+modif if s is not None]

This is going to return us a list of samples that lead to leaves with different label. All we need to do now is to take the nearest one:

dt =  DecisionTreeClassifier(max_depth=2).fit(X,y)
tree = dt.tree_
res = f(0,x,dt.predict([x])[0]) # 0 is index of root node
ans = np.min([np.linalg.norm(x-n) for n in res]) 

For illustration:

Blue is the original sample, yellow is the nearest sample "on" decision boundary.

Answer 2

Decision tree does not learn to draw a decision boundary. It tries to split the tree based on the maximum information gain point. For this process, decision tree algorithm uses entropy or gini indexes.

Because of this reason, you cannot find the distance between the points and the decision boundary( there is no decision boundary).

If you want you can calculate the distance between the points and the lines that you draw on graphic. So it approximately gives some results.