1

I want to find index of the nearest transition in a numpy ndarray of integers given a current index in an efficient manner. Transition means a change of value.

For example, in the 2D array below, the right output for location (2,4) would be (3,6) (transition from Class 1 to Class 8) at the approximate distance of 2.236. In case of more than one optimum, returning any would suffice. 

import seaborn as sns
import numpy as np

step_size = [1,1]  # size of step in each dimension
arr = np.array([[6,6,1,1,1,1,1,1,1,8],[6,1,1,1,1,1,1,1,8,8],[6,1,1,1,1,1,1,1,8,8],[6,1,1,1,1,1,8,8,8,8],[6,6,1,1,1,1,1,8,8,8]])
sns.heatmap(arr, annot=True, cbar=False)

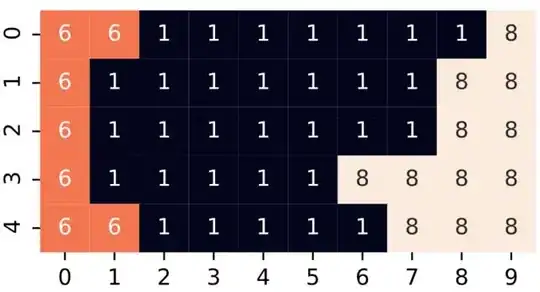
enter image description here

The application is to estimate distances to boundaries. Such as a sample's distance to decision boundary in classification algorithms where an accurate algorithm or formula for that is not available (like xgboost, and unlike SVM and decision trees).

Reveille
  • 4,359
  • 3
  • 23
  • 46

1 Answers1

0

To detect a change, perform some type of derivative on the matrix. This can be done with a Laplacian kernel. In this kernel, you may define what type of change you are looking for, but for this, I simply told it to look for change in the left, right, up, and down squares (not the corners). Then find the closest square which has some change in it. This will not produce the same result as you wish, but rather will find the closest square which is associated with the boundary ((3, 5) in your example). You may modify it, as well as handle multiple optimums, to your liking. As far as efficiency goes, I'm not saying this is going to win any prizes, but notice that any looping is happening implicitly within numpy/scipy operations (which are optimized).

import numpy as np
import scipy

# This function referenced from: 
#   https://stackoverflow.com/questions/61628380/calculate-distance-from-all- 
#   points-in-numpy-array-to-a-single-point-on-the-basis
def distmat_v2(a, index):
    i,j = np.indices(a.shape, sparse=True)
    return np.sqrt((i-index[0])**2 + (j-index[1])**2)

# Your original array.
arr = np.array([[6,6,1,1,1,1,1,1,1,8],[6,1,1,1,1,1,1,1,8,8], 
      [6,1,1,1,1,1,1,1,8,8],[6,1,1,1,1,1,8,8,8,8],[6,6,1,1,1,1,1,8,8,8]])

# Extract size of array for converting np.argmin output to array location.
r, c = np.shape(arr)

# Define and apply the edge detection kernel to the array. Then test logical 
#   equality with zero. This will set a 'True' for every element that had some 
#   type of change detected and 'False' otherwise.
edge_change_detection_kernel = np.array([[0,-1,0],[-1,4,-1],[0,-1,0]])
# edge_and_corner_change_detection_kernel = np.array([[-1,-1,-1],[-1,8,-1], 
#      [-1,-1,-1]])
change_arr = scipy.signal.convolve2d(arr, edge_change_detection_kernel, 
      boundary='symm', mode='same') != 0

# Calculate the distance from a certain point, say (2, 4), to all other points 
#   in the matrix.
distances_from_point = distmat_v2(arr, (2, 4))

# Element-wise multiply the logical matrix with the distances matrix. This keeps 
#   all the distances which had a change in the same square. It discards the 
#   distances which didn't have a change in the square.
changed_locations_distances_from_point = np.multiply(change_arr, 
      distances_from_point)

# Test for the smallest distance that is left after keeping only the changing 
#   squares. However, some locations will have zero in them, so set those values 
#   to infinity before testing the smallest value. This will find the smallest, 
#   non-zero distance.
closest_change_square_to_point = np.where(
  changed_locations_distances_from_point > 0, 
  changed_locations_distances_from_point, np.inf).argmin()

# Find the array location where the argmin function found the appropriate value.
print(f'row {int(closest_change_square_to_point/c)}')
print(f'col {closest_change_square_to_point%c}')
greenerpastures
  • 168
  • 8