0

I have coordinates corresponding to a set of 2D contours, each corresponding to different heights. These contours do not draw out a perfect ellipsoid in 3D, and instead what I would like to do is to find the best fitting ellipsoid. I do not have any knowledge on the origin of this ellipsoid.

My first thought was to incorporate some type of least squares algorithm, where I find the ellipsoid parameters that minimize the distance between points. I imagine this would be quite expensive and not too far from a brute force approach. I am convinced there is a more elegant and efficient way of doing this. If there is an existing library that handles this (preferably in Python) that would be even better.

I have already seen a related question (Fitting an ellipsoid to 3D data points), but figured I would ask again as it has been over a decade since that post.

APM500
  • 85
  • 1
  • 7
  • So you have a series of slices that you want to assemble into a 3D shape. You can fit an ellipse into each slice, but constraint the center between all the slices. I am not sure how to do this. – John Alexiou Feb 28 '22 at 19:06
  • 1
    @JohnAlexiou Yeah but the slices do not outline the full ellipse, for example they may outline just a small fraction of the ellipse. I suspect this fraction is enough to define an ellipse. Also the slices themselves are not perfect cross sections which is why I would have to settle for some kind of optimal fit. – APM500 Feb 28 '22 at 19:11
  • 1
    I doubt that the specific problem of fitting an ellipsoid to contours has been studied, and you have to resort to fitting to independent points. Most published methods seem to rely on the minimization of total distance, which leads to the Levenberg-Marquardt algorithm (as the problem is nonlinear, you can't escape that). I would not recommend fitting individual ellipses, then fitting an ellipsoid to the ellipses. –  Mar 01 '22 at 09:10
  • Of interest: https://projet.liris.cnrs.fr/imagine/pub/proceedings/ICPR-2012/media/files/0437.pdf –  Mar 01 '22 at 09:16
  • see [Algorithms: Ellipse matching](https://stackoverflow.com/a/36054594/2521214) especially the geometric approach its applicable on 3D easily too, the angular difference is the "same" as dot between tangents so no need for goniometrics. Also you can use [3D OBB](https://stackoverflow.com/a/62284464/2521214) or PCA/Eigenvectors – Spektre Mar 01 '22 at 09:42

1 Answers1

3

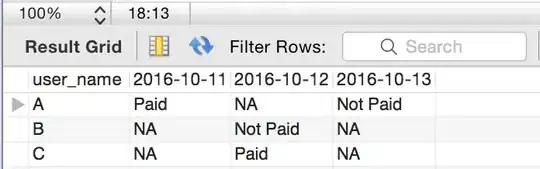
So you have a set of (x,y) values for each contour, which describe a portion of an ellipse (blue dots below).

scr1

The best fit ellipse is described by the general equation

A x^2 + B y^2 + 2C x y + 2D x + 2E y = 1

and once the coefficients (A,B,C,D,E) are found, the ellipse of fully described. See below in how to find the the curve coordinates (x,y) from the coefficients and a parameter t=0 .. 1.

To find the coefficients of the ellipse, form 5 vectors, each a column of a n×5 matrix Q

for i = 1 to n
  Q(i,1) = x(i)^2
  Q(i,2) = y(i)^2
  Q(i,3) = 2*x(i)*y(i)
  Q(i,4) = 2*x(i)
  Q(i,5) = 2*y(i)
next i

and a vector K filled with 1 for the right-hand side

for i = 1 to n
  K(i) = 1.0
next i

scr2

Find the coefficients using a least-squares fit with some linear algebra

[A,B,C,D,E] = inv(tr(Q)*Q)*tr(Q)*K

where tr(Q) is the transpose of Q and * is matrix/vector product

scr3

Now we need to extract the geometric properties of the ellipse from the coefficient. I want to have a the semi-major axis, b the semi-minor axis, φ the rotation angle, xc the x-axis center, yc the y-axis center.

xc = -(B*D-C*E)/(A*B-(C^2))
yc = -(A*E-C*D)/(A*B-(C^2))
φ = atan( 2*C/(A-B) )/2
a = SQRT(2*(A*(B+E^2)+B*D^2-C*(C+2*D*E))/((A*B-C^2)*(A+B-SQRT((A-B)^2+4*C^2))))
b = SQRT(2*(A*(B+E^2)+B*D^2-C*(C+2*D*E))/((A*B-C^2)*(A+B+SQRT((A-B)^2+4*C^2))))

Finally to plot the ellipse you need to generate a set of points (x,y) from the curve parameter t=0..1 using the above 5 coefficients.

  1. Generate the centered aligned coordinates (u,v) with

    u = a*cos(2*π*t)
v = b*sin(2*π*t)

  2. Generate the centered rotated coordinates (x',y') with

    x' = u*cos(φ) - v*sin(φ)
y' = u*sin(φ) + v*cos(φ)

  3. Generate the ellipse coordinates (x,y) with

    x = x' + xc
y = y' + yc

The result is observed above in the first picture.

scr4

Now for the total solution, each 2D slice would have its own ellipse. But all the slices would not generate an ellipsoid this way.

Extending the above into 3D coordinates (x,y,z) is doable, but the math is quite involved and I feel [SO] is not a good place to develop such an algorithm. You can hack it together, by finding the average center for each slice (weighted by the ellipse area π*a*b). Additionally, the rotation angle should be the same for all contours, and so another averaging is needed. Finally, the major and minor axis values would fall on an elliptical curve along the z-axis and it would require another least-fit solution. This one is driven by the equation

(x/a)^2 + (y/b)^2 + (z/c)^2 = 1

but rather in the aligned coordinates (u,v,w)

(u/a)^2 + (v/b)^2 + (w/c)^2 = 1

John Alexiou
  • 28,472
  • 11
  • 77
  • 133
  • 2
    Thank you for the detailed response! I had something similar to what you suggested in mind, it's the extension to 3D that has been causing me some issues. My current approach is to frame it as an optimization problem and let some solver minimize the distance from my points to an ellipse for some given parameters. Though I feel this would be incredibly expensive. – APM500 Feb 28 '22 at 23:16
  • Thanks again for the detailed answer. I made a followup post regarding your approach (https://math.stackexchange.com/questions/4399677/finding-foci-coordinates-of-rotated-ellipse) and was wondering if you could take a look. – APM500 Mar 09 '22 at 20:18