Fitting an ellipsoid to 3D data points

Question

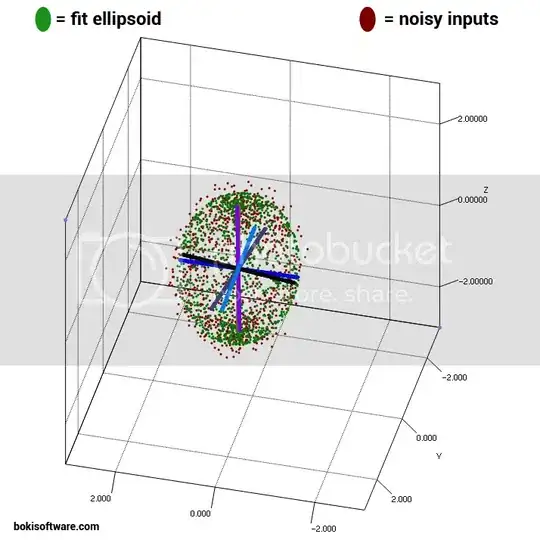
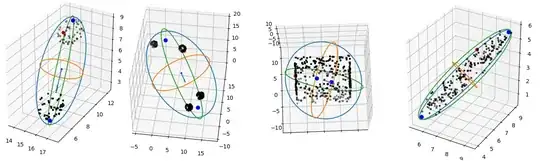
I have a large set of 3D data points to which I want to fit to an ellipsoid.

My maths is pretty poor, so I'm having trouble implementing the least squares method without any math libraries.

Does anyone know of or have a piece of code that can fit an ellipsoid to data which I can plug straight into my project? In C would be best, but it should be no problem for me to convert from C++, Java, C#, python etc.

EDIT: Just being able to find the centre would be a huge help too. Note that the points aren't evenly spaced so taking the mean won't result in the centre.

Do you expect your points to fall on the surface of the ellipsoid or do you expect your points to be in an ellipsoidal cloud? — ellisbben, Sep 01 '11 at 15:13
I expect them to fall on the surface of an ellipsoid, so the centre is hollow. — Hannesh, Sep 01 '11 at 16:12

score 10 · Answer 1 · answered Nov 21 '11 at 17:56

here you go:

This paper describes fitting an ellipsoid to multiple dimensions AS WELL AS finding the center for the ellipois. Hope this helps,

http://www.physics.smu.edu/~scalise/SMUpreprints/SMU-HEP-10-14.pdf

(btw, I'm assuming this answer is a bit late, but I figured I would add this solution for anyone who stumbles across your question in search for the same thing :)

score 2 · Answer 2 · edited May 23 '17 at 12:09

2

If you want the minimum-volume enclosing ellipsoid, check out this SO answer for a bounding ellipsoid.

If you want the best fitting ellipse in a least-squares sense, check out this MATLAB code for error ellipsoids where you find the covariance matrix of your mean-shifted 3D points and use that to construct the ellipsoid.

edited May 23 '17 at 12:09

Community

1
1

answered Sep 01 '11 at 16:40

Jacob

34,255
14
110
165

score 1 · Answer 3 · edited Feb 08 '17 at 14:38

I could not find a good Java based algorithm for fitting an ellipsoid, so I ended up writing it myself. There were some good algorithms for an ellipse with 2D points, but not for an ellipsoid with 3D points. I experimented with a few different MATLAB scripts and eventually settled on Yury Petrov's Ellipsoid Fit. It fits an ellipsoid to the polynomial Ax^2 + By^2 + Cz^2 + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Iz = 1. It doesn't use any constraints to force an ellipsoid, so you have to have a fairly large number of points to prevent a random quardic from being fit instead of the ellipsoid. Other than that, it works really well. I wrote a small Java library using Apache Commons Math that implements Yury Petrov's script in Java. The GIT repository can be found at https://github.com/BokiSoft/EllipsoidFit.

score 1 · Answer 4 · answered Feb 15 '17 at 16:30

We developed a set of Matlab and Java codes to fit ellipsoids here: https://github.com/pierre-weiss

You can also check our open-source Icy plugin. The following tutorial can be helpful: https://www.youtube.com/endscreen?video_referrer=watch&v=nXnPOG_YCxw

Note: most of the existing codes fit a generic quadric and do not impose an ellipsoidal shape. To get more robustness, you need to go to convex programming rather than just linear algebra. This is what is done in the indicated sources.

Cheers, Pierre

halt9k · Answer 5 · 2023-03-03T05:18:46.723

Here is unstrict solution with fast and simple random search approach*. Best side - no heavy linear algebra library required**. Seems it worked fine for mesh collision detection.

Is assumes that ellipsoid center matches cloud center and then uses some sort of mirrored average to search for main axis.

Full working code is slightly bigger and placed on git, idea of main axis search is here:

np.random.shuffle(pts)

pts_len = len(pts)
pt_average =  np.sum(pts, axis = 0) / pts_len

vec_major = pt_average * 0
minor_max, major_max = 0, 0

# may be improved with overlapped pass, 
for pt_cur in pts:
    vec_cur = pt_cur - pt_average
    proj_len, rej_len = proj_length(vec_cur, vec_major)

    if proj_len < 0:
        vec_cur = -vec_cur
    vec_major += (vec_cur - vec_major) / pts_len

    major_max = max(major_max, abs(proj_len))
    minor_max = max(minor_max, rej_len)

It can be improved/optimized even more at some points. Examples what it will produce:

And full experiment code with plots

*_{i.e. adjusting code lines randomly until they work}
**_{was actually reason to figure out this solution}

andand · Accepted Answer · 2011-09-01T17:56:03.113

1

Least Squares data fitting is probably a good methodology give the nature of the data you describe. The GNU Scientific Library contains linear and non-linear least squares data fitting routines. In your case, you may be able to transform your data into a linear space and use linear least-squares, but that would depend on your actual use case. Otherwise, you'll need to use non-linear methods.

edited Sep 01 '11 at 17:56

answered Sep 01 '11 at 16:21

andand

17,134
11
53
79

score 0 · Answer 7 · edited May 23 '17 at 11:45

0

I have just gone through the same process. Here is a python module which is based on work by Nima Moshtagh. Referenced in many places but also in this question about a Bounding ellipse

This module also handles plotting of the final ellipsoid. Enjoy!

https://github.com/minillinim/ellipsoid/blob/master/ellipsoid.py

edited May 23 '17 at 11:45

Community

1
1

answered Feb 20 '13 at 14:06

minillinim

690
6
10

score 0 · Answer 8 · answered Feb 21 '13 at 15:10

0

I ported Yury Petrov's least-squares Matlab fitter to Java some time ago, it only needs JAMA: https://github.com/mdoube/BoneJ/blob/master/src/org/doube/geometry/FitEllipsoid.java

answered Feb 21 '13 at 15:10

mdoube

3
2

You should like to the original Matlab source as well as include links/explanations for JAMA, since the question states the Java code must be portable to C. – Esoteric Screen Name Feb 21 '13 at 15:33
Sure:Matlab source http://www.mathworks.com/matlabcentral/fileexchange/24693-ellipsoid-fit – mdoube Feb 21 '13 at 17:13
JAMA is a Java matrix library - similar libraries must exist for C/C++ http://math.nist.gov/javanumerics/jama/ – mdoube Feb 21 '13 at 17:15

Krešimir Prcela · Answer 9 · 2011-09-01T15:40:51.037

0

I have an idea. Approximately solution, not the best but will keep points inside. In XY plane find the radius R1 that will obtain all points. Same do for the XZ plane (R2) and YZ plane (R3). Then use the maximums on each axes. A=max(R1,R2), B=max(R1,R3) and C=max(R2,R3). But, first of all find the average (center) of all points and align it to origin.

edited Sep 01 '11 at 15:40

answered Sep 01 '11 at 15:33

Krešimir Prcela

4,257
33
46

That's what I've been doing until now. The problem is that it doesn't find the actual maximum of the ellipsoid. Also, I wish the average of all points were the centre! But that only works if the points are evenly distributed on the surface. – Hannesh Sep 01 '11 at 16:19
Well, it is not such good idea. :) it is more complex than it looks at first moment. – Krešimir Prcela Sep 01 '11 at 19:59

Fitting an ellipsoid to 3D data points

9 Answers9

Linked