0

Find root of implicit function in Mathematica

I have an implicit function, for example:

f(x,y) = x^3 + x*y + y^2 - 36

I want to find the root, ie solutions to the equation f(x,y) = 0

Drawing the solution is easy:

ContourPlot[x^3 + x*y + y^2 - 36 == 0, {x, -2 Pi, 2 Pi}, {y, -3 Pi, 3 Pi}]

however I would like to have the data that is in the plot and not only the visual plot. So how do I find the data of the plot?

h02h001
  • 167
  • 4
  • 11
  • Erm, well, you have the data that you need in the function itself. If `f[x_,y_]=x^3 - x*y + y^2 - 36`, then for any `x` and `y` you want, you can find `f[x,y]`. But since you want to find the roots of this function, they lie on the curve given in this link: http://www.wolframalpha.com/input/?i=Solve%5Bx^3+%2B+x*y+%2B+y^2+-+36%3D%3D0%2C{x%2Cy}%5D (sorry, not all of the link is highlighted...you'll need to copy and paste it into your browser). –  Sep 09 '11 at 03:03
  • He wants the values of x and y where `f[x,y]==0`, not the value of any old `f[x,y]`. – Verbeia Sep 09 '11 at 03:05
  • that is a good question. i.e. how to get data OUT of a plot once it is made. i.e. p=ContourPlot[ x^3 + x*y + y^2 - 36 == 0, {x, -2 Pi, 2 Pi}, {y, -3 Pi, 3 Pi}]; Now how to get the data out of 'p' is what I think OP is asking. – Nasser Sep 09 '11 at 03:13
  • YES. Now how to get the data out of 'p' ? – h02h001 Sep 09 '11 at 03:35
  • You get it by looking at the curve(s) given when you solve for one of `x` or `y` in terms of the other. –  Sep 09 '11 at 05:37

3 Answers3

3

I would encourage you to explore the documentation on equation solving and particularly the Solve and NSolve functions.

EDIT

p = ContourPlot[x^3 + x*y + y^2 - 36 == 0, {x, -2 Pi, 2 Pi}, {y, -3 Pi, 3 Pi}]
p //InputForm

Copy and paste the bit you need.

Alternatively, and in my view a better solution to your actual problem.

sol = Solve[x^3 + x*y + y^2 - 36 == 0,{x}][[1]]

You might need some options to get the right solution.

Table[{x/. sol,y},{y, -3 Pi, 3 Pi, 0.02}]
Verbeia
  • 4,400
  • 2
  • 23
  • 44
  • i.e. how to get data OUT of a plot once it is made. i.e. p=ContourPlot[ x^3 + x*y + y^2 - 36 == 0, {x, -2 Pi, 2 Pi}, {y, -3 Pi, 3 Pi}]; Now how to get the data out of 'p' ? – h02h001 Sep 09 '11 at 03:33
  • 1
    Well, that wasn't your original question. I don't have Mathematica on the machine I'm using but see the edit to the answer. – Verbeia Sep 09 '11 at 04:23
  • @h02h001 in your parallel question asking the same thing about Matlab, you did explicitly say "how to get data OUT of a plot once it is made?" http://stackoverflow.com/questions/7356551/find-root-of-implicit-function-in-matlab You didn't for this question, but anyway, in Mathematica the better way is not to draw the figure and get the data out of it, but to just work out the solution directly. – Verbeia Sep 09 '11 at 06:13
  • //InputForm is OK ！ Thank you very much. Some equations can not use Solve、 NSolve to solution. Such as： Solve[E^(-(1/20) (-50 + y)^2) y - y Erf[125 - 9 y] + x y Erf[50 - 9 x y] == 0, {x}] NSolve[E^(-(1/20) (-50 + y)^2) y - y Erf[125 - 9 y] + x y Erf[50 - 9 x y] == 0, {x}] Do you know the algorithm for ContourPlot? – h02h001 Sep 09 '11 at 08:37
  • //InputForm is OK ！ Thank you very much. – h02h001 Sep 09 '11 at 08:45
3

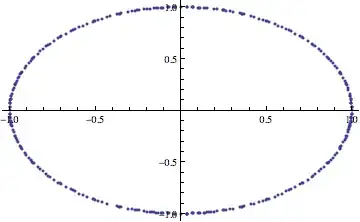
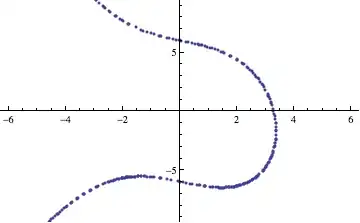
I'm not sure if I am interpreting your second question properly, but assuming you require a list of (x,y) points from the generated ContourPlot, one way of doing this might be the following:

plot = ContourPlot[
  x^3 + x*y + y^2 - 36 == 0, {x, -2 Pi, 2 Pi}, {y, -3 Pi, 3 Pi}]

To obtain a list of points

points = Cases[Normal@plot, x_Line :> First@x, Infinity];

'Take a look' with ListPlot

ListPlot[points, PlotRange -> {{-2 Pi, 2 Pi}, {-3 Pi, 3 Pi}}]

giving

enter image description here

Edit

Nasser has correctly pointed out that this question has been addressed before. Here is one link to essentially the same question and this answer by Szabolcs is relevant.

As regards the answer given above, this method is probably more direct:

points2 = Cases[plot, x_GraphicsComplex :> First@x, Infinity]

Finally, I should acknowledge " LunchTime Playground. Fun with Mathematica: How to extract points from a plot", see here, which gives both methods suggested above (and which I now use routinely).

Edit 2

This method is an improvement on method 1 above, as the points are obtained as a list of {x,y} values (list-of-lists) without any extraneous { }. 

Cases[Normal@plot, Line[{x__}] :> x, Infinity]

An article by Paul Abbott in the Mathematica Journal Vol 7, No 2, pp 108-112, 1998, Finding Roots in an Interval, gives a lot of useful information and is available here

He points out the the following also work

Cases[Normal@plot, _Line, -1][[1, 1]]

and(!)

plot[[1, 1]]

I have made reference in the comments to the question by FreshApple where a (slight variant) of the following method may be found:

InputForm[plot][[1, 1, 1]]

The following evaluates to True

plot[[1, 1]] == Cases[Normal@plot, Line[{x__}] :> x, Infinity] == 
 InputForm[plot][[1, 1, 1]] == Cases[Normal@plot, _Line, -1][[1, 1]]

Edit 3

Just or fun ...

ListPlot@ContourPlot[x^2 + y^2 == 1, {x, -1, 1}, {y, -1, 1}][[1, 1]]

gives

enter image description here

Community
  • 1
  • 1
681234
  • 4,214
  • 2
  • 35
  • 42
  • 2
    Nice. I remembered seeing something like this here at SO, but just could not remember how. Searching SO is so hard, too bad, because there are good information here, but hard to find and search. – Nasser Sep 09 '11 at 09:57
  • @Nasser. Yes, you are right about that. I have added a couple of links (to essentially the same question) and I suspect there are others. – 681234 Sep 09 '11 at 10:37
  • See [this](http://stackoverflow.com/q/7369439/499167) question by FreshApple for a very neat method using `Part` and `InputForm`. It seems to me that this is a much better method than those suggested above. I have asked FreshApple to consider posting an answer – 681234 Sep 10 '11 at 04:53
3

A $.02 contribution on Verbeia's answer:

Remember to check both x(y) and y(x) solutions as one of them could be cleaner than the other.

In your example:

enter image description here

Dr. belisarius
  • 60,527
  • 15
  • 115
  • 190
  • Thank you very much. Some equations can not use Solve、 NSolve to solution. Such as： Solve[E^(-(1/20) (-50 + y)^2) y - y Erf[125 - 9 y] + x y Erf[50 - 9 x y] == 0, {x}] NSolve[E^(-(1/20) (-50 + y)^2) y - y Erf[125 - 9 y] + x y Erf[50 - 9 x y] == 0, {x}] – h02h001 Sep 09 '11 at 13:54
  • @belisarius (Unrelated to the answer), the mma room has been frozen. Could you unfreeze it? – abcd Sep 09 '11 at 14:14
  • @yoda No AFAIK : http://meta.stackexchange.com/questions/97432/is-it-possible-for-the-owner-of-a-chat-room-that-has-been-frozen-to-edit-or-dele – Dr. belisarius Sep 09 '11 at 14:24
  • @belisarius Got it unfrozen :) We need to increase activity, lest it gets frozen again. – abcd Sep 09 '11 at 15:45