Python Tkinter mandelbrot set more accurate than c without a clear explanation

Question

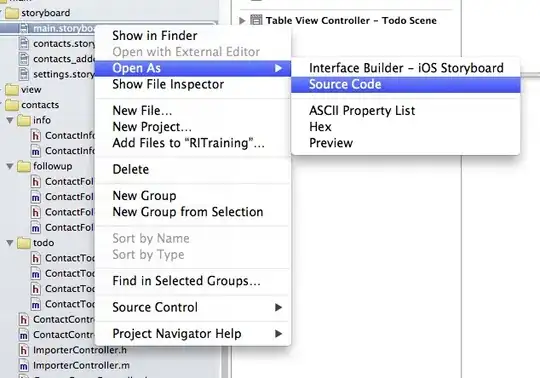
The following code draws a Mandelbrot set using Tkinter's Photo image format , using 256 iterations and a 256 color custom palette.

If you run it it displays a beautiful image with long smoky filaments and no concentric boundaries between iteration limits.

If I try to reproduce the code in c with the same limits and accuracy i got short filaments and concentric boundaries between iteration escape values.

The question is, what I am missing? What does Python behind my back to get more accuracy?

The left attached image is Python's

    # by Antoni Gual Via 4/2015

from tkinter import Tk, Canvas, PhotoImage,NW,mainloop 
from time import time

def mandel_pixel(c):   #c is a complex
  """ calculates the color index of the mandelbrot plane point passed in the arguments """
  maxIt = 256
  z =  c   
  for i in range(maxIt):
      a = z * z
      z=a + c  
      if a.real  > 4.:
         return i
      
  return maxIt

def mandelbrot(xa,xb,ya,yb,x,y):
    """ returns a mandelbrot in a string for Tk PhotoImage"""
    #color string table in Photoimage format #RRGGBB 
    clr=[ ' #%02x%02x%02x' % (int(255*((i/255)**.25)),0,0) for i in range(256)]
    clr.append(' #000000')  #append the color of the centre as index 256
    #calculate mandelbrot x,y coordinates for each screen pixel
    xm=list([xa + (xb - xa) * kx /x  for kx in range(x)])
    ym=list([ya + (yb - ya) * ky /y  for ky in range(y)])
    #build the Photoimage string by calling mandel_pixel to index in the color table
    return " ".join((("{"+"".join(clr[mandel_pixel(complex(i,j))] for i in xm))+"}" for j in ym))



#window size
x=640
y=480
#corners of  the complex plane to display  
xa = -2.0; xb = 1.0
ya = -1.27; yb = 1.27

#Tkinter window
window = Tk()
canvas = Canvas(window, width = x, height = y, bg = "#000000");canvas.pack()
img = PhotoImage(width = x, height = y)
canvas.create_image((0, 0), image = img, state = "normal", anchor = NW)

#do the mandelbrot
print('Starting Mandelbrot')
t1=time()
img.put(mandelbrot(xa,xb,ya,yb,x,y))
print(time()-t1, ' seconds')

mainloop()

And there is the relevant part of C code

int mandel(double x0,double y0, int maxit){
  double x=x0,  xt=0.;
  double y=y0; 
  int i;
  for (i=1;((x*x+y*y)<4.) && (i<=maxit);i++){
   xt=x*x-y*y+x0;
   y=2.*x*y+y0;
   x=xt ;   
  } 
  return(i<maxit ? rgb(255.*(pow(((double)i/maxit),.25)),0,0):0);
}

It came to me: perhaps I'm not using correctly the PhotoImage format and the long filaments are just artifacts? Perhaps the C version is the correct image? — Antoni Gual Via, Jul 09 '23 at 07:00

Spektre · Accepted Answer · 2023-07-09T08:53:31.723

I newer saw such filaments in mandelrot so my bet is the question should be what is wrong with the python code instead ...

even if you add fractional escape which adds much more details there are no such filaments also in approximations of interior distance / SDF does not have anything like that ... btw. I recently saw a question title here which complains about python pow ** operator and wrong complex domain result from real input it might be related but I never read it as I dislike Python to the core so I ignore that Q immediately.

However my bet is the problem lies in the complex power of python accuracy. Beacuse the complex domain pow is calculated like this:

vec2 cpow(vec2 a,vec2 b)    // a^b
    {
    return cexp(cmul(cln(a),b));
    }

taken from How to express tetration function, for complex numbers for another fractal of this family of fractals...

which adds much more rounding than simple multiply add substract for integer exponents...

So once you iterate many times the rounding error will became more nad more dominant so what you consider added details is accuracy error instead.

My bet is if you rewrite python code to not use pow ** operator then the result will be the same (which would confirm my conclusions).

Spektre: You were right. Removing the use of complex objects in the iteration made the artifacts go away. Even if i was just multiplying a complex by itself to get the square, to avoid using pow.... — Antoni Gual Via, Jul 09 '23 at 11:46
@AntoniGualVia complex domain operations on small magnitude numbers along with FPU rounding errors can sometime produce volatile noise in scale much much beond naive instinctive expectations from real domain experience. — Spektre, Jul 09 '23 at 11:53
If you write a product of a value by itself in a formula you expect the interpreter will not be using pow() behind your back.... — Antoni Gual Via, Jul 09 '23 at 12:43

Python Tkinter mandelbrot set more accurate than c without a clear explanation

1 Answers1