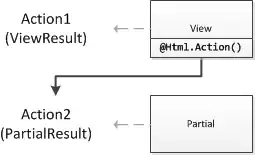
This is really easy, all you have to do is find the perpendicular (abbr here |_) distance from the point P to the plane, then translate P back by the perpendicular distance in the direction of the plane normal. The result is the translated P sits in the plane.
Taking an easy example (that we can verify by inspection) :
Set n=(0,1,0), and P=(10,20,-5).
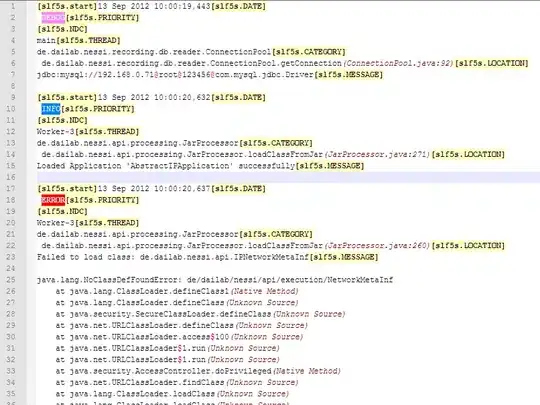
The projected point should be (10,10,-5). You can see by inspection that Pproj is 10 units perpendicular from the plane, and if it were in the plane, it would have y=10.
So how do we find this analytically?
The plane equation is Ax+By+Cz+d=0. What this equation means is "in order for a point (x,y,z) to be in the plane, it must satisfy Ax+By+Cz+d=0".
What is the Ax+By+Cz+d=0 equation for the plane drawn above?
The plane has normal n=(0,1,0). The d is found simply by using a test point already in the plane:
(0)x + (1)y + (0)z + d = 0
The point (0,10,0) is in the plane. Plugging in above, we find, d=-10. The plane equation is then 0x + 1y + 0z - 10 = 0 (if you simplify, you get y=10).
A nice interpretation of d is it speaks of the perpendicular distance you would need to translate the plane along its normal to have the plane pass through the origin.
Anyway, once we have d, we can find the |_ distance of any point to the plane by the following equation:

There are 3 possible classes of results for |_ distance to plane:
- 0: ON PLANE EXACTLY (almost never happens with floating point inaccuracy issues)
- +1: >0: IN FRONT of plane (on normal side)
- -1: <0: BEHIND plane (ON OPPOSITE SIDE OF NORMAL)
Anyway,
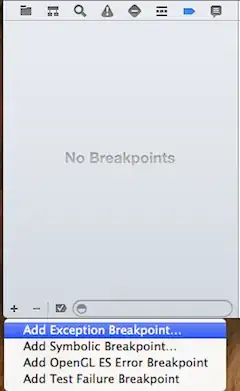
Which you can verify as correct by inspection in the diagram above