function pointCircleCollide(point, circle, r) {
if (r===0) return false
var dx = circle[0] - point[0]
var dy = circle[1] - point[1]
return dx * dx + dy * dy <= r * r
}
var tmp = [0, 0]
function lineCircleCollide(a, b, circle, radius, nearest) {
//check to see if start or end points lie within circle
if (pointCircleCollide(a, circle, radius)) {
if (nearest) {
nearest[0] = a[0]
nearest[1] = a[1]
}
return true
} if (pointCircleCollide(b, circle, radius)) {
if (nearest) {
nearest[0] = b[0]
nearest[1] = b[1]
}
return true
}
var x1 = a[0],
y1 = a[1],
x2 = b[0],
y2 = b[1],
cx = circle[0],
cy = circle[1]
//vector d
var dx = x2 - x1
var dy = y2 - y1
//vector lc
var lcx = cx - x1
var lcy = cy - y1
//project lc onto d, resulting in vector p
var dLen2 = dx * dx + dy * dy //len2 of d
var px = dx
var py = dy
if (dLen2 > 0) {
var dp = (lcx * dx + lcy * dy) / dLen2
px *= dp
py *= dp
}
if (!nearest)
nearest = tmp
nearest[0] = x1 + px
nearest[1] = y1 + py
//len2 of p
var pLen2 = px * px + py * py
//check collision
return pointCircleCollide(nearest, circle, radius)
&& pLen2 <= dLen2 && (px * dx + py * dy) >= 0
}
var circle = [5, 5],
radius = 25,
a = [5, 6],
b = [10, 10]
var hit = lineCircleCollide(a, b, circle, radius)
 This is the basic concept if you don't know how to solve equations in general. I will leave the rest of the thinking to you. ;) Figuring out
This is the basic concept if you don't know how to solve equations in general. I will leave the rest of the thinking to you. ;) Figuring out 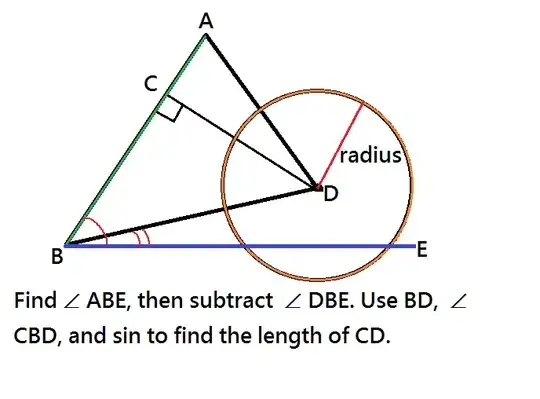 Finding collisions in JavaScript is kind of complicated.
Finding collisions in JavaScript is kind of complicated.