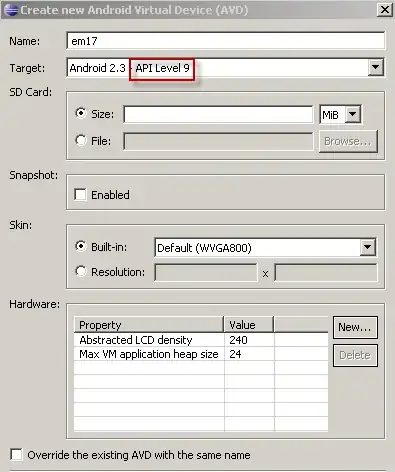
This is a homework problem which I tried to solve by myself but I couldn't. The homework is to implement a circuit that multiplies two binary numbers by using right shifting. I don't have any problems with Verilog, my only problem is how to conclude the algorithm so I can implement it by myself.
Asked
Active
Viewed 2,972 times
0
-
The algorithm will become obvious when you do a manual written binary multiplication of two numbers – Stefan Haustein Dec 06 '16 at 18:30
-
@StefanHaustein Manual written binary multiplication uses left-shifting, the requirement is to use right shifting as shown in the figure. – Ambitions Dec 06 '16 at 18:35
-
The product goes into the high 32 bit of the 64 bit word, so you basically just start with implied << 32, then << 31 etc. – Stefan Haustein Dec 06 '16 at 19:06
-
@rcgldr This is an unsigned multiply. The multiplier will be the least significant bits. – Ambitions Dec 06 '16 at 21:20
-
@Ambitions - deleted my prior comment. The right shifting of both product and multiplier in the same register should not be an issue, as noted by Stefan Haustein. I'm still wondering about the carry from adds, where is the carry output from the 32 bit ALU? Assuming the ALU outputs a 33 bit sum (includes the carry bit), then shift product / multiplier right 1 bit, and if a 1 bit was shifted out of multiplier, add multiplicand starting at bit 31 (not bit 32) of the product / multiplier register. – rcgldr Dec 06 '16 at 22:27
-
@rcgldr I tried to do right shifting with addition for 0101 * 1100, and this is what I have got: 00001100 -> 00000110 -> 00000011 -> 10101001 -> 11111100 which is wrong of course. I did what you have said even before reading your comment but it was useless, or maybe I did it wrong. Could you please explain how to do it for 0101 * 1100? – Ambitions Dec 07 '16 at 06:43
1 Answers
2
Example multiplies. Note 4 bit adder produces a 5 bit sum (top bit is carry). Input to adder is multiplicand plus bits 3 to 6 of product register, the sum including carry, goes to bits 3 to 7 of product register.
multiplicand 1100, multiplier 0101
7 6 5 4 3 2 1 0 product bit index
0 0 0 0 0 1 0 1 initial 8 bit register
0 0 0 0 0 0 1 0 1 shift right, 1 bit shifted out
1 1 0 0 add multiplicand
0 1 1 0 0 0 1 0
0 0 1 1 0 0 0 1 0 shift right, 0 bit shifted out
0 0 0 0 no add
0 0 1 1 0 0 0 1
0 0 0 1 1 0 0 0 1 shift right, 1 bit shifted out
1 1 0 0 add multiplicand
0 1 1 1 1 0 0 0
0 0 1 1 1 1 0 0 0 shift right, 0 bit shifted out
0 0 0 0 no add
0 0 1 1 1 1 0 0
multiplicand 1111, multiplier 1111
0 0 0 0 1 1 1 1 initial 8 bit register
0 0 0 0 0 1 1 1 1 shift right, 1 bit shifted out
1 1 1 1 add multiplicand
0 1 1 1 1 1 1 1
0 0 1 1 1 1 1 1 1 shift right, 1 bit shifted out
1 1 1 1 add multiplicand
1 0 1 1 0 1 1 1
0 1 0 1 1 0 1 1 1 shift right, 1 bit shifted out
1 1 1 1 add multiplicand
1 1 0 1 0 0 1 1
0 1 1 0 1 0 0 1 1 shift right, 1 bit shifted out
1 1 1 1 add multiplicand
1 1 1 0 0 0 0 1
rcgldr
- 27,407
- 3
- 36
- 61