-1
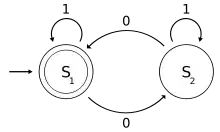
module multiplication (multiplier, multiplicand, product, clk);

input [3:0] multiplier;
input [4:0] multiplicand;
input clk;
output [7:0] product;
reg [7:0] product;

initial
begin
    product [7:4] = 4'b0000;
    product [3:0] = 4'b1100;
end

always @ (posedge clk)
begin
    if (product[0] == 1)
    begin
        product <= product >> 1;
        product[7:3] <= product[7:3] + multiplicand[4:0];
    end
    else
    begin
        product <= product >> 1;
    end
end

endmodule

This verilog code is to implement the circuit mentioned in this question: How to perform right shifting binary multiplication?, the waveform is correct until the last step. The correct answer should be 00111100

Waveform: Waveform

Community
  • 1
  • 1
Ambitions
  • 2,369
  • 3
  • 13
  • 24

1 Answers1

0

Why would it be?

We know at t=300ns, product[0]==1, so we're using the first option of the if-else. In that case, we have the following:

    product <= product >> 1;
    product[7:3] <= product[7:3] + multiplicand[4:0];

Because you're (correctly) using non-blocking assignments, the value of product isn't updated until the always block completes. That means the second assignment uses the unshifted value of product. We could simplify this expression as

    product[2:0] <= product [3:1];
    product[7:3] <= product[7:3] + multiplicand[4:0];

and the result would be the same.

The first statement give us 0b100. The second gives us 0b00101 + 0b00101 = 0b01010. In total, this produces 0b01010100, which matches the simulation output.

wilcroft
  • 1,580
  • 2
  • 14
  • 20
  • That may be. My point was that the problem isn't with the simulator, but with your algorithm and/or implementation. The output of the simulator matches the code you've written. – wilcroft Dec 09 '16 at 21:30
  • One fix could be to replace the assignment in the first half of the if-else with `product = {product[7:3] + multiplicand[4:0], product [2:1], 1'b0};`, in order to add a cycle for the addition. (i.e. shift->shift->add->shift->add). You would set bit [0] to 0 to indicate that you've done the addition for that stage. – wilcroft Dec 09 '16 at 21:34