How can I determine whether a 2D Point is within a Polygon?

Question

I'm trying to create a fast 2D point inside polygon algorithm, for use in hit-testing (e.g. Polygon.contains(p:Point)). Suggestions for effective techniques would be appreciated.

Answer 1

For graphics, I'd rather not prefer integers. Many systems use integers for UI painting (pixels are ints after all), but macOS, for example, uses float for everything. macOS only knows points and a point can translate to one pixel, but depending on monitor resolution, it might translate to something else. On retina screens half a point (0.5/0.5) is pixel. Still, I never noticed that macOS UIs are significantly slower than other UIs. After all, 3D APIs (OpenGL or Direct3D) also work with floats and modern graphics libraries very often take advantage of GPU acceleration.

Now you said speed is your main concern, okay, let's go for speed. Before you run any sophisticated algorithm, first do a simple test. Create an axis aligned bounding box around your polygon. This is very easy, fast and can already save you a lot of calculations. How does that work? Iterate over all points of the polygon and find the min/max values of X and Y.

E.g. you have the points (9/1), (4/3), (2/7), (8/2), (3/6). This means Xmin is 2, Xmax is 9, Ymin is 1 and Ymax is 7. A point outside of the rectangle with the two edges (2/1) and (9/7) cannot be within the polygon.

// p is your point, p.x is the x coord, p.y is the y coord
if (p.x < Xmin || p.x > Xmax || p.y < Ymin || p.y > Ymax) {
    // Definitely not within the polygon!
}

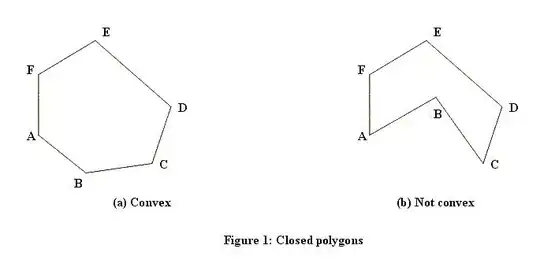
This is the first test to run for any point. As you can see, this test is ultra fast but it's also very coarse. To handle points that are within the bounding rectangle, we need a more sophisticated algorithm. There are a couple of ways how this can be calculated. Which method works also depends on whether the polygon can have holes or will always be solid. Here are examples of solid ones (one convex, one concave):

And here's one with a hole:

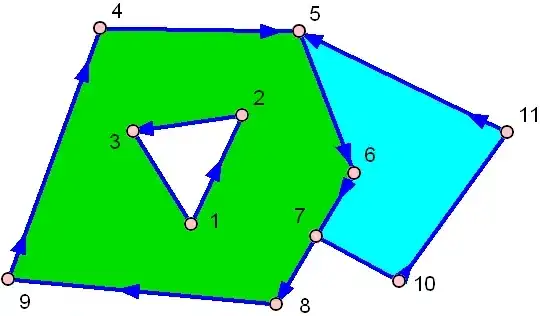
The green one has a hole in the middle!

The easiest algorithm, that can handle all three cases above and is still pretty fast is named ray casting. The idea of the algorithm is pretty simple: Draw a virtual ray from anywhere outside the polygon to your point and count how often it hits a side of the polygon. If the number of hits is even, it's outside of the polygon, if it's odd, it's inside.

The winding number algorithm would be an alternative, it is more accurate for points being very close to a polygon line but it's also much slower. Ray casting may fail for points too close to a polygon side because of limited floating point precision and rounding issues, but in reality that is hardly a problem, as if a point lies that close to a side, it's often visually not even possible for a viewer to recognize if it is already inside or still outside.

You still have the bounding box of above, remember? Just pick a point outside the bounding box and use it as starting point for your ray. E.g. the point (Xmin - e/p.y) is outside the polygon for sure.

But what is e? Well, e (actually epsilon) gives the bounding box some padding. As I said, ray tracing fails if we start too close to a polygon line. Since the bounding box might equal the polygon (if the polygon is an axis aligned rectangle, the bounding box is equal to the polygon itself!), we need some padding to make this safe, that's all. How big should you choose e? Not too big. It depends on the coordinate system scale you use for drawing. If your pixel step width is 1.0, then just choose 1.0 (yet 0.1 would have worked as well)

Now that we have the ray with its start and end coordinates, the problem shifts from "is the point within the polygon" to "how often does the ray intersects a polygon side". Therefore we can't just work with the polygon points as before, now we need the actual sides. A side is always defined by two points.

side 1: (X1/Y1)-(X2/Y2)
side 2: (X2/Y2)-(X3/Y3)
side 3: (X3/Y3)-(X4/Y4)
:

You need to test the ray against all sides. Consider the ray to be a vector and every side to be a vector. The ray has to hit each side exactly once or never at all. It can't hit the same side twice. Two lines in 2D space will always intersect exactly once, unless they are parallel, in which case they never intersect. However since vectors have a limited length, two vectors might not be parallel and still never intersect because they are too short to ever meet each other.

// Test the ray against all sides
int intersections = 0;
for (side = 0; side < numberOfSides; side++) {
    // Test if current side intersects with ray.
    // If yes, intersections++;
}
if ((intersections & 1) == 1) {
    // Inside of polygon
} else {
    // Outside of polygon
}

So far so well, but how do you test if two vectors intersect? Here's some C code (not tested), that should do the trick:

#define NO 0
#define YES 1
#define COLLINEAR 2

int areIntersecting(
    float v1x1, float v1y1, float v1x2, float v1y2,
    float v2x1, float v2y1, float v2x2, float v2y2
) {
    float d1, d2;
    float a1, a2, b1, b2, c1, c2;

    // Convert vector 1 to a line (line 1) of infinite length.
    // We want the line in linear equation standard form: A*x + B*y + C = 0
    // See: http://en.wikipedia.org/wiki/Linear_equation
    a1 = v1y2 - v1y1;
    b1 = v1x1 - v1x2;
    c1 = (v1x2 * v1y1) - (v1x1 * v1y2);

    // Every point (x,y), that solves the equation above, is on the line,
    // every point that does not solve it, is not. The equation will have a
    // positive result if it is on one side of the line and a negative one 
    // if is on the other side of it. We insert (x1,y1) and (x2,y2) of vector
    // 2 into the equation above.
    d1 = (a1 * v2x1) + (b1 * v2y1) + c1;
    d2 = (a1 * v2x2) + (b1 * v2y2) + c1;

    // If d1 and d2 both have the same sign, they are both on the same side
    // of our line 1 and in that case no intersection is possible. Careful, 
    // 0 is a special case, that's why we don't test ">=" and "<=", 
    // but "<" and ">".
    if (d1 > 0 && d2 > 0) return NO;
    if (d1 < 0 && d2 < 0) return NO;

    // The fact that vector 2 intersected the infinite line 1 above doesn't 
    // mean it also intersects the vector 1. Vector 1 is only a subset of that
    // infinite line 1, so it may have intersected that line before the vector
    // started or after it ended. To know for sure, we have to repeat the
    // the same test the other way round. We start by calculating the 
    // infinite line 2 in linear equation standard form.
    a2 = v2y2 - v2y1;
    b2 = v2x1 - v2x2;
    c2 = (v2x2 * v2y1) - (v2x1 * v2y2);

    // Calculate d1 and d2 again, this time using points of vector 1.
    d1 = (a2 * v1x1) + (b2 * v1y1) + c2;
    d2 = (a2 * v1x2) + (b2 * v1y2) + c2;

    // Again, if both have the same sign (and neither one is 0),
    // no intersection is possible.
    if (d1 > 0 && d2 > 0) return NO;
    if (d1 < 0 && d2 < 0) return NO;

    // If we get here, only two possibilities are left. Either the two
    // vectors intersect in exactly one point or they are collinear, which
    // means they intersect in any number of points from zero to infinite.
    if ((a1 * b2) - (a2 * b1) == 0.0f) return COLLINEAR;

    // If they are not collinear, they must intersect in exactly one point.
    return YES;
}

The input values are the two endpoints of vector 1 (v1x1/v1y1 and v1x2/v1y2) and vector 2 (v2x1/v2y1 and v2x2/v2y2). So you have 2 vectors, 4 points, 8 coordinates. YES and NO are clear. YES increases intersections, NO does nothing.

What about COLLINEAR? It means both vectors lie on the same infinite line, depending on position and length, they don't intersect at all or they intersect in an endless number of points. I'm not absolutely sure how to handle this case, I would not count it as intersection either way. Well, this case is rather rare in practice anyway because of floating point rounding errors; better code would probably not test for == 0.0f but instead for something like < epsilon, where epsilon is a rather small number.

If you need to test a larger number of points, you can certainly speed up the whole thing a bit by keeping the linear equation standard forms of the polygon sides in memory, so you don't have to recalculate these every time. This will save you two floating point multiplications and three floating point subtractions on every test in exchange for storing three floating point values per polygon side in memory. It's a typical memory vs computation time trade off.

Last but not least: If you may use 3D hardware to solve the problem, there is an interesting alternative. Just let the GPU do all the work for you. Create a painting surface that is off screen. Fill it completely with the color black. Now let OpenGL or Direct3D paint your polygon (or even all of your polygons if you just want to test if the point is within any of them, but you don't care for which one) and fill the polygon(s) with a different color, e.g. white. To check if a point is within the polygon, get the color of this point from the drawing surface. This is just a O(1) memory fetch.

Of course this method is only usable if your drawing surface doesn't have to be huge. If it cannot fit into the GPU memory, this method is slower than doing it on the CPU. If it would have to be huge and your GPU supports modern shaders, you can still use the GPU by implementing the ray casting shown above as a GPU shader, which absolutely is possible. For a larger number of polygons or a large number of points to test, this will pay off, consider some GPUs will be able to test 64 to 256 points in parallel. Note however that transferring data from CPU to GPU and back is always expensive, so for just testing a couple of points against a couple of simple polygons, where either the points or the polygons are dynamic and will change frequently, a GPU approach will rarely pay off.

Answer 2

I think the following piece of code is the best solution (taken from here):

int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy)
{
  int i, j, c = 0;
  for (i = 0, j = nvert-1; i < nvert; j = i++) {
    if ( ((verty[i]>testy) != (verty[j]>testy)) &&
     (testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )
       c = !c;
  }
  return c;
}

Arguments

• nvert: Number of vertices in the polygon. Whether to repeat the first vertex at the end has been discussed in the article referred above.
• vertx, verty: Arrays containing the x- and y-coordinates of the polygon's vertices.
• testx, testy: X- and y-coordinate of the test point.

It's both short and efficient and works both for convex and concave polygons. As suggested before, you should check the bounding rectangle first and treat polygon holes separately.

The idea behind this is pretty simple. The author describes it as follows:

I run a semi-infinite ray horizontally (increasing x, fixed y) out from the test point, and count how many edges it crosses. At each crossing, the ray switches between inside and outside. This is called the Jordan curve theorem.

The variable c is switching from 0 to 1 and 1 to 0 each time the horizontal ray crosses any edge. So basically it's keeping track of whether the number of edges crossed are even or odd. 0 means even and 1 means odd.

Answer 3

Here is a C# version of the answer given by nirg, which comes from this RPI professor. Note that use of the code from that RPI source requires attribution.

A bounding box check has been added at the top. However, as James Brown points out, the main code is almost as fast as the bounding box check itself, so the bounding box check can actually slow the overall operation, in the case that most of the points you are checking are inside the bounding box. So you could leave the bounding box check out, or an alternative would be to precompute the bounding boxes of your polygons if they don't change shape too often.

public bool IsPointInPolygon( Point p, Point[] polygon )
{
    double minX = polygon[ 0 ].X;
    double maxX = polygon[ 0 ].X;
    double minY = polygon[ 0 ].Y;
    double maxY = polygon[ 0 ].Y;
    for ( int i = 1 ; i < polygon.Length ; i++ )
    {
        Point q = polygon[ i ];
        minX = Math.Min( q.X, minX );
        maxX = Math.Max( q.X, maxX );
        minY = Math.Min( q.Y, minY );
        maxY = Math.Max( q.Y, maxY );
    }

    if ( p.X < minX || p.X > maxX || p.Y < minY || p.Y > maxY )
    {
        return false;
    }

    // https://wrf.ecse.rpi.edu/Research/Short_Notes/pnpoly.html
    bool inside = false;
    for ( int i = 0, j = polygon.Length - 1 ; i < polygon.Length ; j = i++ )
    {
        if ( ( polygon[ i ].Y > p.Y ) != ( polygon[ j ].Y > p.Y ) &&
             p.X < ( polygon[ j ].X - polygon[ i ].X ) * ( p.Y - polygon[ i ].Y ) / ( polygon[ j ].Y - polygon[ i ].Y ) + polygon[ i ].X )
        {
            inside = !inside;
        }
    }

    return inside;
}

Answer 4

Here is a JavaScript variant of the answer by M. Katz based on Nirg's approach:

function pointIsInPoly(p, polygon) {
    var isInside = false;
    var minX = polygon[0].x, maxX = polygon[0].x;
    var minY = polygon[0].y, maxY = polygon[0].y;
    for (var n = 1; n < polygon.length; n++) {
        var q = polygon[n];
        minX = Math.min(q.x, minX);
        maxX = Math.max(q.x, maxX);
        minY = Math.min(q.y, minY);
        maxY = Math.max(q.y, maxY);
    }

    if (p.x < minX || p.x > maxX || p.y < minY || p.y > maxY) {
        return false;
    }

    var i = 0, j = polygon.length - 1;
    for (i, j; i < polygon.length; j = i++) {
        if ( (polygon[i].y > p.y) != (polygon[j].y > p.y) &&
                p.x < (polygon[j].x - polygon[i].x) * (p.y - polygon[i].y) / (polygon[j].y - polygon[i].y) + polygon[i].x ) {
            isInside = !isInside;
        }
    }

    return isInside;
}

Answer 5

Compute the oriented sum of angles between the point p and each of the polygon apices. If the total oriented angle is 360 degrees, the point is inside. If the total is 0, the point is outside.

I like this method better because it is more robust and less dependent on numerical precision.

Methods that compute evenness of number of intersections are limited because you can 'hit' an apex during the computation of the number of intersections.

EDIT: By The Way, this method works with concave and convex polygons.

EDIT: I recently found a whole Wikipedia article on the topic.

Answer 6

This question is so interesting. I have another workable idea different from other answers to this post. The idea is to use the sum of angles to decide whether the target is inside or outside. Better known as winding number.

Let x be the target point. Let array [0, 1, .... n] be the all the points of the area. Connect the target point with every border point with a line. If the target point is inside of this area. The sum of all angles will be 360 degrees. If not the angles will be less than 360.

Refer to this image to get a basic understanding of the idea:

My algorithm assumes the clockwise is the positive direction. Here is a potential input:

[[-122.402015, 48.225216], [-117.032049, 48.999931], [-116.919132, 45.995175], [-124.079107, 46.267259], [-124.717175, 48.377557], [-122.92315, 47.047963], [-122.402015, 48.225216]]

The following is the python code that implements the idea:

def isInside(self, border, target):
degree = 0
for i in range(len(border) - 1):
    a = border[i]
    b = border[i + 1]

    # calculate distance of vector
    A = getDistance(a[0], a[1], b[0], b[1]);
    B = getDistance(target[0], target[1], a[0], a[1])
    C = getDistance(target[0], target[1], b[0], b[1])

    # calculate direction of vector
    ta_x = a[0] - target[0]
    ta_y = a[1] - target[1]
    tb_x = b[0] - target[0]
    tb_y = b[1] - target[1]

    cross = tb_y * ta_x - tb_x * ta_y
    clockwise = cross < 0

    # calculate sum of angles
    if(clockwise):
        degree = degree + math.degrees(math.acos((B * B + C * C - A * A) / (2.0 * B * C)))
    else:
        degree = degree - math.degrees(math.acos((B * B + C * C - A * A) / (2.0 * B * C)))

if(abs(round(degree) - 360) <= 3):
    return True
return False

Answer 7

The Eric Haines article cited by bobobobo is really excellent. Particularly interesting are the tables comparing performance of the algorithms; the angle summation method is really bad compared to the others. Also interesting is that optimisations like using a lookup grid to further subdivide the polygon into "in" and "out" sectors can make the test incredibly fast even on polygons with > 1000 sides.

Anyway, it's early days but my vote goes to the "crossings" method, which is pretty much what Mecki describes I think. However I found it most succintly described and codified by David Bourke. I love that there is no real trigonometry required, and it works for convex and concave, and it performs reasonably well as the number of sides increases.

By the way, here's one of the performance tables from the Eric Haines' article for interest, testing on random polygons.

                       number of edges per polygon
                         3       4      10      100    1000
MacMartin               2.9     3.2     5.9     50.6    485
Crossings               3.1     3.4     6.8     60.0    624
Triangle Fan+edge sort  1.1     1.8     6.5     77.6    787
Triangle Fan            1.2     2.1     7.3     85.4    865
Barycentric             2.1     3.8    13.8    160.7   1665
Angle Summation        56.2    70.4   153.6   1403.8  14693

Grid (100x100)          1.5     1.5     1.6      2.1      9.8
Grid (20x20)            1.7     1.7     1.9      5.7     42.2
Bins (100)              1.8     1.9     2.7     15.1    117
Bins (20)               2.1     2.2     3.7     26.3    278

Answer 8

Really like the solution posted by Nirg and edited by bobobobo. I just made it javascript friendly and a little more legible for my use:

function insidePoly(poly, pointx, pointy) {
    var i, j;
    var inside = false;
    for (i = 0, j = poly.length - 1; i < poly.length; j = i++) {
        if(((poly[i].y > pointy) != (poly[j].y > pointy)) && (pointx < (poly[j].x-poly[i].x) * (pointy-poly[i].y) / (poly[j].y-poly[i].y) + poly[i].x) ) inside = !inside;
    }
    return inside;
}

Answer 9

Swift version of the answer by nirg:

extension CGPoint {
    func isInsidePolygon(vertices: [CGPoint]) -> Bool {
        guard !vertices.isEmpty else { return false }
        var j = vertices.last!, c = false
        for i in vertices {
            let a = (i.y > y) != (j.y > y)
            let b = (x < (j.x - i.x) * (y - i.y) / (j.y - i.y) + i.x)
            if a && b { c = !c }
            j = i
        }
        return c
    }
}

Answer 10

Most of the answers in this question are not handling all corner cases well. Some subtle corner cases like below: This is a javascript version with all corner cases well handled.

/** Get relationship between a point and a polygon using ray-casting algorithm
 * @param {{x:number, y:number}} P: point to check
 * @param {{x:number, y:number}[]} polygon: the polygon
 * @returns -1: outside, 0: on edge, 1: inside
 */
function relationPP(P, polygon) {
    const between = (p, a, b) => p >= a && p <= b || p <= a && p >= b
    let inside = false
    for (let i = polygon.length-1, j = 0; j < polygon.length; i = j, j++) {
        const A = polygon[i]
        const B = polygon[j]
        // corner cases
        if (P.x == A.x && P.y == A.y || P.x == B.x && P.y == B.y) return 0
        if (A.y == B.y && P.y == A.y && between(P.x, A.x, B.x)) return 0

        if (between(P.y, A.y, B.y)) { // if P inside the vertical range
            // filter out "ray pass vertex" problem by treating the line a little lower
            if (P.y == A.y && B.y >= A.y || P.y == B.y && A.y >= B.y) continue
            // calc cross product `PA X PB`, P lays on left side of AB if c > 0 
            const c = (A.x - P.x) * (B.y - P.y) - (B.x - P.x) * (A.y - P.y)
            if (c == 0) return 0
            if ((A.y < B.y) == (c > 0)) inside = !inside
        }
    }

    return inside? 1 : -1
}

Answer 11

I did some work on this back when I was a researcher under Michael Stonebraker - you know, the professor who came up with Ingres, PostgreSQL, etc.

We realized that the fastest way was to first do a bounding box because it's SUPER fast. If it's outside the bounding box, it's outside. Otherwise, you do the harder work...

If you want a great algorithm, look to the open source project PostgreSQL source code for the geo work...

I want to point out, we never got any insight into right vs left handedness (also expressible as an "inside" vs "outside" problem...

---

UPDATE

BKB's link provided a good number of reasonable algorithms. I was working on Earth Science problems and therefore needed a solution that works in latitude/longitude, and it has the peculiar problem of handedness - is the area inside the smaller area or the bigger area? The answer is that the "direction" of the verticies matters - it's either left-handed or right handed and in this way you can indicate either area as "inside" any given polygon. As such, my work used solution three enumerated on that page.

In addition, my work used separate functions for "on the line" tests.

...Since someone asked: we figured out that bounding box tests were best when the number of verticies went beyond some number - do a very quick test before doing the longer test if necessary... A bounding box is created by simply taking the largest x, smallest x, largest y and smallest y and putting them together to make four points of a box...

Another tip for those that follow: we did all our more sophisticated and "light-dimming" computing in a grid space all in positive points on a plane and then re-projected back into "real" longitude/latitude, thus avoiding possible errors of wrapping around when one crossed line 180 of longitude and when handling polar regions. Worked great!

Answer 12

Java Version:

public class Geocode {
    private float latitude;
    private float longitude;

    public Geocode() {
    }

    public Geocode(float latitude, float longitude) {
        this.latitude = latitude;
        this.longitude = longitude;
    }

    public float getLatitude() {
        return latitude;
    }

    public void setLatitude(float latitude) {
        this.latitude = latitude;
    }

    public float getLongitude() {
        return longitude;
    }

    public void setLongitude(float longitude) {
        this.longitude = longitude;
    }
}

public class GeoPolygon {
    private ArrayList<Geocode> points;

    public GeoPolygon() {
        this.points = new ArrayList<Geocode>();
    }

    public GeoPolygon(ArrayList<Geocode> points) {
        this.points = points;
    }

    public GeoPolygon add(Geocode geo) {
        points.add(geo);
        return this;
    }

    public boolean inside(Geocode geo) {
        int i, j;
        boolean c = false;
        for (i = 0, j = points.size() - 1; i < points.size(); j = i++) {
            if (((points.get(i).getLongitude() > geo.getLongitude()) != (points.get(j).getLongitude() > geo.getLongitude())) &&
                    (geo.getLatitude() < (points.get(j).getLatitude() - points.get(i).getLatitude()) * (geo.getLongitude() - points.get(i).getLongitude()) / (points.get(j).getLongitude() - points.get(i).getLongitude()) + points.get(i).getLatitude()))
                c = !c;
        }
        return c;
    }

}

Answer 13

The trivial solution would be to divide the polygon to triangles and hit test the triangles as explained here

If your polygon is CONVEX there might be a better approach though. Look at the polygon as a collection of infinite lines. Each line dividing space into two. for every point it's easy to say if its on the one side or the other side of the line. If a point is on the same side of all lines then it is inside the polygon.

Answer 14

David Segond's answer is pretty much the standard general answer, and Richard T's is the most common optimization, though therre are some others. Other strong optimizations are based on less general solutions. For example if you are going to check the same polygon with lots of points, triangulating the polygon can speed things up hugely as there are a number of very fast TIN searching algorithms. Another is if the polygon and points are on a limited plane at low resolution, say a screen display, you can paint the polygon onto a memory mapped display buffer in a given colour, and check the color of a given pixel to see if it lies in the polygons.

Like many optimizations, these are based on specific rather than general cases, and yield beneifits based on amortized time rather than single usage.

Working in this field, i found Joeseph O'Rourkes 'Computation Geometry in C' ISBN 0-521-44034-3 to be a great help.

Answer 15

Obj-C version of nirg's answer with sample method for testing points. Nirg's answer worked well for me.

- (BOOL)isPointInPolygon:(NSArray *)vertices point:(CGPoint)test {
    NSUInteger nvert = [vertices count];
    NSInteger i, j, c = 0;
    CGPoint verti, vertj;

    for (i = 0, j = nvert-1; i < nvert; j = i++) {
        verti = [(NSValue *)[vertices objectAtIndex:i] CGPointValue];
        vertj = [(NSValue *)[vertices objectAtIndex:j] CGPointValue];
        if (( (verti.y > test.y) != (vertj.y > test.y) ) &&
        ( test.x < ( vertj.x - verti.x ) * ( test.y - verti.y ) / ( vertj.y - verti.y ) + verti.x) )
            c = !c;
    }

    return (c ? YES : NO);
}

- (void)testPoint {

    NSArray *polygonVertices = [NSArray arrayWithObjects:
        [NSValue valueWithCGPoint:CGPointMake(13.5, 41.5)],
        [NSValue valueWithCGPoint:CGPointMake(42.5, 56.5)],
        [NSValue valueWithCGPoint:CGPointMake(39.5, 69.5)],
        [NSValue valueWithCGPoint:CGPointMake(42.5, 84.5)],
        [NSValue valueWithCGPoint:CGPointMake(13.5, 100.0)],
        [NSValue valueWithCGPoint:CGPointMake(6.0, 70.5)],
        nil
    ];

    CGPoint tappedPoint = CGPointMake(23.0, 70.0);

    if ([self isPointInPolygon:polygonVertices point:tappedPoint]) {
        NSLog(@"YES");
    } else {
        NSLog(@"NO");
    }
}

Answer 16

There is nothing more beutiful than an inductive definition of a problem. For the sake of completeness here you have a version in prolog which might also clarify the thoughs behind ray casting:

Based on the simulation of simplicity algorithm in http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html

Some helper predicates:

exor(A,B):- \+A,B;A,\+B.
in_range(Coordinate,CA,CB) :- exor((CA>Coordinate),(CB>Coordinate)).

inside(false).
inside(_,[_|[]]).
inside(X:Y, [X1:Y1,X2:Y2|R]) :- in_range(Y,Y1,Y2), X > ( ((X2-X1)*(Y-Y1))/(Y2-Y1) +      X1),toggle_ray, inside(X:Y, [X2:Y2|R]); inside(X:Y, [X2:Y2|R]).

get_line(_,_,[]).
get_line([XA:YA,XB:YB],[X1:Y1,X2:Y2|R]):- [XA:YA,XB:YB]=[X1:Y1,X2:Y2]; get_line([XA:YA,XB:YB],[X2:Y2|R]).

The equation of a line given 2 points A and B (Line(A,B)) is:

                    (YB-YA)
           Y - YA = ------- * (X - XA) 
                    (XB-YB) 

It is important that the direction of rotation for the line is setted to clock-wise for boundaries and anti-clock-wise for holes. We are going to check whether the point (X,Y), i.e the tested point is at the left half-plane of our line (it is a matter of taste, it could also be the right side, but also the direction of boundaries lines has to be changed in that case), this is to project the ray from the point to the right (or left) and acknowledge the intersection with the line. We have chosen to project the ray in the horizontal direction (again it is a matter of taste, it could also be done in vertical with similar restrictions), so we have:

               (XB-XA)
           X < ------- * (Y - YA) + XA
               (YB-YA) 

Now we need to know if the point is at the left (or right) side of the line segment only, not the entire plane, so we need to restrict the search only to this segment, but this is easy since to be inside the segment only one point in the line can be higher than Y in the vertical axis. As this is a stronger restriction it needs to be the first to check, so we take first only those lines meeting this requirement and then check its possition. By the Jordan Curve theorem any ray projected to a polygon must intersect at an even number of lines. So we are done, we will throw the ray to the right and then everytime it intersects a line, toggle its state. However in our implementation we are goint to check the lenght of the bag of solutions meeting the given restrictions and decide the innership upon it. for each line in the polygon this have to be done.

is_left_half_plane(_,[],[],_).
is_left_half_plane(X:Y,[XA:YA,XB:YB], [[X1:Y1,X2:Y2]|R], Test) :- [XA:YA, XB:YB] =  [X1:Y1, X2:Y2], call(Test, X , (((XB - XA) * (Y - YA)) / (YB - YA) + XA)); 
                                                        is_left_half_plane(X:Y, [XA:YA, XB:YB], R, Test).

in_y_range_at_poly(Y,[XA:YA,XB:YB],Polygon) :- get_line([XA:YA,XB:YB],Polygon),  in_range(Y,YA,YB).
all_in_range(Coordinate,Polygon,Lines) :- aggregate(bag(Line),    in_y_range_at_poly(Coordinate,Line,Polygon), Lines).

traverses_ray(X:Y, Lines, Count) :- aggregate(bag(Line), is_left_half_plane(X:Y, Line, Lines, <), IntersectingLines), length(IntersectingLines, Count).

% This is the entry point predicate
inside_poly(X:Y,Polygon,Answer) :- all_in_range(Y,Polygon,Lines), traverses_ray(X:Y, Lines, Count), (1 is mod(Count,2)->Answer=inside;Answer=outside).

Answer 17

I've made a Python implementation of nirg's c++ code:

Inputs

• bounding_points: nodes that make up the polygon.

• bounding_box_positions: candidate points to filter. (In my implementation created from the bounding box.

  (The inputs are lists of tuples in the format: [(xcord, ycord), ...])

Returns

• All the points that are inside the polygon.

def polygon_ray_casting(self, bounding_points, bounding_box_positions):
    # Arrays containing the x- and y-coordinates of the polygon's vertices.
    vertx = [point[0] for point in bounding_points]
    verty = [point[1] for point in bounding_points]
    # Number of vertices in the polygon
    nvert = len(bounding_points)
    # Points that are inside
    points_inside = []

    # For every candidate position within the bounding box
    for idx, pos in enumerate(bounding_box_positions):
        testx, testy = (pos[0], pos[1])
        c = 0
        for i in range(0, nvert):
            j = i - 1 if i != 0 else nvert - 1
            if( ((verty[i] > testy ) != (verty[j] > testy))   and
                    (testx < (vertx[j] - vertx[i]) * (testy - verty[i]) / (verty[j] - verty[i]) + vertx[i]) ):
                c += 1
        # If odd, that means that we are inside the polygon
        if c % 2 == 1: 
            points_inside.append(pos)


    return points_inside

Again, the idea is taken from here

Answer 18

I realize this is old, but here is a ray casting algorithm implemented in Cocoa, in case anyone is interested. Not sure it is the most efficient way to do things, but it may help someone out.

- (BOOL)shape:(NSBezierPath *)path containsPoint:(NSPoint)point
{
    NSBezierPath *currentPath = [path bezierPathByFlatteningPath];
    BOOL result;
    float aggregateX = 0; //I use these to calculate the centroid of the shape
    float aggregateY = 0;
    NSPoint firstPoint[1];
    [currentPath elementAtIndex:0 associatedPoints:firstPoint];
    float olderX = firstPoint[0].x;
    float olderY = firstPoint[0].y;
    NSPoint interPoint;
    int noOfIntersections = 0;

    for (int n = 0; n < [currentPath elementCount]; n++) {
        NSPoint points[1];
        [currentPath elementAtIndex:n associatedPoints:points];
        aggregateX += points[0].x;
        aggregateY += points[0].y;
    }

    for (int n = 0; n < [currentPath elementCount]; n++) {
        NSPoint points[1];

        [currentPath elementAtIndex:n associatedPoints:points];
        //line equations in Ax + By = C form
        float _A_FOO = (aggregateY/[currentPath elementCount]) - point.y;  
        float _B_FOO = point.x - (aggregateX/[currentPath elementCount]);
        float _C_FOO = (_A_FOO * point.x) + (_B_FOO * point.y);

        float _A_BAR = olderY - points[0].y;
        float _B_BAR = points[0].x - olderX;
        float _C_BAR = (_A_BAR * olderX) + (_B_BAR * olderY);

        float det = (_A_FOO * _B_BAR) - (_A_BAR * _B_FOO);
        if (det != 0) {
            //intersection points with the edges
            float xIntersectionPoint = ((_B_BAR * _C_FOO) - (_B_FOO * _C_BAR)) / det;
            float yIntersectionPoint = ((_A_FOO * _C_BAR) - (_A_BAR * _C_FOO)) / det;
            interPoint = NSMakePoint(xIntersectionPoint, yIntersectionPoint);
            if (olderX <= points[0].x) {
                //doesn't matter in which direction the ray goes, so I send it right-ward.
                if ((interPoint.x >= olderX && interPoint.x <= points[0].x) && (interPoint.x > point.x)) {  
                    noOfIntersections++;
                }
            } else {
                if ((interPoint.x >= points[0].x && interPoint.x <= olderX) && (interPoint.x > point.x)) {
                     noOfIntersections++;
                } 
            }
        }
        olderX = points[0].x;
        olderY = points[0].y;
    }
    if (noOfIntersections % 2 == 0) {
        result = FALSE;
    } else {
        result = TRUE;
    }
    return result;
}

Answer 19

C# version of nirg's answer is here: I'll just share the code. It may save someone some time.

public static bool IsPointInPolygon(IList<Point> polygon, Point testPoint) {
            bool result = false;
            int j = polygon.Count() - 1;
            for (int i = 0; i < polygon.Count(); i++) {
                if (polygon[i].Y < testPoint.Y && polygon[j].Y >= testPoint.Y || polygon[j].Y < testPoint.Y && polygon[i].Y >= testPoint.Y) {
                    if (polygon[i].X + (testPoint.Y - polygon[i].Y) / (polygon[j].Y - polygon[i].Y) * (polygon[j].X - polygon[i].X) < testPoint.X) {
                        result = !result;
                    }
                }
                j = i;
            }
            return result;
        }

Answer 20

VBA VERSION:

Note: Remember that if your polygon is an area within a map that Latitude/Longitude are Y/X values as opposed to X/Y (Latitude = Y, Longitude = X) due to from what I understand are historical implications from way back when Longitude was not a measurement.

CLASS MODULE: CPoint

Private pXValue As Double
Private pYValue As Double

'''''X Value Property'''''

Public Property Get X() As Double
    X = pXValue
End Property

Public Property Let X(Value As Double)
    pXValue = Value
End Property

'''''Y Value Property'''''

Public Property Get Y() As Double
    Y = pYValue
End Property

Public Property Let Y(Value As Double)
    pYValue = Value
End Property

MODULE:

Public Function isPointInPolygon(p As CPoint, polygon() As CPoint) As Boolean

    Dim i As Integer
    Dim j As Integer
    Dim q As Object
    Dim minX As Double
    Dim maxX As Double
    Dim minY As Double
    Dim maxY As Double
    minX = polygon(0).X
    maxX = polygon(0).X
    minY = polygon(0).Y
    maxY = polygon(0).Y

    For i = 1 To UBound(polygon)
        Set q = polygon(i)
        minX = vbMin(q.X, minX)
        maxX = vbMax(q.X, maxX)
        minY = vbMin(q.Y, minY)
        maxY = vbMax(q.Y, maxY)
    Next i

    If p.X < minX Or p.X > maxX Or p.Y < minY Or p.Y > maxY Then
        isPointInPolygon = False
        Exit Function
    End If


    ' SOURCE: http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html

    isPointInPolygon = False
    i = 0
    j = UBound(polygon)

    Do While i < UBound(polygon) + 1
        If (polygon(i).Y > p.Y) Then
            If (polygon(j).Y < p.Y) Then
                If p.X < (polygon(j).X - polygon(i).X) * (p.Y - polygon(i).Y) / (polygon(j).Y - polygon(i).Y) + polygon(i).X Then
                    isPointInPolygon = True
                    Exit Function
                End If
            End If
        ElseIf (polygon(i).Y < p.Y) Then
            If (polygon(j).Y > p.Y) Then
                If p.X < (polygon(j).X - polygon(i).X) * (p.Y - polygon(i).Y) / (polygon(j).Y - polygon(i).Y) + polygon(i).X Then
                    isPointInPolygon = True
                    Exit Function
                End If
            End If
        End If
        j = i
        i = i + 1
    Loop   
End Function

Function vbMax(n1, n2) As Double
    vbMax = IIf(n1 > n2, n1, n2)
End Function

Function vbMin(n1, n2) As Double
    vbMin = IIf(n1 > n2, n2, n1)
End Function


Sub TestPointInPolygon()

    Dim i As Integer
    Dim InPolygon As Boolean

'   MARKER Object
    Dim p As CPoint
    Set p = New CPoint
    p.X = <ENTER X VALUE HERE>
    p.Y = <ENTER Y VALUE HERE>

'   POLYGON OBJECT
    Dim polygon() As CPoint
    ReDim polygon(<ENTER VALUE HERE>) 'Amount of vertices in polygon - 1
    For i = 0 To <ENTER VALUE HERE> 'Same value as above
       Set polygon(i) = New CPoint
       polygon(i).X = <ASSIGN X VALUE HERE> 'Source a list of values that can be looped through
       polgyon(i).Y = <ASSIGN Y VALUE HERE> 'Source a list of values that can be looped through
    Next i

    InPolygon = isPointInPolygon(p, polygon)
    MsgBox InPolygon

End Sub

Answer 21

Surprised nobody brought this up earlier, but for the pragmatists requiring a database: MongoDB has excellent support for Geo queries including this one.

What you are looking for is:

db.neighborhoods.findOne({ geometry: { $geoIntersects: { $geometry: { type: "Point", coordinates: [ "longitude", "latitude" ] } } } })

Neighborhoods is the collection that stores one or more polygons in standard GeoJson format. If the query returns null it is not intersected otherwise it is.

Very well documented here: https://docs.mongodb.com/manual/tutorial/geospatial-tutorial/

The performance for more than 6,000 points classified in a 330 irregular polygon grid was less than one minute with no optimization at all and including the time to update documents with their respective polygon.

Answer 22

.Net port:

    static void Main(string[] args)
    {

        Console.Write("Hola");
        List<double> vertx = new List<double>();
        List<double> verty = new List<double>();

        int i, j, c = 0;

        vertx.Add(1);
        vertx.Add(2);
        vertx.Add(1);
        vertx.Add(4);
        vertx.Add(4);
        vertx.Add(1);

        verty.Add(1);
        verty.Add(2);
        verty.Add(4);
        verty.Add(4);
        verty.Add(1);
        verty.Add(1);

        int nvert = 6;  //Vértices del poligono

        double testx = 2;
        double testy = 5;


        for (i = 0, j = nvert - 1; i < nvert; j = i++)
        {
            if (((verty[i] > testy) != (verty[j] > testy)) &&
             (testx < (vertx[j] - vertx[i]) * (testy - verty[i]) / (verty[j] - verty[i]) + vertx[i]))
                c = 1;
        }
    }

Answer 23

Heres a point in polygon test in C that isn't using ray-casting. And it can work for overlapping areas (self intersections), see the use_holes argument.

/* math lib (defined below) */
static float dot_v2v2(const float a[2], const float b[2]);
static float angle_signed_v2v2(const float v1[2], const float v2[2]);
static void copy_v2_v2(float r[2], const float a[2]);

/* intersection function */
bool isect_point_poly_v2(const float pt[2], const float verts[][2], const unsigned int nr,
                         const bool use_holes)
{
    /* we do the angle rule, define that all added angles should be about zero or (2 * PI) */
    float angletot = 0.0;
    float fp1[2], fp2[2];
    unsigned int i;
    const float *p1, *p2;

    p1 = verts[nr - 1];

    /* first vector */
    fp1[0] = p1[0] - pt[0];
    fp1[1] = p1[1] - pt[1];

    for (i = 0; i < nr; i++) {
        p2 = verts[i];

        /* second vector */
        fp2[0] = p2[0] - pt[0];
        fp2[1] = p2[1] - pt[1];

        /* dot and angle and cross */
        angletot += angle_signed_v2v2(fp1, fp2);

        /* circulate */
        copy_v2_v2(fp1, fp2);
        p1 = p2;
    }

    angletot = fabsf(angletot);
    if (use_holes) {
        const float nested = floorf((angletot / (float)(M_PI * 2.0)) + 0.00001f);
        angletot -= nested * (float)(M_PI * 2.0);
        return (angletot > 4.0f) != ((int)nested % 2);
    }
    else {
        return (angletot > 4.0f);
    }
}

/* math lib */

static float dot_v2v2(const float a[2], const float b[2])
{
    return a[0] * b[0] + a[1] * b[1];
}

static float angle_signed_v2v2(const float v1[2], const float v2[2])
{
    const float perp_dot = (v1[1] * v2[0]) - (v1[0] * v2[1]);
    return atan2f(perp_dot, dot_v2v2(v1, v2));
}

static void copy_v2_v2(float r[2], const float a[2])
{
    r[0] = a[0];
    r[1] = a[1];
}

Note: this is one of the less optimal methods since it includes a lot of calls to atan2f, but it may be of interest to developers reading this thread (in my tests its ~23x slower then using the line intersection method).

Answer 24

If you're using Google Map SDK and want to check if a point is inside a polygon, you can try to use GMSGeometryContainsLocation. It works great!! Here is how that works,

if GMSGeometryContainsLocation(point, polygon, true) {
    print("Inside this polygon.")
} else {
    print("outside this polygon")
}

Here is the reference: https://developers.google.com/maps/documentation/ios-sdk/reference/group___geometry_utils#gaba958d3776d49213404af249419d0ffd

Answer 25

This is a presumably slightly less optimized version of the C code from here which was sourced from this page.

My C++ version uses a std::vector<std::pair<double, double>> and two doubles as an x and y. The logic should be exactly the same as the original C code, but I find mine easier to read. I can't speak for the performance.

bool point_in_poly(std::vector<std::pair<double, double>>& verts, double point_x, double point_y)
{
    bool in_poly = false;
    auto num_verts = verts.size();
    for (int i = 0, j = num_verts - 1; i < num_verts; j = i++) {
        double x1 = verts[i].first;
        double y1 = verts[i].second;
        double x2 = verts[j].first;
        double y2 = verts[j].second;

        if (((y1 > point_y) != (y2 > point_y)) &&
            (point_x < (x2 - x1) * (point_y - y1) / (y2 - y1) + x1))
            in_poly = !in_poly;
    }
    return in_poly;
}

The original C code is

int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy)
{
  int i, j, c = 0;
  for (i = 0, j = nvert-1; i < nvert; j = i++) {
    if ( ((verty[i]>testy) != (verty[j]>testy)) &&
     (testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )
       c = !c;
  }
  return c;
}

Answer 26

Yet another numpyic implementation which I believe is the most concise one out of all the answers so far.

For example, let's say we have a polygon with polygon hollows that looks like this:

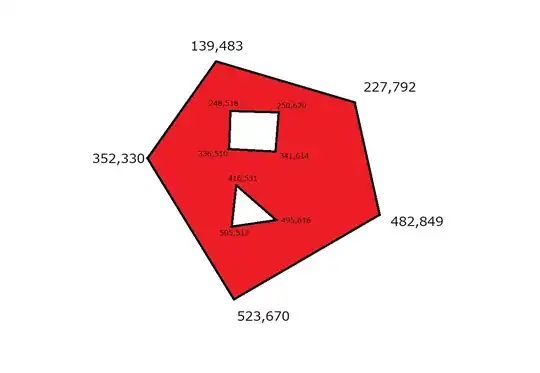
The 2D coordinates for the vertices of the large polygon are

[[139, 483], [227, 792], [482, 849], [523, 670], [352, 330]]

The coordinates for the vertices of the square hollow are

[[248, 518], [336, 510], [341, 614], [250, 620]]

The coordinates for the vertices of the triangle hollow are

[[416, 531], [505, 517], [495, 616]]

Say we want to test two points [296, 557] and [422, 730] if they are within the red area (excluding the edges). If we locate the two points, it will look like this:

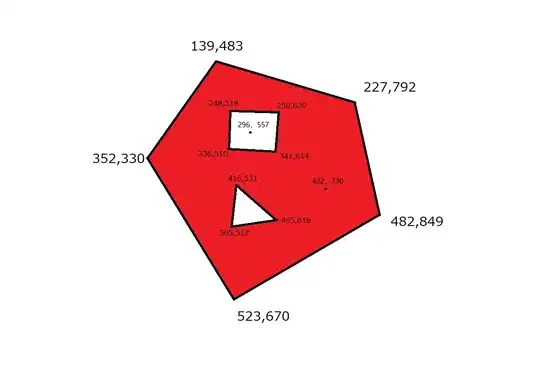
Obviously, [296, 557] is not inside the read area, whereas [422, 730] is.

My solution is based on the winding number algorithm. Below is my 4-line python code using only numpy:

def detect(points, *polygons):
    import numpy as np
    endpoint1 = np.r_[tuple(np.roll(p, 1, 0) for p in polygons)][:, None] - points
    endpoint2 = np.r_[polygons][:, None] - points
    p1, p2 = np.cross(endpoint1, endpoint2), np.einsum('...i,...i', endpoint1, endpoint2)
    return ~((p1.sum(0) < 0) ^ (abs(np.arctan2(p1, p2).sum(0)) > np.pi) | ((p1 == 0) & (p2 <= 0)).any(0))

To test the implementation:

points = [[296, 557], [422, 730]]
polygon1 = [[139, 483], [227, 792], [482, 849], [523, 670], [352, 330]]
polygon2 = [[248, 518], [336, 510], [341, 614], [250, 620]]
polygon3 = [[416, 531], [505, 517], [495, 616]]

print(detect(points, polygon1, polygon2, polygon3))

Output:

[False  True]

Answer 27

For Detecting hit on Polygon we need to test two things:

1. If Point is inside polygon area. (can be accomplished by Ray-Casting Algorithm)
2. If Point is on the polygon border(can be accomplished by same algorithm which is used for point detection on polyline(line)).

Answer 28

To deal with the following special cases in Ray casting algorithm:

1. The ray overlaps one of the polygon's side.
2. The point is inside of the polygon and the ray passes through a vertex of the polygon.
3. The point is outside of the polygon and the ray just touches one of the polygon's angle.

Check Determining Whether A Point Is Inside A Complex Polygon. The article provides an easy way to resolve them so there will be no special treatment required for the above cases.

Answer 29

You can do this by checking if the area formed by connecting the desired point to the vertices of your polygon matches the area of the polygon itself.

Or you could check if the sum of the inner angles from your point to each pair of two consecutive polygon vertices to your check point sums to 360, but I have the feeling that the first option is quicker because it doesn't involve divisions nor calculations of inverse of trigonometric functions.

I don't know what happens if your polygon has a hole inside it but it seems to me that the main idea can be adapted to this situation

You can as well post the question in a math community. I bet they have one million ways of doing that

Answer 30

If you are looking for a java-script library there's a javascript google maps v3 extension for the Polygon class to detect whether a point resides within it.

var polygon = new google.maps.Polygon([], "#000000", 1, 1, "#336699", 0.3);
var isWithinPolygon = polygon.containsLatLng(40, -90);

Google Extension Github

Answer 31

When using qt (Qt 4.3+), one can use QPolygon's function containsPoint

Answer 32

The answer depends on if you have the simple or complex polygons. Simple polygons must not have any line segment intersections. So they can have the holes but lines can't cross each other. Complex regions can have the line intersections - so they can have the overlapping regions, or regions that touch each other just by a single point.

For simple polygons the best algorithm is Ray casting (Crossing number) algorithm. For complex polygons, this algorithm doesn't detect points that are inside the overlapping regions. So for complex polygons you have to use Winding number algorithm.

Here is an excellent article with C implementation of both algorithms. I tried them and they work well.

http://geomalgorithms.com/a03-_inclusion.html

Answer 33

Scala version of solution by nirg (assumes bounding rectangle pre-check is done separately):

def inside(p: Point, polygon: Array[Point], bounds: Bounds): Boolean = {

  val length = polygon.length

  @tailrec
  def oddIntersections(i: Int, j: Int, tracker: Boolean): Boolean = {
    if (i == length)
      tracker
    else {
      val intersects = (polygon(i).y > p.y) != (polygon(j).y > p.y) && p.x < (polygon(j).x - polygon(i).x) * (p.y - polygon(i).y) / (polygon(j).y - polygon(i).y) + polygon(i).x
      oddIntersections(i + 1, i, if (intersects) !tracker else tracker)
    }
  }

  oddIntersections(0, length - 1, tracker = false)
}

Answer 34

Here is golang version of @nirg answer (inspired by C# code by @@m-katz)

func isPointInPolygon(polygon []point, testp point) bool {
    minX := polygon[0].X
    maxX := polygon[0].X
    minY := polygon[0].Y
    maxY := polygon[0].Y

    for _, p := range polygon {
        minX = min(p.X, minX)
        maxX = max(p.X, maxX)
        minY = min(p.Y, minY)
        maxY = max(p.Y, maxY)
    }

    if testp.X < minX || testp.X > maxX || testp.Y < minY || testp.Y > maxY {
        return false
    }

    inside := false
    j := len(polygon) - 1
    for i := 0; i < len(polygon); i++ {
        if (polygon[i].Y > testp.Y) != (polygon[j].Y > testp.Y) && testp.X < (polygon[j].X-polygon[i].X)*(testp.Y-polygon[i].Y)/(polygon[j].Y-polygon[i].Y)+polygon[i].X {
            inside = !inside
        }
        j = i
    }

    return inside
}

Answer 35

This seems to work in R (apologies for ugliness, would like to see better version!).

pnpoly <- function(nvert,vertx,verty,testx,testy){
          c <- FALSE
          j <- nvert 
          for (i in 1:nvert){
              if( ((verty[i]>testy) != (verty[j]>testy)) && 
   (testx < (vertx[j]-vertx[i])*(testy-verty[i])/(verty[j]-verty[i])+vertx[i]))
            {c <- !c}
             j <- i}
   return(c)}

Answer 36

For the completeness, here's the lua implementation of the algorithm provided by nirg and discussed by Mecki:

function pnpoly(area, test)
    local inside = false
    local tx, ty = table.unpack(test)
    local j = #area
    for i=1, #area do
        local vxi, vyi = table.unpack(area[i])
        local vxj, vyj = table.unpack(area[j])
        if (vyi > ty) ~= (vyj > ty)
        and tx < (vxj - vxi)*(ty - vyi)/(vyj - vyi) + vxi
        then
            inside = not inside
        end
        j = i
    end
    return inside
end

The variable area is a table of points which are in turn stored as 2D tables. Example:

> A = {{2, 1}, {1, 2}, {15, 3}, {3, 4}, {5, 3}, {4, 1.5}}
> T = {2, 1.1}
> pnpoly(A, T)
true

The link to GitHub Gist.

Answer 37

from typing import Iterable

def pnpoly(verts, x, y):
    #check if x and/or y is iterable
    xit, yit = isinstance(x, Iterable), isinstance(y, Iterable)
    #if not iterable, make an iterable of length 1
    X = x if xit else (x, )
    Y = y if yit else (y, )
    #store verts length as a range to juggle j
    r = range(len(verts))
    #final results if x or y is iterable
    results = []
    #traverse x and y coordinates
    for xp in X:
        for yp in Y:
            c = 0 #reset c at every new position
            for i in r:
                j = r[i-1] #set j to position before i
                #store a few arguments to shorten the if statement
                yneq       = (verts[i][1] > yp) != (verts[j][1] > yp)
                xofs, yofs = (verts[j][0] - verts[i][0]), (verts[j][1] - verts[i][1])
                #if we have crossed a line, increment c
                if (yneq and (xp < xofs * (yp - verts[i][1]) / yofs + verts[i][0])):
                    c += 1
            #if c is odd store the coordinates        
            if c%2:
                results.append((xp, yp))
    #return either coordinates or a bool, depending if x or y was an iterable
    return results if (xit or yit) else bool(c%2)

This python version is versatile. You can either input a single x and single y value for a True/False result or you can use range for x and y to traverse an entire grid of points. If ranges are used a list of x/y pairs for all True points is returned. The vertices argument expects a 2-dimensional Iterable of x/y pairs, such as: [(x1,y1), (x2,y2), ...]

example usage:

vertices = [(25,25), (75,25), (75,75), (25,75)]
pnpoly(vertices, 50, 50) #True
pnpoly(vertices, range(100), range(100)) #[(25,25), (25,26), (25,27), ...]

Actually, even these would work.

pnpoly(vertices, 50, range(100)) #check 0 to 99 y at x of 50
pnpoly(vertices, range(100), 50) #check 0 to 99 x at y of 50

Answer 38

Like David Segonds' answer suggests I use an approach of angle summation derived from my concave polygon drawing algorithm. It relies of adding up the approximate angles of subtriangles around the point to obtain a weight. A weight around 1.0 means the point is inside the triangle, a weight around 0.0 means outside, a weight around -1.0 is what happens when inside the polygon but in reverse order (like with one of the halves of a bowtie-shaped tetragon) and a weight of NAN if exactly on an edge. The reason it's not slow is that angles don't need to be estimated accurately at all. Holes can be handled by treating them as separate polygons and subtracting the weights.

typedef struct { double x, y; } xy_t;

xy_t sub_xy(xy_t a, xy_t b)
{
    a.x -= b.x;
    a.y -= b.y;
    return a;
}

double calc_sharp_subtriangle_pixel_weight(xy_t p0, xy_t p1)
{
    xy_t rot, r0, r1;
    double weight;

    // Rotate points (unnormalised)
    rot = sub_xy(p1, p0);
    r0.x = rot.x*p0.y - rot.y*p0.x;
    r0.y = rot.x*p0.x + rot.y*p0.y;
    r1.y = rot.x*p1.x + rot.y*p1.y;

    // Calc weight
    weight = subtriangle_angle_approx(r1.y, r0.x) - subtriangle_angle_approx(r0.y, r0.x);

    return weight;
}

double calc_sharp_polygon_pixel_weight(xy_t p, xy_t *corner, int corner_count)
{
    int i;
    xy_t p0, p1;
    double weight = 0.;

    p0 = sub_xy(corner[corner_count-1], p);
    for (i=0; i < corner_count; i++)
    {
        // Transform corner coordinates
        p1 = sub_xy(corner[i], p);

        // Calculate weight for each subtriangle
        weight += calc_sharp_subtriangle_pixel_weight(p0, p1);
        p0 = p1;
    }

    return weight;
}

So for each segment of the polygon a subtriangle is formed with the point being evaluated, then each subtriangle is rotated to have its approximate angles evaluated and add to a weight.

Calls to subtriangle_angle_approx(y, x) can be replaced with atan2(y, x) / (2.*pi), however a very rough approximation will be precise enough:

double subtriangle_angle_approx(double y, double x)
{
    double angle, d;
    int obtuse;

    if (x == 0.)
        return NAN;

    obtuse = fabs(y) > fabs(x);
    if (obtuse)
        swap_double(&y, &x);

    // Core of the approximation, a very loosely approximate atan(y/x) / (2.*pi) over ]-1 , 1[
    d = y / x;
    angle = 0.13185 * d;

    if (obtuse)
        angle = sign(d)*0.25 - angle;

    return angle;
}

Answer 39

Here is Rust version of @nirg answer(Philipp Lenssen javascript version) I give this answser because i get many help form this site,and i translate javascript version to rust for a exceise and hope can help some one,the last reason is that in my work i will translate this code as a wasm to improve performance of my canvas,this is as a start.my poor english aaa...,forgive me `

pub struct Point {
    x: f32,
    y: f32,
}
pub fn point_is_in_poly(pt: Point, polygon: &Vec<Point>) -> bool {
    let mut is_inside = false;

    let max_x = polygon.iter().map(|pt| pt.x).reduce(f32::max).unwrap();
    let min_x = polygon.iter().map(|pt| pt.x).reduce(f32::min).unwrap();
    let max_y = polygon.iter().map(|pt| pt.y).reduce(f32::max).unwrap();
    let min_y = polygon.iter().map(|pt| pt.y).reduce(f32::min).unwrap();

    if pt.x < min_x || pt.x > max_x || pt.y < min_y || pt.y > max_y {
        return is_inside;
    }

    let len = polygon.len();
    let mut j = len - 1;

    for i in 0..len {
        let y_i_value = polygon[i].y > pt.y;
        let y_j_value = polygon[j].y > pt.y;
        let last_check = (polygon[j].x - polygon[i].x) * (pt.y - polygon[i].y)
            / (polygon[j].y - polygon[i].y)
            + polygon[i].x;
        if y_i_value != y_j_value && pt.x < last_check {
            is_inside = !is_inside;
        }
        j = i;
    }
    is_inside
}


let pt = Point {
    x: 1266.753,
    y: 97.655,
};
let polygon = vec![
    Point {
        x: 725.278,
        y: 203.586,
    },
    Point {
        x: 486.831,
        y: 441.931,
    },
    Point {
        x: 905.77,
        y: 445.241,
    },
    Point {
        x: 1026.649,
        y: 201.931,
    },
];
let pt1 = Point {
    x: 725.278,
    y: 203.586,
};
let pt2 = Point {
    x: 872.652,
    y: 321.103,
};
println!("{}", point_is_in_poly(pt, &polygon));// false
println!("{}", point_is_in_poly(pt1, &polygon)); // true
println!("{}", point_is_in_poly(pt2, &polygon));// true

`

Answer 40

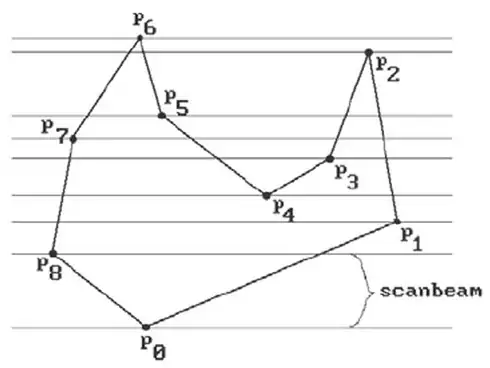
Here's an algorithm faster than everybody else's algorithm for most cases.

It's new and elegant. We spend O(n * log(n)) time building a table that will allow us to test point-in-polygon in O(log(n) + k) time.

Rather than ray-tracing or angles, you can get significantly faster results for multiple checks of the same polygon using a scanbeam table. We have to prebuild a scanbeam active edge table which is what most of the code is doing.

We calculate the scanbeam and the active edges for that position in the y-direction. We make a list of points sorted by their y-component and we iterate through this list, for two events. Start-Y and End-Y, we track the active edges as we process the list. We process the events in order and for each scanbeam we record the y-value of the event and the active edges at each event (events being start-y and end-y) but we only record these when our event-y is different than last time (so everything at the event point is processed before we mark it in our table).

So we get our table:

1. []
2. p6p5, p6p7
3. p6p5, p6p7, p2p3, p2p1
4. p6p7, p5p4, p2p3, p3p1
5. p7p8, p5p4, p2p3, p2p1
6. p7p8, p5p4, p3p4, p2p1
7. p7p8, p2p1
8. p7p8, p1p0
9. p8p0, p1p0
10. []

The actual code doing the work is just a couple lines after this table is built.

• Note: the code here is using complex values as points. So .real is .x and .imag is .y.

def point_in_scantable(actives_table, events, xi, point):
    beam = bisect(events, point.imag) - 1  # Binary search in sorted array.
    actives_at_y = actives_table[beam]
    total = sum([point.real > xi(e, point.imag) for e in actives_at_y])
    return bool(total % 2)

We binary search into the events to find the actives_at_y for the specific value. For all the actives at that y we calculate the segments x value at the specific y of our point. We add 1 each time this x-intercept is bigger than our point's x-component. We then mod that total by 2. (This is the even-odd fill rule, you can easily adapt this to any other fill rule).

Complete Code:

from bisect import bisect

def build_edge_list(polygon):
    edge_list = []
    for i in range(1, len(polygon)):
        if (polygon[i].imag, polygon[i].real) < (polygon[i - 1].imag, polygon[i - 1].real):
            edge_list.append((polygon[i], i))
            edge_list.append((polygon[i - 1], ~i))
        else:
            edge_list.append((polygon[i], ~i))
            edge_list.append((polygon[i - 1], i))

    def sort_key(e):
        return e[0].imag, e[0].real, ~e[1]

    edge_list.sort(key=sort_key)
    return edge_list


def build_scanbeam(edge_list):
    actives_table = []
    events = []
    y = -float("inf")
    actives = []
    for pt, index in edge_list:
        if y != pt.imag:
            actives_table.append(list(actives))
            events.append(y)
        if index >= 0:
            actives.append(index)
        else:
            actives.remove(~index)
        y = pt.imag
    return actives_table, events

def point_in_polygon(polygon, point):
    def x_intercept(e, y):
        pt0 = polygon[e-1]
        pt1 = polygon[e]
        if pt1.real - pt0.real == 0:
            return pt0.real
        m = (pt1.imag - pt0.imag) / (pt1.real - pt0.real)
        b = pt0.imag - (m * pt0.real)
        return (y - b) / m

    edge_list = build_edge_list(polygon)
    actives_table, events = build_scanbeam(edge_list)
    try:
        if len(point):
            return [point_in_scantable(actives_table, events, x_intercept, p) for p in point]
    except TypeError:
        return point_in_scantable(actives_table, events, x_intercept, point)

def point_in_scantable(actives_table, events, xi, point):
    beam = bisect(events, point.imag) - 1  # Binary search in sorted array.
    actives_at_y = actives_table[beam]
    total = sum([point.real > xi(e, point.imag) for e in actives_at_y])
    return bool(total % 2)

If we ignore then O(n*log(n)) buildtime for the scantable. We're actually looking things up in O(log(n) + k) time. Where n is the size of the number of segments in the polygon and k is the typical number of active edges in said polygon. The other methods for raytracing actually needs O(n) time. Each time we check a point it iterates the entire polygon. So even with this notably suboptimal implementation of this, it beats all the rest of them hands down.

---

There's a few performance tricks that could be done, for example, we can lower the time complexity to O(log(n) + log(k)) time. To do this we would implement Bentley-Ottmann into the sweep line, and rather than processing the intersections as different events, we split the lines at the intersections. We then also sort the active edges by their x-intercepts. We then know that no intersections occur during a scanbeam and since we sorted our segments (taking care to order them correctly within the scanbeam even if they start at the same initial point (you need to look at the slopes, or just compare midpoints of the segments). We then have a sorted intersection-less actives lists scanbeam table which means we can binary search into active edge list as well. Though that sounds like a lot of work for a value of k which is going to be typically 2 or maybe 4.

Also, since this basically becomes a lookup table and some minimal calculations for x-intercept it's much more able to be done with a GPU. You don't need to loop over the polygon anymore. So you can actually mass calculate these points with things like numpy where you get performance boosts for doing all the calculations at once.

Answer 41

Barycentric coordinates can be used to describe the position of a point within a triangle. They represent the ratios of the distances between the point and the vertices of the triangle.

In a triangle with vertices A, B, and C, any point P within the triangle can be expressed using barycentric coordinates (u, v, w), where u, v, and w represent the ratios of the distances between P and the vertices A, B, and C, respectively. The coordinates must satisfy the condition u + v + w = 1.

It's worth noting that the barycentric coordinates applies to any polygon, regardless of its shape.

For a concave polygon, the barycentric coordinates of a point within the polygon are still determined by the ratios of the distances between the point and the vertices. The only difference is that some of the barycentric coordinates may be negative, indicating that the point lies outside the polygon. In such cases, the sum of the coordinates will not equal 1.

Similarly, for a convex polygon, the barycentric coordinates of a point within the polygon will always be non-negative and sum up to 1.

Whether the shape is concave or convex does not affect the calculation of the barycentric coordinates. The key is to ensure that the coordinates are correctly computed based on the relative distances between the point and the vertices of the polygon.

Below you can see a matlab implementation for four vertex shape.

function isInside = isPointInsideQuadrilateral(x, y, x1, y1, x2, y2, x3, y3, x4, y4)
    % Calculate barycentric coordinates
    denominator1 = (y2 - y1)*(x4 - x1) + (x1 - x2)*(y4 - y1);
    alpha1 = ((y2 - y1)*(x - x1) + (x1 - x2)*(y - y1)) / denominator1;
    beta1 = ((y1 - y4)*(x - x1) + (x4 - x1)*(y - y1)) / denominator1;
    gamma1 = 1 - alpha1 - beta1;

    denominator2 = (y3 - y2)*(x4 - x2) + (x2 - x3)*(y4 - y2);
    alpha2 = ((y3 - y2)*(x - x2) + (x2 - x3)*(y - y2)) / denominator2;
    beta2 = ((y2 - y4)*(x - x2) + (x4 - x2)*(y - y2)) / denominator2;
    gamma2 = 1 - alpha2 - beta2;

    isInside = (alpha1 >= 0 && beta1 >= 0 && gamma1 >= 0) || (alpha2 >= 0 && beta2 >= 0 && gamma2 >= 0);
end

This technique is quite fast and has high precision.

Answer 42

This only works for convex shapes, but Minkowski Portal Refinement, and GJK are also great options for testing if a point is in a polygon. You use minkowski subtraction to subtract the point from the polygon, then run those algorithms to see if the polygon contains the origin.

Also, interestingly, you can describe your shapes a bit more implicitly using support functions which take a direction vector as input and spit out the farthest point along that vector. This allows you to describe any convex shape.. curved, made out of polygons, or mixed. You can also do operations to combine the results of simple support functions to make more complex shapes.

More info: http://xenocollide.snethen.com/mpr2d.html

Also, game programming gems 7 talks about how to do this in 3d (: