Detect and exclude outliers in a pandas DataFrame

Question

I have a pandas data frame with few columns.

Now I know that certain rows are outliers based on a certain column value.

For instance

column 'Vol' has all values around 12xx and one value is 4000 (outlier).

Now I would like to exclude those rows that have Vol column like this.

So, essentially I need to put a filter on the data frame such that we select all rows where the values of a certain column are within, say, 3 standard deviations from mean.

What is an elegant way to achieve this?

Answer 1

Remove all rows that have outliers in, at least, one column

If you have multiple columns in your dataframe and would like to remove all rows that have outliers in at least one column, the following expression would do that in one shot:

import pandas as pd
import numpy as np
from scipy import stats


df = pd.DataFrame(np.random.randn(100, 3))

df[(np.abs(stats.zscore(df)) < 3).all(axis=1)]

Description:

• For each column, it first computes the Z-score of each value in the column, relative to the column mean and standard deviation.
• It then takes the absolute Z-score because the direction does not matter, only if it is below the threshold.
• all(axis=1) ensures that for each row, all column satisfy the constraint.
• Finally, the result of this condition is used to index the dataframe.

Filter other columns based on a single column

• Specify a column for the zscore, df[0] for example, and remove .all(axis=1).

df[(np.abs(stats.zscore(df[0])) < 3)]

Answer 2

For each of your dataframe column, you could get quantile with:

q = df["col"].quantile(0.99)

and then filter with:

df[df["col"] < q]

If one need to remove lower and upper outliers, combine condition with an AND statement:

q_low = df["col"].quantile(0.01)
q_hi  = df["col"].quantile(0.99)

df_filtered = df[(df["col"] < q_hi) & (df["col"] > q_low)]

Answer 3

Use boolean indexing as you would do in numpy.array

df = pd.DataFrame({'Data':np.random.normal(size=200)})
# example dataset of normally distributed data. 

df[np.abs(df.Data-df.Data.mean()) <= (3*df.Data.std())]
# keep only the ones that are within +3 to -3 standard deviations in the column 'Data'.

df[~(np.abs(df.Data-df.Data.mean()) > (3*df.Data.std()))]
# or if you prefer the other way around

For a series it is similar:

S = pd.Series(np.random.normal(size=200))
S[~((S-S.mean()).abs() > 3*S.std())]

Answer 4

This answer is similar to that provided by @tanemaki, but uses a lambda expression instead of scipy stats.

df = pd.DataFrame(np.random.randn(100, 3), columns=list('ABC'))

standard_deviations = 3
df[df.apply(lambda x: np.abs(x - x.mean()) / x.std() < standard_deviations)
   .all(axis=1)]

To filter the DataFrame where only ONE column (e.g. 'B') is within three standard deviations:

df[((df['B'] - df['B'].mean()) / df['B'].std()).abs() < standard_deviations]

See here for how to apply this z-score on a rolling basis: Rolling Z-score applied to pandas dataframe

Answer 5

Before answering the actual question we should ask another one that's very relevant depending on the nature of your data:

What is an outlier?

Imagine the series of values [3, 2, 3, 4, 999] (where the 999 seemingly doesn't fit in) and analyse various ways of outlier detection

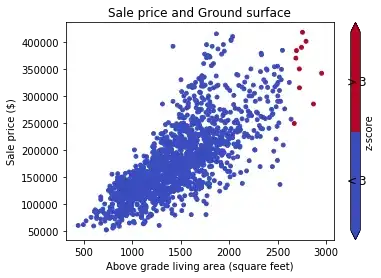
Z-Score

The problem here is that the value in question distorts our measures mean and std heavily, resulting in inconspicious z-scores of roughly [-0.5, -0.5, -0.5, -0.5, 2.0], keeping every value within two standard deviations of the mean. One very large outlier might hence distort your whole assessment of outliers. I would discourage this approach.

Quantile Filter

A way more robust approach is given is this answer, eliminating the bottom and top 1% of data. However, this eliminates a fixed fraction independant of the question if these data are really outliers. You might loose a lot of valid data, and on the other hand still keep some outliers if you have more than 1% or 2% of your data as outliers.

IQR-distance from Median

Even more robust version of the quantile principle: Eliminate all data that is more than f times the interquartile range away from the median of the data. That's also the transformation that sklearn's RobustScaler uses for example. IQR and median are robust to outliers, so you outsmart the problems of the z-score approach.

In a normal distribution, we have roughly iqr=1.35*s, so you would translate z=3 of a z-score filter to f=2.22 of an iqr-filter. This will drop the 999 in the above example.

The basic assumption is that at least the "middle half" of your data is valid and resembles the distribution well, whereas you also mess up if your distribution has wide tails and a narrow q_25% to q_75% interval.

Advanced Statistical Methods

Of course there are fancy mathematical methods like the Peirce criterion, Grubb's test or Dixon's Q-test just to mention a few that are also suitable for non-normally distributed data. None of them are easily implemented and hence not addressed further.

Code

Replacing all outliers for all numerical columns with np.nan on an example data frame. The method is robust against all dtypes that pandas provides and can easily be applied to data frames with mixed types:

import pandas as pd
import numpy as np                                     

# sample data of all dtypes in pandas (column 'a' has an outlier)         # dtype:
df = pd.DataFrame({'a': list(np.random.rand(8)) + [123456, np.nan],       # float64
                   'b': [0,1,2,3,np.nan,5,6,np.nan,8,9],                  # int64
                   'c': [np.nan] + list("qwertzuio"),                     # object
                   'd': [pd.to_datetime(_) for _ in range(10)],           # datetime64[ns]
                   'e': [pd.Timedelta(_) for _ in range(10)],             # timedelta[ns]
                   'f': [True] * 5 + [False] * 5,                         # bool
                   'g': pd.Series(list("abcbabbcaa"), dtype="category")}) # category
cols = df.select_dtypes('number').columns  # limits to a (float), b (int) and e (timedelta)
df_sub = df.loc[:, cols]


# OPTION 1: z-score filter: z-score < 3
lim = np.abs((df_sub - df_sub.mean()) / df_sub.std(ddof=0)) < 3

# OPTION 2: quantile filter: discard 1% upper / lower values
lim = np.logical_and(df_sub < df_sub.quantile(0.99, numeric_only=False),
                     df_sub > df_sub.quantile(0.01, numeric_only=False))

# OPTION 3: iqr filter: within 2.22 IQR (equiv. to z-score < 3)
iqr = df_sub.quantile(0.75, numeric_only=False) - df_sub.quantile(0.25, numeric_only=False)
lim = np.abs((df_sub - df_sub.median()) / iqr) < 2.22


# replace outliers with nan
df.loc[:, cols] = df_sub.where(lim, np.nan)

To drop all rows that contain at least one nan-value:

df.dropna(subset=cols, inplace=True) # drop rows with NaN in numerical columns
# or
df.dropna(inplace=True)  # drop rows with NaN in any column

Using pandas 1.3 functions:

• pandas.DataFrame.select_dtypes()
• pandas.DataFrame.quantile()
• pandas.DataFrame.where()
• pandas.DataFrame.dropna()

Answer 6

#------------------------------------------------------------------------------
# accept a dataframe, remove outliers, return cleaned data in a new dataframe
# see http://www.itl.nist.gov/div898/handbook/prc/section1/prc16.htm
#------------------------------------------------------------------------------
def remove_outlier(df_in, col_name):
    q1 = df_in[col_name].quantile(0.25)
    q3 = df_in[col_name].quantile(0.75)
    iqr = q3-q1 #Interquartile range
    fence_low  = q1-1.5*iqr
    fence_high = q3+1.5*iqr
    df_out = df_in.loc[(df_in[col_name] > fence_low) & (df_in[col_name] < fence_high)]
    return df_out

Answer 7

Since I haven't seen an answer that deal with numerical and non-numerical attributes, here is a complement answer.

You might want to drop the outliers only on numerical attributes (categorical variables can hardly be outliers).

Function definition

I have extended @tanemaki's suggestion to handle data when non-numeric attributes are also present:

from scipy import stats

def drop_numerical_outliers(df, z_thresh=3):
    # Constrains will contain `True` or `False` depending on if it is a value below the threshold.
    constrains = df.select_dtypes(include=[np.number]) \
        .apply(lambda x: np.abs(stats.zscore(x)) < z_thresh, reduce=False) \
        .all(axis=1)
    # Drop (inplace) values set to be rejected
    df.drop(df.index[~constrains], inplace=True)

Usage

drop_numerical_outliers(df)

Example

Imagine a dataset df with some values about houses: alley, land contour, sale price, ... E.g: Data Documentation

First, you want to visualise the data on a scatter graph (with z-score Thresh=3):

# Plot data before dropping those greater than z-score 3. 
# The scatterAreaVsPrice function's definition has been removed for readability's sake.
scatterAreaVsPrice(df)

# Drop the outliers on every attributes
drop_numerical_outliers(train_df)

# Plot the result. All outliers were dropped. Note that the red points are not
# the same outliers from the first plot, but the new computed outliers based on the new data-frame.
scatterAreaVsPrice(train_df)

Answer 8

For each series in the dataframe, you could use between and quantile to remove outliers.

x = pd.Series(np.random.normal(size=200)) # with outliers
x = x[x.between(x.quantile(.25), x.quantile(.75))] # without outliers

Answer 9

scipy.stats has methods trim1() and trimboth() to cut the outliers out in a single row, according to the ranking and an introduced percentage of removed values.

Answer 10

If you like method chaining, you can get your boolean condition for all numeric columns like this:

df.sub(df.mean()).div(df.std()).abs().lt(3)

Each value of each column will be converted to True/False based on whether its less than three standard deviations away from the mean or not.

Answer 11

Another option is to transform your data so that the effect of outliers is mitigated. You can do this by winsorizing your data.

import pandas as pd
from scipy.stats import mstats
%matplotlib inline

test_data = pd.Series(range(30))
test_data.plot()

# Truncate values to the 5th and 95th percentiles
transformed_test_data = pd.Series(mstats.winsorize(test_data, limits=[0.05, 0.05])) 
transformed_test_data.plot()

Answer 12

You can use boolean mask:

import pandas as pd

def remove_outliers(df, q=0.05):
    upper = df.quantile(1-q)
    lower = df.quantile(q)
    mask = (df < upper) & (df > lower)
    return mask

t = pd.DataFrame({'train': [1,1,2,3,4,5,6,7,8,9,9],
                  'y': [1,0,0,1,1,0,0,1,1,1,0]})

mask = remove_outliers(t['train'], 0.1)

print(t[mask])

output:

   train  y
2      2  0
3      3  1
4      4  1
5      5  0
6      6  0
7      7  1
8      8  1

Answer 13

Since I am in a very early stage of my data science journey, I am treating outliers with the code below.

#Outlier Treatment

def outlier_detect(df):
    for i in df.describe().columns:
        Q1=df.describe().at['25%',i]
        Q3=df.describe().at['75%',i]
        IQR=Q3 - Q1
        LTV=Q1 - 1.5 * IQR
        UTV=Q3 + 1.5 * IQR
        x=np.array(df[i])
        p=[]
        for j in x:
            if j < LTV or j>UTV:
                p.append(df[i].median())
            else:
                p.append(j)
        df[i]=p
    return df

Answer 14

Get the 98th and 2nd percentile as the limits of our outliers

upper_limit = np.percentile(X_train.logerror.values, 98) 
lower_limit = np.percentile(X_train.logerror.values, 2) # Filter the outliers from the dataframe
data[‘target’].loc[X_train[‘target’]>upper_limit] = upper_limit data[‘target’].loc[X_train[‘target’]<lower_limit] = lower_limit

Answer 15

a full example with data and 2 groups follows:

Imports:

from StringIO import StringIO
import pandas as pd
#pandas config
pd.set_option('display.max_rows', 20)

Data example with 2 groups: G1:Group 1. G2: Group 2:

TESTDATA = StringIO("""G1;G2;Value
1;A;1.6
1;A;5.1
1;A;7.1
1;A;8.1

1;B;21.1
1;B;22.1
1;B;24.1
1;B;30.6

2;A;40.6
2;A;51.1
2;A;52.1
2;A;60.6

2;B;80.1
2;B;70.6
2;B;90.6
2;B;85.1
""")

Read text data to pandas dataframe:

df = pd.read_csv(TESTDATA, sep=";")

Define the outliers using standard deviations

stds = 1.0
outliers = df[['G1', 'G2', 'Value']].groupby(['G1','G2']).transform(
           lambda group: (group - group.mean()).abs().div(group.std())) > stds

Define filtered data values and the outliers:

dfv = df[outliers.Value == False]
dfo = df[outliers.Value == True]

Print the result:

print '\n'*5, 'All values with decimal 1 are non-outliers. In the other hand, all values with 6 in the decimal are.'
print '\nDef DATA:\n%s\n\nFiltred Values with %s stds:\n%s\n\nOutliers:\n%s' %(df, stds, dfv, dfo)

Answer 16

My function for dropping outliers

def drop_outliers(df, field_name):
    distance = 1.5 * (np.percentile(df[field_name], 75) - np.percentile(df[field_name], 25))
    df.drop(df[df[field_name] > distance + np.percentile(df[field_name], 75)].index, inplace=True)
    df.drop(df[df[field_name] < np.percentile(df[field_name], 25) - distance].index, inplace=True)

Answer 17

I prefer to clip rather than drop. the following will clip inplace at the 2nd and 98th pecentiles.

df_list = list(df)
minPercentile = 0.02
maxPercentile = 0.98

for _ in range(numCols):
    df[df_list[_]] = df[df_list[_]].clip((df[df_list[_]].quantile(minPercentile)),(df[df_list[_]].quantile(maxPercentile)))

Answer 18

Deleting and dropping outliers I believe is wrong statistically. It makes the data different from original data. Also makes data unequally shaped and hence best way is to reduce or avoid the effect of outliers by log transform the data. This worked for me:

np.log(data.iloc[:, :])