An algorithm for inflating/deflating (offsetting, buffering) polygons

Question

How would I "inflate" a polygon? That is, I want to do something similar to this:

The requirement is that the new (inflated) polygon's edges/points are all at the same constant distance from the old (original) polygon's (on the example picture they are not, since then it would have to use arcs for inflated vertices, but let's forget about that for now ;) ).

The mathematical term for what I'm looking for is actually inward/outward polygon offseting. +1 to balint for pointing this out. The alternative naming is polygon buffering.

Results of my search:

Here are some links:

• A Survey of Polygon Offseting Strategies
• Polygon offset, PROBLEM
• Buffering Polygon Data

Answer 1

I thought I might briefly mention my own polygon clipping and offsetting library - Clipper.

While Clipper is primarily designed for polygon clipping operations, it does polygon offsetting too. The library is open source freeware written in Delphi, C++ and C#. It has a very unencumbered Boost license allowing it to be used in both freeware and commercial applications without charge.

Polygon offsetting can be performed using one of three offset styles - squared, round and mitered.

August 2022:
Clipper2 has now been formally released and it supercedes Clipper (aka Clipper1).

Answer 2

The polygon you are looking for is called inward/outward offset polygon in computational geometry and it is closely related to the straight skeleton.

These are several offset polygons for a complicated polygon:

And this is the straight skeleton for another polygon:

As pointed out in other comments, as well, depending on how far you plan to "inflate/deflate" your polygon you can end up with different connectivity for the output.

From computation point of view: once you have the straight skeleton one should be able to construct the offset polygons relatively easily. The open source and (free for non-commercial) CGAL library has a package implementing these structures. See this code example to compute offset polygons using CGAL.

The package manual should give you a good starting point on how to construct these structures even if you are not going to use CGAL, and contains references to the papers with the mathematical definitions and properties:

CGAL manual: 2D Straight Skeleton and Polygon Offsetting

Answer 3

For these types of things I usually use JTS. For demonstration purposes I created this jsFiddle that uses JSTS (JavaScript port of JTS). You just need to convert the coordinates you have to JSTS coordinates:

function vectorCoordinates2JTS (polygon) {
  var coordinates = [];
  for (var i = 0; i < polygon.length; i++) {
    coordinates.push(new jsts.geom.Coordinate(polygon[i].x, polygon[i].y));
  }
  return coordinates;
}

The result is something like this:

Additional info: I usually use this type of inflating/deflating (a little modified for my purposes) for setting boundaries with radius on polygons that are drawn on a map (with Leaflet or Google maps). You just convert (lat,lng) pairs to JSTS coordinates and everything else is the same. Example:

Answer 4

Sounds to me like what you want is:

• Starting at a vertex, face anti-clockwise along an adjacent edge.
• Replace the edge with a new, parallel edge placed at distance d to the "left" of the old one.
• Repeat for all edges.
• Find the intersections of the new edges to get the new vertices.
• Detect if you've become a crossed polygon and decide what to do about it. Probably add a new vertex at the crossing-point and get rid of some old ones. I'm not sure whether there's a better way to detect this than just to compare every pair of non-adjacent edges to see if their intersection lies between both pairs of vertices.

The resulting polygon lies at the required distance from the old polygon "far enough" from the vertices. Near a vertex, the set of points at distance d from the old polygon is, as you say, not a polygon, so the requirement as stated cannot be fulfilled.

I don't know if this algorithm has a name, example code on the web, or a fiendish optimisation, but I think it describes what you want.

Answer 5

In the GIS world one uses negative buffering for this task: http://www-users.cs.umn.edu/~npramod/enc_pdf.pdf

The JTS library should do this for you. See the documentation for the buffer operation: http://tsusiatsoftware.net/jts/javadoc/com/vividsolutions/jts/operation/buffer/package-summary.html

For a rough overview see also the Developer Guide: http://www.vividsolutions.com/jts/bin/JTS%20Developer%20Guide.pdf

Answer 6

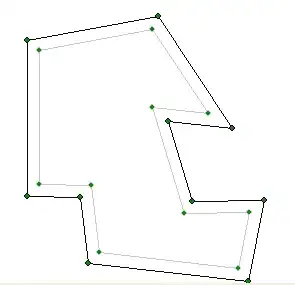
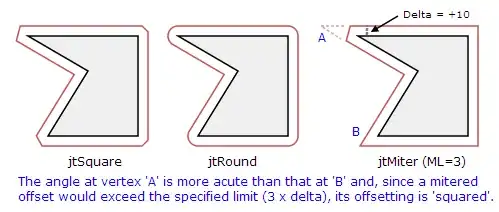
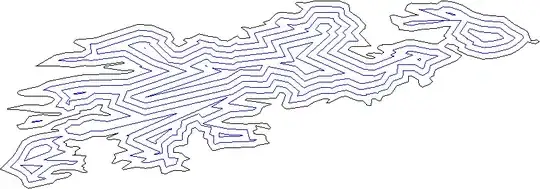
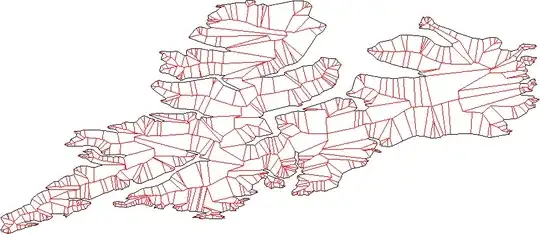
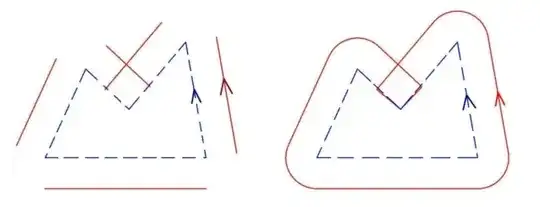
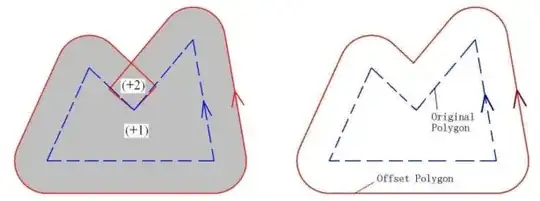
Each line should split the plane to "inside" and "outline"; you can find this out using the usual inner-product method.

Move all lines outward by some distance.

Consider all pair of neighbor lines (lines, not line segment), find the intersection. These are the new vertex.

Cleanup the new vertex by removing any intersecting parts. -- we have a few case here

(a) Case 1:

 0--7  4--3
 |  |  |  |
 |  6--5  |
 |        |
 1--------2

if you expend it by one, you got this:

0----a----3
|    |    |
|    |    |
|    b    |
|         |
|         |
1---------2

7 and 4 overlap.. if you see this, you remove this point and all points in between.

(b) case 2

 0--7  4--3
 |  |  |  |
 |  6--5  |
 |        |
 1--------2

if you expend it by two, you got this:

0----47----3
|    ||    |
|    ||    |
|    ||    |
|    56    |
|          |
|          |
|          |
1----------2

to resolve this, for each segment of line, you have to check if it overlap with latter segments.

(c) case 3

       4--3
 0--X9 |  |
 |  78 |  |
 |  6--5  |
 |        |
 1--------2

expend by 1. this is a more general case for case 1.

(d) case 4

same as case3, but expend by two.

Actually, if you can handle case 4. All other cases are just special case of it with some line or vertex overlapping.

To do case 4, you keep a stack of vertex.. you push when you find lines overlapping with latter line, pop it when you get the latter line. -- just like what you do in convex-hull.

Answer 7

Here is an alternative solution, see if you like this better.

1. Do a triangulation, it don't have to be delaunay -- any triangulation would do.

2. Inflate each triangle -- this should be trivial. if you store the triangle in the anti-clockwise order, just move the lines to right-hand-side and do intersection.

3. Merge them using a modified Weiler-Atherton clipping algorithm

Answer 8

Big thanks to Angus Johnson for his clipper library. There are good code samples for doing the clipping stuff at the clipper homepage at http://www.angusj.com/delphi/clipper.php#code but I did not see an example for polygon offsetting. So I thought that maybe it is of use for someone if I post my code:

    public static List<Point> GetOffsetPolygon(List<Point> originalPath, double offset)
    {
        List<Point> resultOffsetPath = new List<Point>();

        List<ClipperLib.IntPoint> polygon = new List<ClipperLib.IntPoint>();
        foreach (var point in originalPath)
        {
            polygon.Add(new ClipperLib.IntPoint(point.X, point.Y));
        }

        ClipperLib.ClipperOffset co = new ClipperLib.ClipperOffset();
        co.AddPath(polygon, ClipperLib.JoinType.jtRound, ClipperLib.EndType.etClosedPolygon);

        List<List<ClipperLib.IntPoint>> solution = new List<List<ClipperLib.IntPoint>>();
        co.Execute(ref solution, offset);

        foreach (var offsetPath in solution)
        {
            foreach (var offsetPathPoint in offsetPath)
            {
                resultOffsetPath.Add(new Point(Convert.ToInt32(offsetPathPoint.X), Convert.ToInt32(offsetPathPoint.Y)));
            }
        }

        return resultOffsetPath;
    }

Answer 9

One further option is to use boost::polygon - the documentation is somewhat lacking, but you should find that the methods resize and bloat, and also the overloaded += operator, which actually implement buffering. So for example increasing the size of a polygon (or a set of polygons) by some value can be as simple as:

poly += 2; // buffer polygon by 2

Answer 10

Based on advice from @JoshO'Brian, it appears the rGeos package in the R language implements this algorithm. See rGeos::gBuffer .

Answer 11

I use simple geometry: Vectors and/or Trigonometry

1. At each corner find the mid vector, and mid angle. Mid vector is the arithmetic average of the two unit vectors defined by the edges of the corner. Mid Angle is the half of the angle defined by the edges.

2. If you need to expand (or contract) your polygon by the amount of d from each edge; you should go out (in) by the amount d/sin(midAngle) to get the new corner point.

3. Repeat this for all the corners

*** Be careful about your direction. Make CounterClockWise Test using the three points defining the corner; to find out which way is out, or in.

Answer 12

There are a couple of libraries one can use (Also usable for 3D data sets).

1. https://github.com/otherlab/openmesh
2. https://github.com/alecjacobson/nested_cages
3. http://homepage.tudelft.nl/h05k3/Projects/MeshThickeningProj.htm

One can also find corresponding publications for these libraries to understand the algorithms in more detail.

The last one has the least dependencies and is self-contained and can read in .obj files.

Answer 13

This is a C# implementation of the algorithm explained in here . It is using Unity math library and collection package as well.

public static NativeArray<float2> ExpandPoly(NativeArray<float2> oldPoints, float offset, int outer_ccw = 1)
{
    int num_points = oldPoints.Length;
    NativeArray<float2> newPoints = new NativeArray<float2>(num_points, Allocator.Temp);

    for (int curr = 0; curr < num_points; curr++)
    {
        int prev = (curr + num_points - 1) % num_points;
        int next = (curr + 1) % num_points;

        float2 vn = oldPoints[next] - oldPoints[curr];
        float2 vnn = math.normalize(vn);
        float nnnX = vnn.y;
        float nnnY = -vnn.x;

        float2 vp = oldPoints[curr] - oldPoints[prev];
        float2 vpn = math.normalize(vp);
        float npnX = vpn.y * outer_ccw;
        float npnY = -vpn.x * outer_ccw;

        float bisX = (nnnX + npnX) * outer_ccw;
        float bisY = (nnnY + npnY) * outer_ccw;

        float2 bisn = math.normalize(new float2(bisX, bisY));
        float bislen = offset / math.sqrt((1 + nnnX * npnX + nnnY * npnY) / 2);

        newPoints[curr] = new float2(oldPoints[curr].x + bislen * bisn.x, oldPoints[curr].y + bislen * bisn.y);
    }

    return newPoints;
}

Answer 14

Thanks for the help in this topic, here's the code in C++ if anyone interested. Tested it, its working. If you give offset = -1.5, it will shrink the polygon.

    typedef struct {
        double x;
        double y;
    } Point2D;
    
    double Hypot(double x, double y)
    {
        return std::sqrt(x * x + y * y);
    }
    
    Point2D NormalizeVector(const Point2D& p)
    {
        double h = Hypot(p.x, p.y);
        if (h < 0.0001)
            return Point2D({ 0.0, 0.0 });
    
        double inverseHypot = 1 / h;
        return Point2D({ (double)p.x * inverseHypot, (double)p.y * inverseHypot });
    }
    
    void offsetPolygon(std::vector<Point2D>& polyCoords, std::vector<Point2D>& newPolyCoords, double offset, int outer_ccw)
    {
        if (offset == 0.0 || polyCoords.size() < 3)
            return;
    
        Point2D vnn, vpn, bisn;
        double vnX, vnY, vpX, vpY;
        double nnnX, nnnY;
        double npnX, npnY;
        double bisX, bisY, bisLen;
    
        unsigned int nVerts = polyCoords.size() - 1;
    
        for (unsigned int curr = 0; curr < polyCoords.size(); curr++)
        {
            int prev = (curr + nVerts - 1) % nVerts;
            int next = (curr + 1) % nVerts;
    
            vnX = polyCoords[next].x - polyCoords[curr].x;
            vnY = polyCoords[next].y - polyCoords[curr].y;
            vnn = NormalizeVector({ vnX, vnY });
            nnnX = vnn.y;
            nnnY = -vnn.x;
    
            vpX = polyCoords[curr].x - polyCoords[prev].x;
            vpY = polyCoords[curr].y - polyCoords[prev].y;
            vpn = NormalizeVector({ vpX, vpY });
            npnX = vpn.y * outer_ccw;
            npnY = -vpn.x * outer_ccw;
    
            bisX = (nnnX + npnX) * outer_ccw;
            bisY = (nnnY + npnY) * outer_ccw;
    
            bisn = NormalizeVector({ bisX, bisY });
            bisLen = offset / std::sqrt((1 + nnnX * npnX + nnnY * npnY) / 2);
    
            newPolyCoords.push_back({ polyCoords[curr].x + bisLen * bisn.x, polyCoords[curr].y + bisLen * bisn.y });
        }
    }

Answer 15

To inflate a polygon, one can implement the algorithm from "Polygon Offsetting by Computing Winding Numbers" article.

The steps of the algorithm are as follows:

1. Construct outer offset curve by taking every edge from input polygon and shifting it outside, then connecting shifted edged with circular arches in convex vertices of input polygon and two line segments in concave vertices of input polygon.

An example. Here input polygon is dashed blue, and red on the left - shifted edges, on the right - after connecting them in continuous self-intersecting curve:

2. The curve divides the plane on a number of connected components, and one has to compute the winding number in each of them, then take the boundary of all connected components with positive winding numbers:

The article proofs that the algorithm is very fast compared to competitors and robust at the same time.

To avoid implementing winding number computation, one can pass self-intersecting offset curve to OpenGL Utility library (GLU) tessellator and activate the settings GLU_TESS_BOUNDARY_ONLY=GL_TRUE (to skip triangulation) and GLU_TESS_WINDING_RULE=GLU_TESS_WINDING_POSITIVE (to output the boundary of positive winding number components).