Finding local maxima/minima with Numpy in a 1D numpy array

Question

Can you suggest a module function from numpy/scipy that can find local maxima/minima in a 1D numpy array? Obviously the simplest approach ever is to have a look at the nearest neighbours, but I would like to have an accepted solution that is part of the numpy distro.

Answer 1

In SciPy >= 0.11

import numpy as np
from scipy.signal import argrelextrema

x = np.random.random(12)

# for local maxima
argrelextrema(x, np.greater)

# for local minima
argrelextrema(x, np.less)

Produces

>>> x
array([ 0.56660112,  0.76309473,  0.69597908,  0.38260156,  0.24346445,
    0.56021785,  0.24109326,  0.41884061,  0.35461957,  0.54398472,
    0.59572658,  0.92377974])
>>> argrelextrema(x, np.greater)
(array([1, 5, 7]),)
>>> argrelextrema(x, np.less)
(array([4, 6, 8]),)

Note, these are the indices of x that are local max/min. To get the values, try:

>>> x[argrelextrema(x, np.greater)[0]]

scipy.signal also provides argrelmax and argrelmin for finding maxima and minima respectively.

Answer 2

If you are looking for all entries in the 1d array a smaller than their neighbors, you can try

numpy.r_[True, a[1:] < a[:-1]] & numpy.r_[a[:-1] < a[1:], True]

You could also smooth your array before this step using numpy.convolve().

I don't think there is a dedicated function for this.

Answer 3

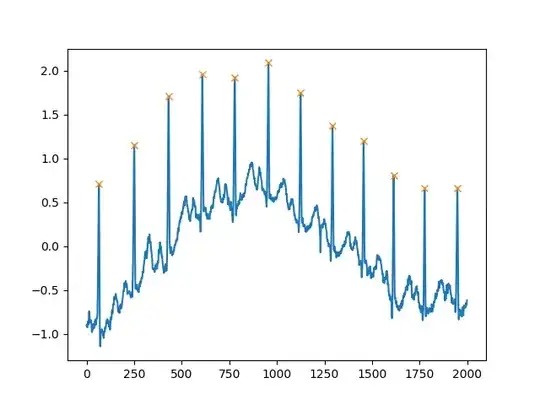
As of SciPy version 1.1, you can also use find_peaks. Below are two examples taken from the documentation itself.

Using the height argument, one can select all maxima above a certain threshold (in this example, all non-negative maxima; this can be very useful if one has to deal with a noisy baseline; if you want to find minima, just multiply you input by -1):

import matplotlib.pyplot as plt
from scipy.misc import electrocardiogram
from scipy.signal import find_peaks
import numpy as np

x = electrocardiogram()[2000:4000]
peaks, _ = find_peaks(x, height=0)
plt.plot(x)
plt.plot(peaks, x[peaks], "x")
plt.plot(np.zeros_like(x), "--", color="gray")
plt.show()

Another extremely helpful argument is distance, which defines the minimum distance between two peaks:

peaks, _ = find_peaks(x, distance=150)
# difference between peaks is >= 150
print(np.diff(peaks))
# prints [186 180 177 171 177 169 167 164 158 162 172]

plt.plot(x)
plt.plot(peaks, x[peaks], "x")
plt.show()

Answer 4

For curves with not too much noise, I recommend the following small code snippet:

from numpy import *

# example data with some peaks:
x = linspace(0,4,1e3)
data = .2*sin(10*x)+ exp(-abs(2-x)**2)

# that's the line, you need:
a = diff(sign(diff(data))).nonzero()[0] + 1 # local min+max
b = (diff(sign(diff(data))) > 0).nonzero()[0] + 1 # local min
c = (diff(sign(diff(data))) < 0).nonzero()[0] + 1 # local max


# graphical output...
from pylab import *
plot(x,data)
plot(x[b], data[b], "o", label="min")
plot(x[c], data[c], "o", label="max")
legend()
show()

The +1 is important, because diff reduces the original index number.

Answer 5

Another approach (more words, less code) that may help:

The locations of local maxima and minima are also the locations of the zero crossings of the first derivative. It is generally much easier to find zero crossings than it is to directly find local maxima and minima.

Unfortunately, the first derivative tends to "amplify" noise, so when significant noise is present in the original data, the first derivative is best used only after the original data has had some degree of smoothing applied.

Since smoothing is, in the simplest sense, a low pass filter, the smoothing is often best (well, most easily) done by using a convolution kernel, and "shaping" that kernel can provide a surprising amount of feature-preserving/enhancing capability. The process of finding an optimal kernel can be automated using a variety of means, but the best may be simple brute force (plenty fast for finding small kernels). A good kernel will (as intended) massively distort the original data, but it will NOT affect the location of the peaks/valleys of interest.

Fortunately, quite often a suitable kernel can be created via a simple SWAG ("educated guess"). The width of the smoothing kernel should be a little wider than the widest expected "interesting" peak in the original data, and its shape will resemble that peak (a single-scaled wavelet). For mean-preserving kernels (what any good smoothing filter should be) the sum of the kernel elements should be precisely equal to 1.00, and the kernel should be symmetric about its center (meaning it will have an odd number of elements.

Given an optimal smoothing kernel (or a small number of kernels optimized for different data content), the degree of smoothing becomes a scaling factor for (the "gain" of) the convolution kernel.

Determining the "correct" (optimal) degree of smoothing (convolution kernel gain) can even be automated: Compare the standard deviation of the first derivative data with the standard deviation of the smoothed data. How the ratio of the two standard deviations changes with changes in the degree of smoothing cam be used to predict effective smoothing values. A few manual data runs (that are truly representative) should be all that's needed.

All the prior solutions posted above compute the first derivative, but they don't treat it as a statistical measure, nor do the above solutions attempt to performing feature preserving/enhancing smoothing (to help subtle peaks "leap above" the noise).

Finally, the bad news: Finding "real" peaks becomes a royal pain when the noise also has features that look like real peaks (overlapping bandwidth). The next more-complex solution is generally to use a longer convolution kernel (a "wider kernel aperture") that takes into account the relationship between adjacent "real" peaks (such as minimum or maximum rates for peak occurrence), or to use multiple convolution passes using kernels having different widths (but only if it is faster: it is a fundamental mathematical truth that linear convolutions performed in sequence can always be convolved together into a single convolution). But it is often far easier to first find a sequence of useful kernels (of varying widths) and convolve them together than it is to directly find the final kernel in a single step.

Hopefully this provides enough info to let Google (and perhaps a good stats text) fill in the gaps. I really wish I had the time to provide a worked example, or a link to one. If anyone comes across one online, please post it here!

Answer 6

I believe there is a much simpler approach in numpy (a one liner).

import numpy as np

list = [1,3,9,5,2,5,6,9,7]

np.diff(np.sign(np.diff(list))) #the one liner

#output
array([ 0, -2,  0,  2,  0,  0, -2])

To find a local max or min we essentially want to find when the difference between the values in the list (3-1, 9-3...) changes from positive to negative (max) or negative to positive (min). Therefore, first we find the difference. Then we find the sign, and then we find the changes in sign by taking the difference again. (Sort of like a first and second derivative in calculus, only we have discrete data and don't have a continuous function.)

The output in my example does not contain the extrema (the first and last values in the list). Also, just like calculus, if the second derivative is negative, you have max, and if it is positive you have a min.

Thus we have the following matchup:

[1,  3,  9,  5,  2,  5,  6,  9,  7]
    [0, -2,  0,  2,  0,  0, -2]
        Max     Min         Max

Answer 7

Why not use Scipy built-in function signal.find_peaks_cwt to do the job ?

from scipy import signal
import numpy as np

#generate junk data (numpy 1D arr)
xs = np.arange(0, np.pi, 0.05)
data = np.sin(xs)

# maxima : use builtin function to find (max) peaks
max_peakind = signal.find_peaks_cwt(data, np.arange(1,10))

# inverse  (in order to find minima)
inv_data = 1/data
# minima : use builtin function fo find (min) peaks (use inversed data)
min_peakind = signal.find_peaks_cwt(inv_data, np.arange(1,10))

#show results
print "maxima",  data[max_peakind]
print "minima",  data[min_peakind]

results:

maxima [ 0.9995736]
minima [ 0.09146464]

Regards

Answer 8

Update: I wasn't happy with gradient so I found it more reliable to use numpy.diff.

Regarding the issue of noise, the mathematical problem is to locate maxima/minima if we want to look at noise we can use something like convolve which was mentioned earlier.

import numpy as np
from matplotlib import pyplot

a=np.array([10.3,2,0.9,4,5,6,7,34,2,5,25,3,-26,-20,-29],dtype=np.float)

gradients=np.diff(a)
print gradients


maxima_num=0
minima_num=0
max_locations=[]
min_locations=[]
count=0
for i in gradients[:-1]:
        count+=1

    if ((cmp(i,0)>0) & (cmp(gradients[count],0)<0) & (i != gradients[count])):
        maxima_num+=1
        max_locations.append(count)     

    if ((cmp(i,0)<0) & (cmp(gradients[count],0)>0) & (i != gradients[count])):
        minima_num+=1
        min_locations.append(count)


turning_points = {'maxima_number':maxima_num,'minima_number':minima_num,'maxima_locations':max_locations,'minima_locations':min_locations}  

print turning_points

pyplot.plot(a)
pyplot.show()

Answer 9

None of these solutions worked for me since I wanted to find peaks in the center of repeating values as well. for example, in

ar = np.array([0,1,2,2,2,1,3,3,3,2,5,0])

the answer should be

array([ 3,  7, 10], dtype=int64)

I did this using a loop. I know it's not super clean, but it gets the job done.

def findLocalMaxima(ar):
# find local maxima of array, including centers of repeating elements    
maxInd = np.zeros_like(ar)
peakVar = -np.inf
i = -1
while i < len(ar)-1:
#for i in range(len(ar)):
    i += 1
    if peakVar < ar[i]:
        peakVar = ar[i]
        for j in range(i,len(ar)):
            if peakVar < ar[j]:
                break
            elif peakVar == ar[j]:
                continue
            elif peakVar > ar[j]:
                peakInd = i + np.floor(abs(i-j)/2)
                maxInd[peakInd.astype(int)] = 1
                i = j
                break
    peakVar = ar[i]
maxInd = np.where(maxInd)[0]
return maxInd 

Answer 10

import numpy as np
x=np.array([6,3,5,2,1,4,9,7,8])
y=np.array([2,1,3,5,3,9,8,10,7])
sortId=np.argsort(x)
x=x[sortId]
y=y[sortId]
minm = np.array([])
maxm = np.array([])
i = 0
while i < length-1:
    if i < length - 1:
        while i < length-1 and y[i+1] >= y[i]:
            i+=1

        if i != 0 and i < length-1:
            maxm = np.append(maxm,i)

        i+=1

    if i < length - 1:
        while i < length-1 and y[i+1] <= y[i]:
            i+=1

        if i < length-1:
            minm = np.append(minm,i)
        i+=1


print minm
print maxm

minm and maxm contain indices of minima and maxima, respectively. For a huge data set, it will give lots of maximas/minimas so in that case smooth the curve first and then apply this algorithm.

Answer 11

Another solution using essentially a dilate operator:

import numpy as np
from scipy.ndimage import rank_filter

def find_local_maxima(x):
   x_dilate = rank_filter(x, -1, size=3)
   return x_dilate == x

and for the minima:

def find_local_minima(x):
   x_erode = rank_filter(x, -0, size=3)
   return x_erode == x

Also, from scipy.ndimage you can replace rank_filter(x, -1, size=3) with grey_dilation and rank_filter(x, 0, size=3) with grey_erosion. This won't require a local sort, so it is slightly faster.

Answer 12

Another one:

def local_maxima_mask(vec):
    """
    Get a mask of all points in vec which are local maxima
    :param vec: A real-valued vector
    :return: A boolean mask of the same size where True elements correspond to maxima. 
    """
    mask = np.zeros(vec.shape, dtype=np.bool)
    greater_than_the_last = np.diff(vec)>0  # N-1
    mask[1:] = greater_than_the_last
    mask[:-1] &= ~greater_than_the_last
    return mask

Answer 13

And ... yet another answer.

This one requires NO extra packages (except numpy). For example,

points = [ 0, 0, 1, 2, 3, 3, 2, 2, 3, 1, 1 ]
minimums   ^  ^              ^  ^     ^  ^

will return a list of all the local minima

result = [ 0, 1, 6, 7, 9, 10 ]

it could easily be extended to also look for maxima.

def find_valleys(points: np.ndarray, edges=True) -> list:
    """
    Find the indices of all points that are local minimums.

    :param np.ndarray points: a 1D array of numeric data
    :param bool edges: allows the first and last indices to be returned, defaults to True
    :return list: a list of integers, indices into the array
    """
    dif = np.diff(points)
    p = -1 if edges else 1
    s = 0
    result = []
    for i,d in enumerate(dif):
        if d < 0: s = i + 1
        if p < 0 and d > 0:   # found a valley
            result.extend(range(s,i + 1))
        if d: p = d
    if p < 0 and edges:
        result.extend(range(s,i + 2))
    return result